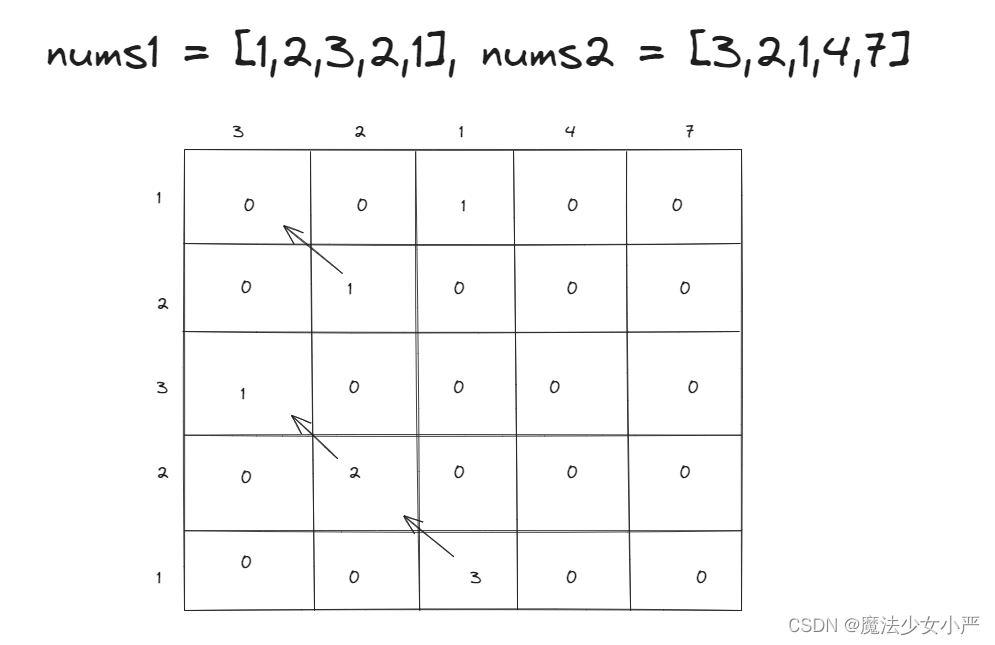
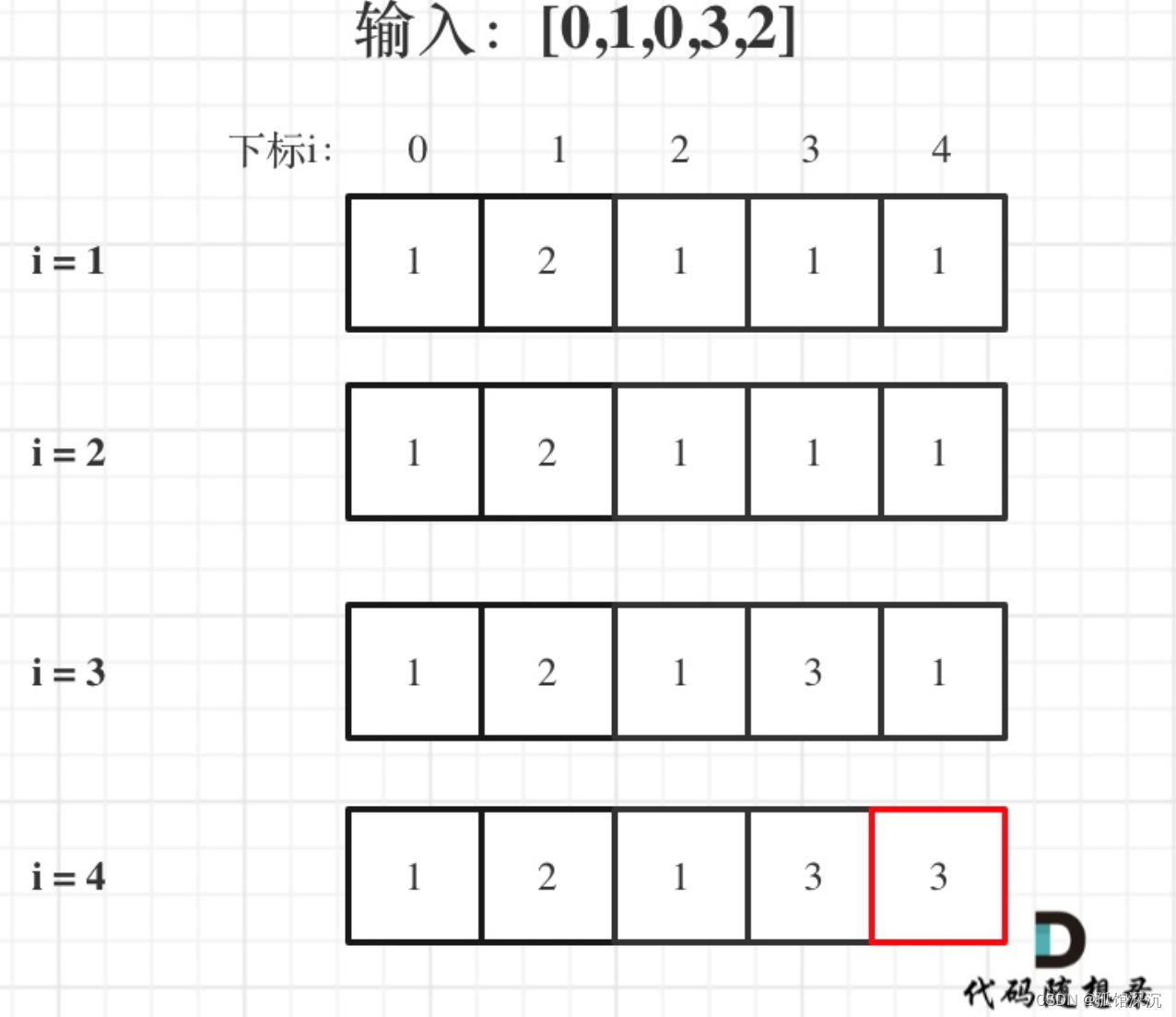
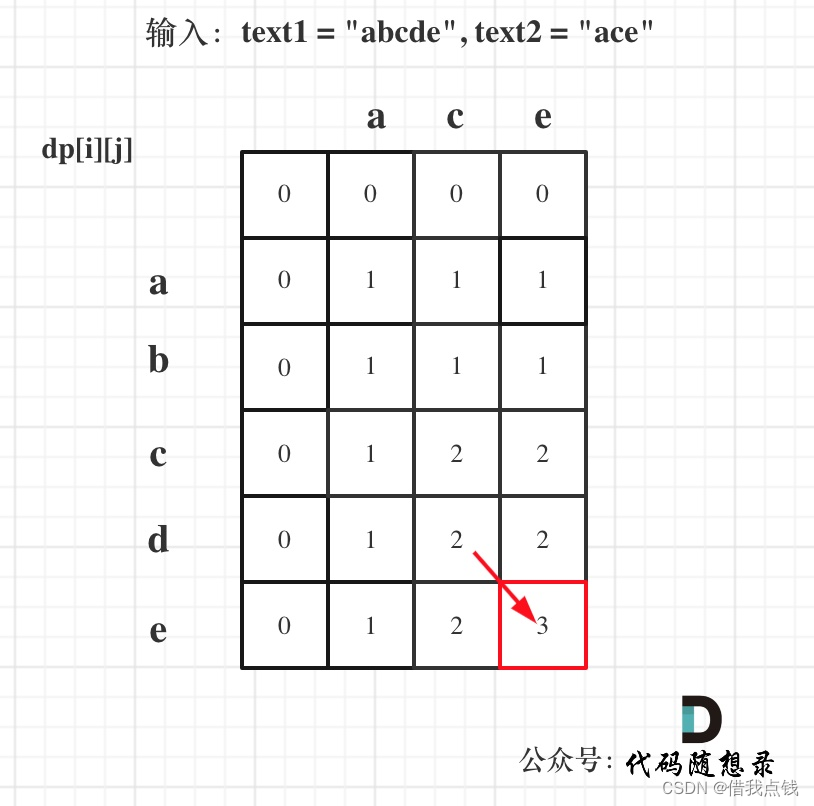
674专题
674 - Coin Change
一道很水的DP,但我做的时候也很费劲,由于存在面值为1的时候,所以所有面额都至少有1种方法。 推导出状态方程就是 dp(V,step) += dp(V - i * coin[step],step - 1); 其中V为当前的面值,coin[step]为硬币的面额,递归边界,如果step == 0(也就是递归到硬币面额为1的时候,返回1); #include<cstdio>#include<
代码随想录算法训练营四十二天|300.最长递增子序列、674.最长连续递增则序列、718.最长重复子数组
题目链接:300. 最长递增子序列 - 力扣(LeetCode) 思路:如果nums[i] > nums[j] 那么dp[i] 要么是dp[i] 要么是dp[j] + 1 class Solution(object):def lengthOfLIS(self, nums):""":type nums: List[int]:rtype: int"""dp = [1] * len(nums)for
leetcode第674题,Longest Continuous Increasing Subsequence
第674题,Longest Continuous Increasing Subsequence 题目: Given an unsorted array of integers, find the length of longest continuous increasing subsequence (subarray). 本题的意思是给一个未排序的数组,求出数组中连续递增的序列的最大长度。
第五十天 进入子序列问题 | 300.最长递增子序列 674.最长连续递增序列 718.最长重复子数组
题目:300.最长递增子序列 1.dp数组的定义: 以nums[i]为结尾的最长递增子序列的长度 为什么一定表示 “以nums[i]结尾的最长递增子序” ,因为我们在 做 递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾, 要不然这个比较就没有意义了,不是尾部元素的比较那么 如何算
代码随想录算法训练营Day51 | 300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组
代码随想录算法训练营Day51 | 300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组 LeetCode 300.最长递增子序列 题目链接:LeetCode 300.最长递增子序列 思路: 选取最长子序列,并收集 class Solution {public:int lengthOfLIS(vector<int>& nums) {int n = nums.siz
【算法刷题day52】Leetcode:300. 最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
文章目录 Leetcode 300. 最长递增子序列解题思路代码总结 Leetcode 674. 最长连续递增序列解题思路代码总结 Leetcode 718. 最长重复子数组解题思路代码总结 草稿图网站 java的Deque Leetcode 300. 最长递增子序列 题目:300. 最长递增子序列 解析:代码随想录解析 解题思路 dp数组的含义是以该元素为结尾的
代码随想录算法训练营第五十二天|300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组
目录 300.最长递增子序列思路代码 674. 最长连续递增序列思路代码 718. 最长重复子数组思路代码 300.最长递增子序列 题目链接:300.最长递增子序列 文档讲解:代码随想录 视频讲解:动态规划之子序列问题,元素不连续!| LeetCode:300.最长递增子序列 思路 dp数组dp[i]表示i(包括i)以内的以nums[i]结尾的最长递增子序列的长度。
代码随想录算法训练营DAY50|C++动态规划Part11|300.最长递增子序列、674.最长连续递增序列、718.最长重复子数组
文章目录 300.最长递增子序列思路CPP代码 674.最长连续递增序列思路CPP代码 718.最长重复子数组思路CPP代码 300.最长递增子序列 力扣题目链接 文章讲解:300.最长递增子序列 视频链接:动态规划之子序列问题,元素不连续!| LeetCode:300.最长递增子序列 可以删除或不删除某些元素,保证数组原有的顺序,然后求最长的递增子序列。 这是典型的
Day51:动态规划 LeedCode 300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组
300. 最长递增子序列 中等 相关标签 相关企业 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的 子序列 。 示例 1: 输入:nums = [10,9,2,5,3,7,101,18]输出:4解释:最长
草稿代码随想录算法训练营第day52|300.最长递增子序列 、 674. 最长连续递增序列 、 718. 最长重复子数组
目录 300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组 300.最长递增子序列 力扣题目链接 (opens new window) 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2
代码随想录算法训练营Day52 ||leetCode 300.最长递增子序列 || 674. 最长连续递增序列 || 718. 最长重复子数组
300.最长递增子序列 class Solution {public:int lengthOfLIS(vector<int>& nums) {if (nums.size() <= 1) return nums.size();vector<int> dp(nums.size(), 1);int result = 0;for (int i = 1; i < nums.size(
【动态规划】代码随想录算法训练营第五十二天 |300.最长递增子序列, 674. 最长连续递增序列 ,718. 最长重复子数组 (待补充)
300.最长递增子序列 1、题目链接:. - 力扣(LeetCode) 2、文章讲解:代码随想录 3、题目: 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。 示例 1: 输入:nums = [10,9,2,5
力扣● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
● 300.最长递增子序列 1.dp数组含义。dp[i]:以nums[i]为结尾的递增子序列的最大长度。 注意一定是以nums[i]结尾,如果dp[i]定义错误的话,暴力也不知道咋整。 2.递推公式。这道题与背包的单词划分比较像,一个单层循环是弄不出来的,外层循环i,内层循环j。即当前下标i的递增子序列长度,其实和i之前的下表j的子序列长度有关系。准确的说,i的递增子序列长度就是由[0,i-
2021-12-28 674. 最长连续递增序列(动态规划)
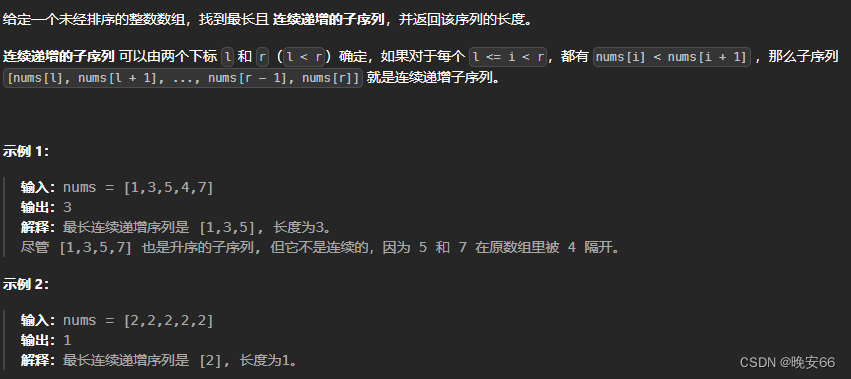
注: 题目: 给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。 连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。 示例 1: 输入:
LeetCode 第51天 | 300. 最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组 动态规划
300. 最长递增子序列 用当前值与之前的左右值比较,如果大于前面的值,那么就可以用前面的dp加上长度一(当前值本身长度)。就是前面的值大小记录下来,后面会用的到,到dp[i]的点记录了dp[i]之前的局部最长子序列,那么如果后续遍历到的值严格大于该值的话,就可以动态更新后面的值了。解决局部问题记录状态,解决全局问题就可以利用局部解的值来优化全局解。 class Solution {publi
代码随想录算法训练营第五十二天丨300. 最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
300. 最长递增子序列 动规: 妥妥O(n^2)的动规 dp[i]表示以i结尾的LIS,初始化都为1。 当nums[i + 1]加入进来,就要去找0-i中比nums[i + 1]小的nums[j], 并且更新dp[i+1]为dp[j] + 1和他自己较大的一个。 class Solution:def lengthOfLIS(self, nums: List[int]) -> int:n
代码随想录算法训练营Day52 | 300.最长递增子序列、674.最长连续递增序列、718.最长重复子数组
300.最长递增子序列 这题的重点是DP数组的定义,子序列必须以nums[i]为最后一个元素,这样dp数组中后面的元素才能与前面的元素进行对比 1、DP数组定义:dp[i]表示以nums[i]为最后一个元素的最长递增子序列长度 2、DP数组初始化:全部初始化为1(子序列最少也有自身一个) 3、递推公式:与 i 前所有元素进行对比,如果nums[i] > nums[j],那么更新dp[i]
【LeetCode】674. 最长连续递增序列(简单)——代码随想录算法训练营Day52
题目链接: 题目描述 给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。 连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。 示例
代码随想录算法训练营Day52|300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
300.最长递增子序列 题目链接:300.最长递增子序列 文档链接:300.最长递增子序列 视频链接:动态规划之子序列问题,元素不连续!| LeetCode:300.最长递增子序列 C++实现 class Solution {public:int lengthOfLIS(vector<int>& nums) {if(nums.size() <= 1) return nums.size
【LeetCode-674】最长连续递增序列(动归)
目录 LeetCode674.最长连续递增序列 题目描述 解法1:动态规划 代码实现 题目链接 题目描述 给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。 连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], num
代码随想录算法训练营第55天 | 300.最长递增子序列 + 674.最长连续递增序列 + 718.最长重复子数组
今日任务 300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组 300.最长递增子序列 - Medium 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,
代码随想录算法训练营第五十六天|300.最长递增子序列 , 674. 最长连续递增序列 ,718. 最长重复子数组
300.最长递增子序列 今天开始正式子序列系列,本题是比较简单的,感受感受一下子序列题目的思路。 视频讲解:动态规划之子序列问题,元素不连续!| LeetCode:300.最长递增子序列_哔哩哔哩_bilibili 代码随想录 class Solution {public int lengthOfLIS(int[] nums) {//1.dp[i]表示i之前包括i的以nums[i]结
Day46 300最长递增子序列 674最长连续递增子序列 718最长重复子数组 1143最长公共子序列
300 最长递增子序列 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。 本题利用两个循环,外层循环 i 和内层循环 j,dp【j】表示 i 之内最长递增子序列长度,如果nums【i】> nums【j】, 那么就让dp
【算法与数据结构】300、674、LeetCode最长递增子序列 最长连续递增序列
文章目录 一、300、最长递增子序列二、674、最长连续递增序列三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、300、最长递增子序列 思路分析: 第一步,动态数组的含义。 d p [ i ] dp[i] dp[i]代表 i i i之前包括以 i i i结尾的最长递增子序列的长度。我们在做递增比较的时
Codeforces Round #674 (Div. 3)A-F题解
Codeforces Round #674 (Div. 3)A-F题解 比赛链接:https://codeforces.com/contest/1426 A题 水题不写题解 #include<bits/stdc++.h>#define ll long long#define llINF 9223372036854775807#define IOS ios::sync_with_stdi