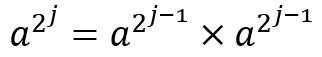骨牌专题
题目1 : 骨牌覆盖问题·一 (线性递推+矩阵快速幂)
题目来源 hiho一下 第四十一周 正在进行: 2天05小时28分钟25秒 首页 题目列表 我的提交 排名 讨论 报名人数:1264 题目1 : 骨牌覆盖问题·一 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 骨牌,一种古老的玩具。今天我们要研究的是骨牌的覆盖问题: 我们有一个2xN的长
寒假第五天--递推递归--骨牌铺方格
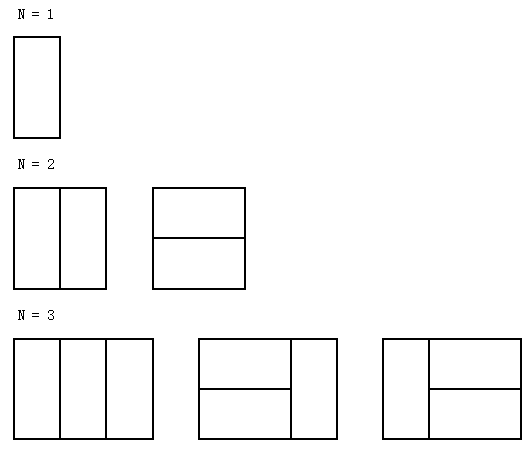
骨牌铺方格 Time Limit: 1000MS Memory limit: 32768K 题目描述 在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图: 输入 输入数据由多行组成,每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0< n<=50)。
SDUTOJ 1018 骨牌铺方格 递推
题目描述 在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图: 输入 输入数据由多行组成,每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0< n<=50)。 输出 对于每个测试实例,请输出铺放方案的总数,每个实例的输出占一行。 示例输入 132
HDU 2046骨牌铺方格
http://acm.hdu.edu.cn/showproblem.php?pid=2046 画图,找规律, 发现是: 斐波那契 注意类型用的是__int64, 输出格式:大写的i后面加上64d, __int64是2的63次方 - 1; longlong类型,输出格式是lld,小写的L; 使用递推的方法计算斐波那契数列; #include<stdio.h>#include<std
nyoj-429-骨牌铺方格//hdu-2046-骨牌铺方格
#include<stdio.h>//杭电上用long long过不了 int main() { int n,i; _int64 a[51]; a[0]=1; a[1]=2; a[2]=3; for(i=3;i<51;i++) a[i]=a[i-1]+a[i-2]; while(scanf("%d",&n)!=EOF) { printf("%I64d\n",
点头OJ 1033 . 骨牌覆盖 V2 ( 状态压缩 + 矩阵快速幂 )
题目链接~~> 做题感悟:先前做过一个类似的题,是俄罗斯的一道区域赛的题目,也是用的状态压缩 + 矩阵快速幂。 解题思路:状态压缩 + 矩阵快速幂 构造一个矩阵 B [ i ] [ j ] 代表状态 i ,与状态 j 是否合法,j 代表上一行的状态,如果合法为 1 ,否则为 0 ,这样如果再得到初始各种状态的方案数的矩阵 A ,A 只有一列 ,这样 B *
hihoCoder 1143 : 骨牌覆盖问题·一(递推,矩阵快速幂)
【题目链接】:click here~~ 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 骨牌,一种古老的玩具。今天我们要研究的是骨牌的覆盖问题: 我们有一个2xN的长条形棋盘,然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘,一共有多少种不同的覆盖方法呢? 举个例子,对于长度为1到3的棋盘,我们有下面几种覆盖方式:
铺瓷砖问题 HDU 2046 骨牌铺方格 + POJ 2663 Tri Tiling (递推)
骨牌铺方格 http://acm.hdu.edu.cn/showproblem.php?pid=2046 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Problem Description 在2×n的一个长方形方格中,用一个1×
骨牌铺方格 (sdut oj)
骨牌铺方格 Time Limit: 1000MS Memory Limit: 32768KB Problem Description 在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图: Input 输入数据由多行组成,每行包含一个
【hiho一下 第四十二周】骨牌覆盖问题·二
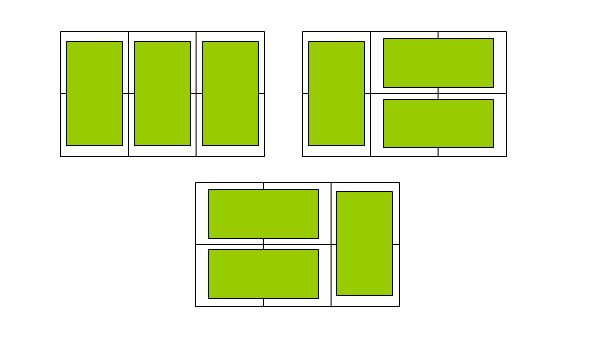
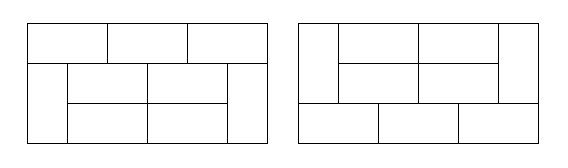
原题地址:http://hihocoder.com/contest/hiho42/problem/1 2xN的骨牌问题:http://blog.csdn.net/smile_watermelon/article/details/45151175 题目描述 上一周我们研究了2xN的骨牌问题,这一周我们不妨加大一下难度,研究一下3xN的骨牌问题? 所以我们的题目是:对于3xN的棋盘,使用1x2
【hiho一下 第四十一周】骨牌覆盖问题·一
原题地址:http://hihocoder.com/contest/hiho41/problem/1 题目描述 骨牌,一种古老的玩具。今天我们要研究的是骨牌的覆盖问题: 我们有一个2xN的长条形棋盘,然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘,一共有多少种不同的覆盖方法呢? 举个例子,对于长度为1到3的棋盘,我们有下面几种覆盖方式: 输入 第1行:1个整数N。表示棋盘
hihoCoder #1143 : 骨牌覆盖问题·一(矩阵乘法)
1143 : 骨牌覆盖问题·一 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 骨牌,一种古老的玩具。今天我们要研究的是骨牌的覆盖问题: 我们有一个2xN的长条形棋盘,然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘,一共有多少种不同的覆盖方法呢? 举个例子,对于长度为1到3的棋盘,我们有下面几种覆盖方式: week41_1.PNG 提示:骨牌覆盖
【SSL】1632骨牌游戏(多米诺骨牌)
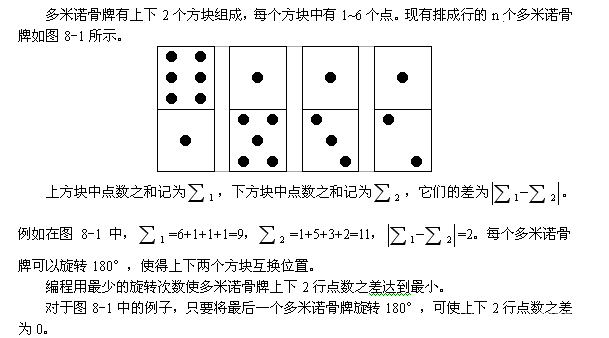
【SSL】1632骨牌游戏(多米诺骨牌) Time Limit:1000MS Memory Limit:65536K Description Input 输入文件的第一行是一个正整数n(1≤n≤1000),表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数,表示多米诺骨牌上下方块中的点数a和b,且1≤a,b≤6。 Output 输出文件仅一行,包
t2017递推3骨牌
答案: #include<iostream>using namespace std;long long n,s[10009];int main(){cin>>n;s[1]=1,s[2]=2,s[3]=4;if(n==1){cout<<1;return 0;}if(n==2){cout<<2;return 0;}if(n==3){cout<<4;return 0;}for(int i
puzzle(0411)《骨牌》覆盖、染色
目录 一,2格骨牌覆盖问题 1,剪残了的棋盘 2,算法谜题 12 平铺多米诺问题 二,3格骨牌覆盖问题 1,算法谜题 78 直三格板平铺 2,L骨牌覆盖问题 三,4-5格骨牌覆盖问题 1,算法谜题 38 四格骨牌平铺问题 2,智力游戏 打包1 3,智力游戏 打包2 4,智力游戏 打包3 5,日历拼图 6,立方体拼图 四,染色技巧 1,染色的本质 2,4格覆盖问题
HDU:2046骨牌铺方格nbsp;解题报告
斐波那契数列 #include<stdio.h> int main() { int n,i; __int64 a[55]; a[1]=1;a[2]=2; for(i=3;i<=51;i++) a[i]=a[i-1]+a[i-2]; while(scanf("%d",&n)!=EOF) printf("%I64d\n",a[n
HDU:2046骨牌铺方格nbsp;解题报告
斐波那契数列 #include<stdio.h> int main() { int n,i; __int64 a[55]; a[1]=1;a[2]=2; for(i=3;i<=51;i++) a[i]=a[i-1]+a[i-2]; while(scanf("%d",&n)!=EOF) printf("%I64d\n",a[n
HDU:2046骨牌铺方格解题报告
Fibnacci 数列: F(N)=F(N-1)+F(N-2);这个不解释! #include<stdio.h> int main() { int n,i; __int64 a[55]; a[1]=1;a[2]=2; for(i=3;i<=51;i++) a[i]=a[i-1]+a[i-2]; while(scanf("%d",&n)!=EOF) printf("%I64d\n
骨牌铺方格 2046
Problem Description 在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图: Input 输入数据由多行组成,每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。 Output 对于每个测试实例,请输出铺放方案的总数,每个实例的输出占一行。