L型骨牌覆盖问题。

本文主要是介绍L型骨牌覆盖问题。，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

问题：解决一个2k*2k的特殊棋牌上的L型骨牌覆盖问题。

思路：

棋盘覆盖实现的基本方法为分治法

当k=0时(1ⅹ1棋盘)，及特殊方格，骨牌数为0

当k >0时，将2kⅹ2k棋盘分割为4个2k-1ⅹ2k-1子棋盘了

特殊方格位于4个较小子棋盘之一中，而其余3个子棋盘中无特殊方格。

在递归之前要将原问题转化为4个较小规模的相同子问题。（用一个L型骨牌覆盖这3个子棋盘的会合处）

这三个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将问题分解为4个较小规模的棋盘覆盖问题。

递归地使用这种分割方法，直至棋盘简化为1ⅹ1棋盘，就结束递归。

具体实现

对每个子棋盘按照左上，右上，右下，左下的顺时针顺序铺满棋盘。（顺序不一样，铺出来的编号也不一样）

    每次都对分割后的四个小方块进行判断，判断特殊方格是否在里面。

如果特殊方块在里面，这直接递归下去即可，

    如果不在，这根据分割的四个方块的不同位置，把右下角、左下角、左上角、右上角的方格标记为特殊方块，然后继续递归。

    在递归函数里，还要有一个变量h来记录边的方格数，每次对方块进行划分时，边的方格数都会减半，这个变量是为了方便判断特殊方格的位置。

代码实现

x：棋盘左上角方格的行号

y：棋盘左上角方格的列号

a：特殊方格的行号

b：特殊方格的列号

length：2k，棋盘规模：2kⅹ2k

源码：

#include<iostream>#include<iomanip> using namespace std;int matrix[100][100];int num = 0;void chessBoard(int x, int y, int a, int b, int length);int main(){int a, b, length;cout << "请输入棋盘的行列号";cin >> length;cout << "请输入特殊方格的行列号";cin >> a >> b;matrix[a][b] = 0;chessBoard(1, 1, a, b, length);for (int i = 1; i <= length; i++) {for (int j = 1; j <= length; j++) {cout << setw(4) << matrix[i][j];}cout << endl;}system("pause");return 0;}void chessBoard(int x, int y, int a, int b, int length) {if (length == 1) {return;}int h = length / 2;  int t = ++num;       /*左上角*/if (a < x + h && b < y + h) { chessBoard(x, y, a, b, h);}else {  matrix[x + h - 1][y + h - 1] = t;chessBoard(x, y, x + h - 1, y + h - 1, h);}/*右上角*/if (a < x + h && b >= y + h) { chessBoard(x, y + h, a, b, h);}else { matrix[x + h - 1][y + h] = t;chessBoard(x, y + h, x + h - 1, y + h, h);}/*右下角*/if (a >= x + h && b >= y + h) { chessBoard(x + h, y + h, a, b, h);}else { matrix[x + h][y + h] = t;chessBoard(x + h, y + h, x + h, y + h, h);}/*左下角*/if (a >= x + h && b < y + h) { chessBoard(x + h, y, a, b, h);}else {  matrix[x + h][y + h - 1] = t;chessBoard(x + h, y, x + h, y + h - 1, h);}}

运行截图：

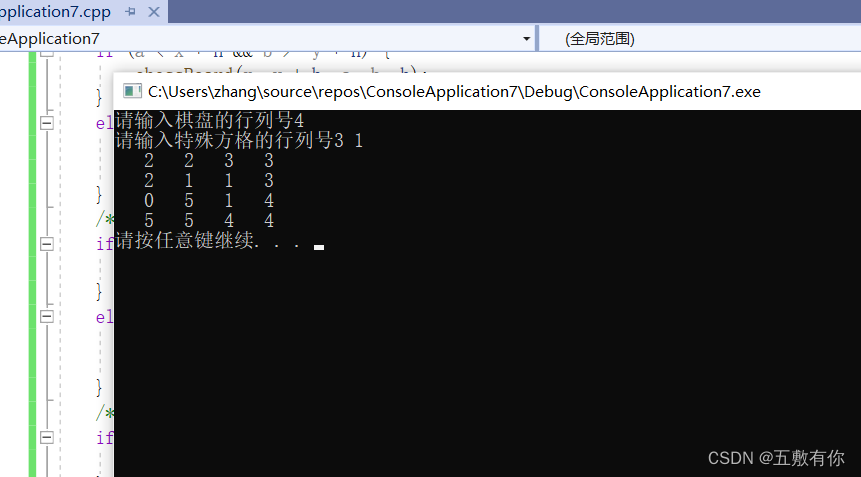
这篇关于L型骨牌覆盖问题。的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---