本文主要是介绍【hiho一下 第四十一周】骨牌覆盖问题·一,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原题地址:http://hihocoder.com/contest/hiho41/problem/1
骨牌,一种古老的玩具。今天我们要研究的是骨牌的覆盖问题:
我们有一个2xN的长条形棋盘,然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘,一共有多少种不同的覆盖方法呢?
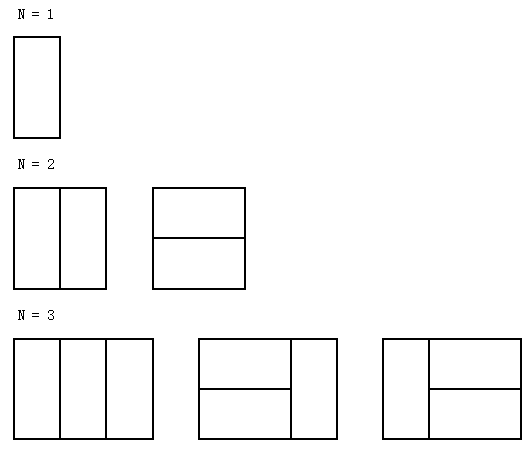
举个例子,对于长度为1到3的棋盘,我们有下面几种覆盖方式:
第1行:1个整数N。表示棋盘长度。1≤N≤100, 000, 000
第1行:1个整数,表示覆盖方案数 MOD 19999997
62247088
17748018
对于这个题目,采用动态规划的方法来解决。我们只需要考虑当前步骤如何来摆放骨牌,后续的即可转化为子问题。
从上面图中,我们可以清楚的看出,在每一步摆放骨牌的时候,要么是竖着放1块骨牌,要么是横着放2块骨牌,而且显然竖着放1块和横着放两块是不同的两种方案,其构成的是不同的解决方案。如果我们用f(n)来表示长度为n时的解决方案数,那么我们可以将其化为两个子问题:
- 如果我们第一步放置一个竖着的骨牌,则其后面的n-1个棋盘有f(n-1)种摆法;
- 如果我们第一步放置两个横着的骨牌,则其后面的n-2个气派有f(n-2)种摆法。
这就是斐波那契数列了。
#include <stdio.h>int count(int n) {if (n < 1)return 0;else if (n <= 2)return n;int arg1 = 1, arg2 = 2, i;for (i = 3; i < n; ++i)if (i & 1) {arg1 += arg2;arg1 %= 19999997;}else {arg2 += arg1;arg2 %= 19999997;}return (arg1 + arg2) % 19999997;
}int main() {int n;while (scanf("%d", &n) != EOF)printf("%d\n", count(n));return 0;
}个人学习记录,大神勿喷 // sfg1991@163.com // 2015-04-20
这篇关于【hiho一下 第四十一周】骨牌覆盖问题·一的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






