puzzle（0411）《骨牌》覆盖、染色

目录

一，2格骨牌覆盖问题

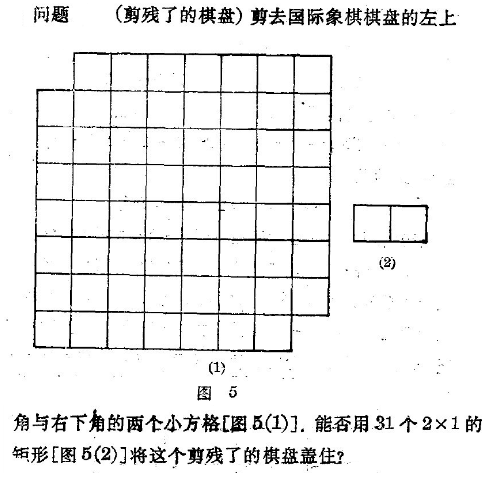
1，剪残了的棋盘

2，算法谜题 12 平铺多米诺问题

二，3格骨牌覆盖问题

1，算法谜题 78 直三格板平铺

2，L骨牌覆盖问题

三，4-5格骨牌覆盖问题

1，算法谜题 38 四格骨牌平铺问题

2，智力游戏 打包1

3，智力游戏 打包2

4，智力游戏 打包3

5，日历拼图

6，立方体拼图

四，染色技巧

1，染色的本质

2，4格覆盖问题

3，常见染色方式

---

一，2格骨牌覆盖问题

1，剪残了的棋盘

不知道为什么，想起了KMP。。。

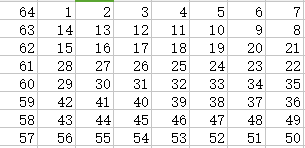
言归正传，既然待匹配项为1*2的长方形，那么可以把棋盘哈希到整数，分析奇偶性。

这个题目很简单，因为有个很简单的哈希函数：f=x+y，即国际象棋的棋盘。

所以答案是不能。

如果，减掉一个白格子和一个黑格子，那又能不能覆盖呢？

答案是能。

把64个格子弄成1个环

减掉2个格子之后，环变成2个线段。

因为2个格子一白一黑，所以2个线段的长度都是偶数。

所以2个线段都可以用1*2覆盖。

2，算法谜题 12 平铺多米诺问题

        能否用单位长度 2*1 的多米诺牌将 8*8 的方格阵铺满? 里面不包含由两张 2*1 多米诺并行排列而成的 2*2 的正方形。
        答案: 所要求的平铺方法不可能实现。

        本题可用反证法证明。假设这样的平铺方法可以实现, 由于方格板是对称的, 我们假设它的左上角是被如图 4.6 所示的一块横置的多米诺牌 1 所覆盖, 那么, 第二行第一列的方格必然是被一块坚直排放的多米诺牌覆盖, 因此, 同行第二列会是一块横放的多米诺牌。按照这个思路推演下去, 我们会得到图 4.6 所示的平铺图。 在多米诺牌 13 之下放一块横置的多米诺牌, 变成了唯一的选择, 这与没有两张多米诺牌并行排列形成 2*2 的正方形的条件矛盾。

二，3格骨牌覆盖问题

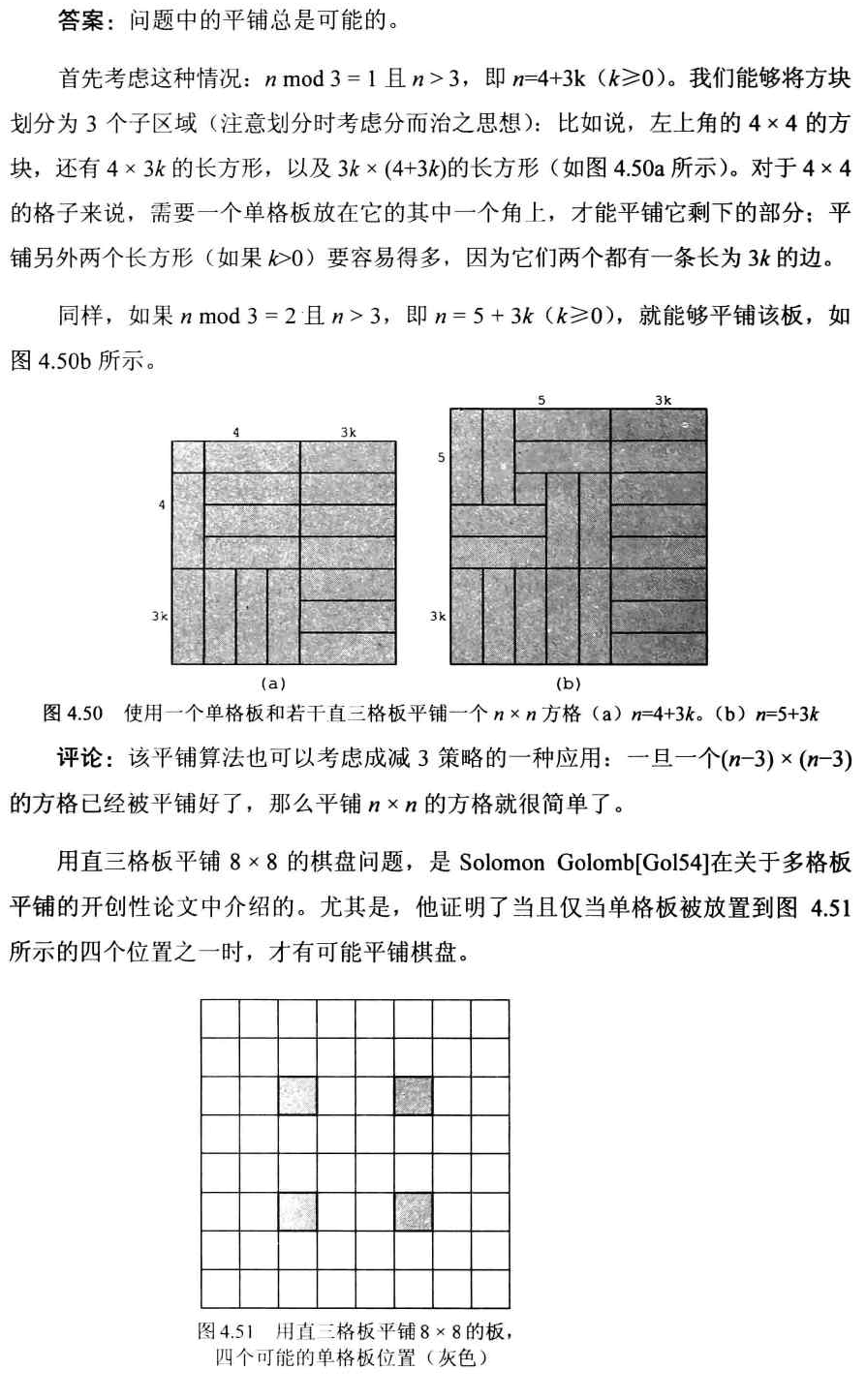
1，算法谜题 78 直三格板平铺

 一个直三格板是一个 3 *1 的瓦片平铺。很显然, 只要 n 能够被 3 整除, 任何人都能够通过直三格板平铺成一个 n *n 的正方形。那么, 对于一个大于 3 而又不能被 3 整除的 n 来说, 是否能够利用直三格板和一个叫做单格板的 1 * 1 瓦片平铺, 来构成一 个 n *n 的正方形?

2，L骨牌覆盖问题

边长为2^k的正方形，少了一个格子，如何用L型骨牌覆盖？

可以采用分治法：

三，4-5格骨牌覆盖问题

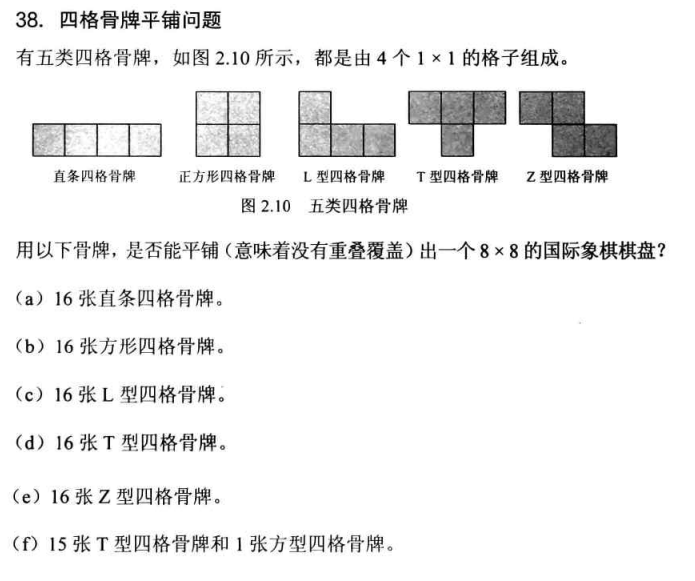
1，算法谜题 38 四格骨牌平铺问题

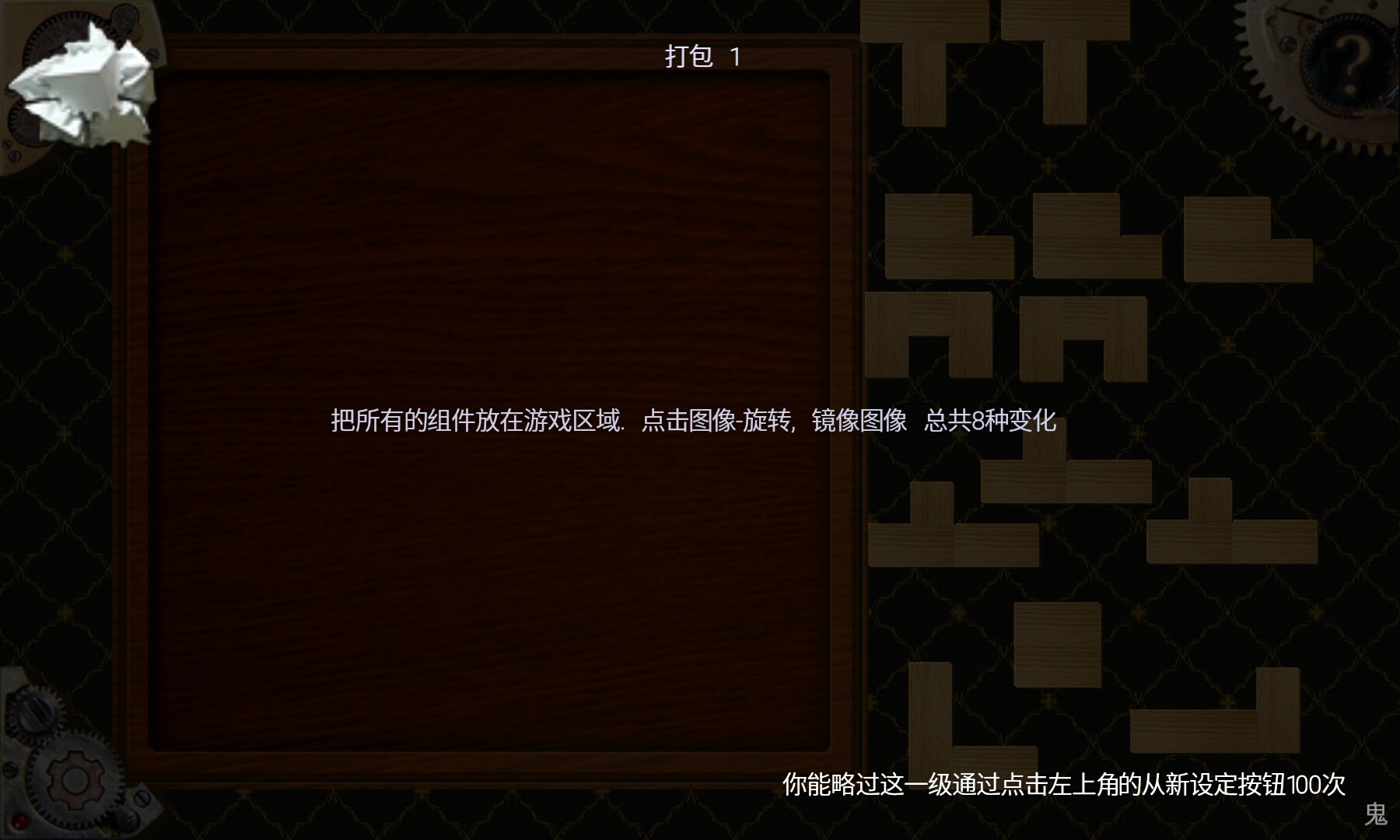
2，智力游戏 打包1

智力游戏

 

这一关，就是要把所有的木块不重叠的放进正方形。

因为正方形的边长为8，所以有64个格子。

对于木块，除了正方形之外，另外12个都有5个格子，所以一共也是64个格子。

所以最后应该是恰好铺满才对。

答案：

3，智力游戏 打包2

 

规则同上，但是木块不一样，这一关，木块是11个一样的木块，所以最后会有9个空格子。

答案：

4，智力游戏 打包3

5，日历拼图

https://blog.csdn.net/nameofcsdn/article/details/123765415

6，立方体拼图

根据X算法算出来的答案可以拼成立方体：

 

 

 

 

四，染色技巧

1，染色的本质

染色的本质是把整个平面划分成若干个集合，根据每个部件在各个集合中的数量满足的条件，推出整体满足的数量规律。

当然，一般划分都是很有规律的。

2，4格覆盖问题

问题：用1个2*2和15个1*4可以覆盖8*8吗？

答案是不能，有2类染色法。

第一类，使得2*2为奇，1*4为偶

第二类，使得2*2为偶，1*4位奇

这2个图都强有力的说明了题目的答案是不能。

3，常见染色方式

棋盘染色法的分类与应用