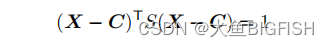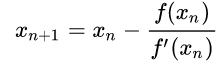迭代法专题
559. N 叉树的最大深度(迭代法)
目录 一:题目: 二:代码: 三:结果: 一:题目: 给定一个 N 叉树,找到其最大深度。 最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。 N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。 二:代码: /*// Definition for a Node.class Node {public:int val;vector<N
5、梯度下降法,牛顿法,高斯-牛顿迭代法
1、梯度下降 2、牛顿法 3、高斯-牛顿迭代法 4、代码部分 1.梯度下降法代码 批量梯度下降法c++代码: /*需要参数为theta:theta0,theta1目标函数:y=theta0*x0+theta1*x1;*/#include <iostream>using namespace std;int main()
589. N 叉树的前序遍历(迭代法)
目录 一:题目: 二:代码: 三:结果: 一:题目: 给定一个 n 叉树的根节点 root ,返回 其节点值的 前序遍历 。 n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。 二:代码: /*// Definition for a Node.class Node {public:int val;vector<Node*
PCL 拟合二维椭圆(迭代法)
文章目录 一、简介二、实现代码三、实现效果参考资料 一、简介 一般情况,我们会用椭圆拟合二维点,用椭球拟合三维点。在n维中,这些对象被称为超椭球体,由二次方程隐式定义 超椭球的中心是n×1向量C,n×n矩阵S是正定的,n×1向量X是超椭球上的任意点。矩阵S可以用特征分解,S = R D R T RDR^T RD
Newton迭代法例题
课本25页例2——7 #include<iostream>#include<math.h>using namespace std;int main(){cout<<"请输入初始值X:"<<endl;double x0,x1,F0,F1,F2,F3;cin>>x0;F0=x0*exp(x0)-1;F1=exp(x0)*(1+x0);int i;for( i=0;i<50;i++){if
matlab实现牛顿迭代法求解非线性方程组
已知非线性方程组如下 3*x1-cos(x2*x3)-1/2=0 x1^2-81*(x2+0.1)^2+sin(x3)+1.06=0 exp(-x1*x2)+20*x3+(10*pi-3)/3=0 求解要求精度达到0.00001 ---------------------------------------------------------分--割--线------------
强化学习实践二:迭代法评估4*4方格世界下的随机策略
本篇用代码演示《强化学习》第三讲中的示例——方格世界,即用动态规划算法通过迭代计算来评估4*4方格世界中的一个随机策略。具体问题是这样: 已知(如上图): 状态空间 S:为非终止状态;,终止状态,图中灰色方格所示两个位置;行为空间 A:{n, e, s, w} 对于任何非终止状态可以有向北、东、南、西移动四个行为;转移概率 P:任何试图离开方格世界的动作其位置将不会发生改变,其余条件下将1
C++实现牛顿迭代法求解f(x)=0
#include <iostream> #include <cmath> using namespace std; #define f(x) x*x - 8 #define df(x) 2*x double EPS = 1e-6; double Newton(double xFirst) { double xSecond; int iteCount = 0;//迭代次数
HDU2899 Strange fuction(牛顿迭代法)
最近刚学完数值分析上的方程求根——牛顿法,所以做几题练习一下。 Problem Description Now, here is a fuction: F(x) = 6 * x^7+8*x^6+7*x^3+5*x^2-y*x (0 <= x <=100) Can you find the minimum value when x is between 0 and 100.
Leetcode 144:二叉树的前序遍历(迭代法)
迭代法:就是不使用递归,利用while循环,重复执行循环体内的代码求解。 思路:利用栈存储节点,然后先让右节点入栈,再让左节点入栈。出栈时才是左、右的顺序。 //前序遍历//迭代法:重复执行一段代码来求解//利用栈,先将根节点的右孩子放进栈,再将左孩子放进栈public static List<Integer> preorderTraversal(TreeNode root){List<Int
迭代法和递归法的区别
迭代法和递归法都是求解问题的方法,它们的主要区别在于解决问题的思路和代码的实现方式。 迭代法是通过循环来重复执行相同的操作,每次迭代都将问题的规模减小一点,直到达到问题的终止条件为止。迭代法通常使用循环结构,代码相对简单直观,容易理解和实现。下面是一个用迭代法求阶乘的示例: int factorial(int n) {int result = 1;for (int i = 1; i <= n;
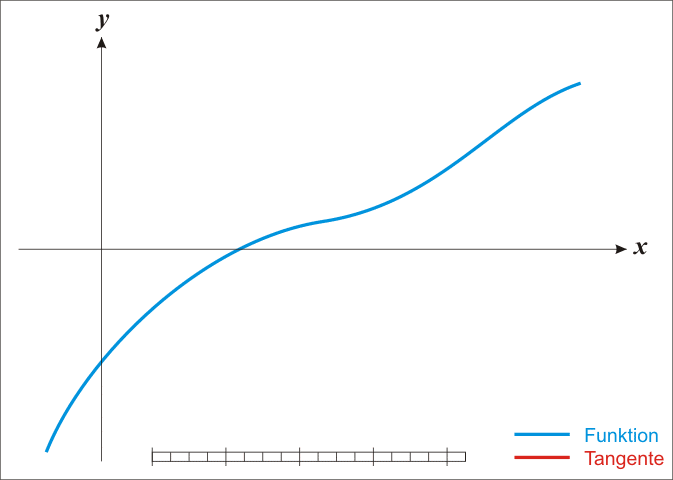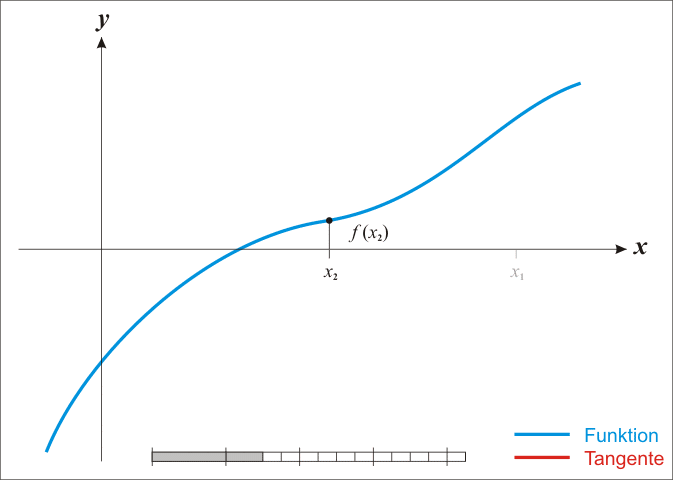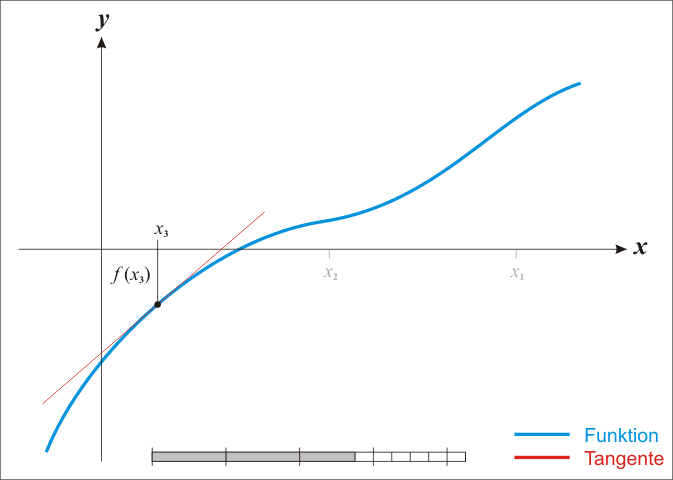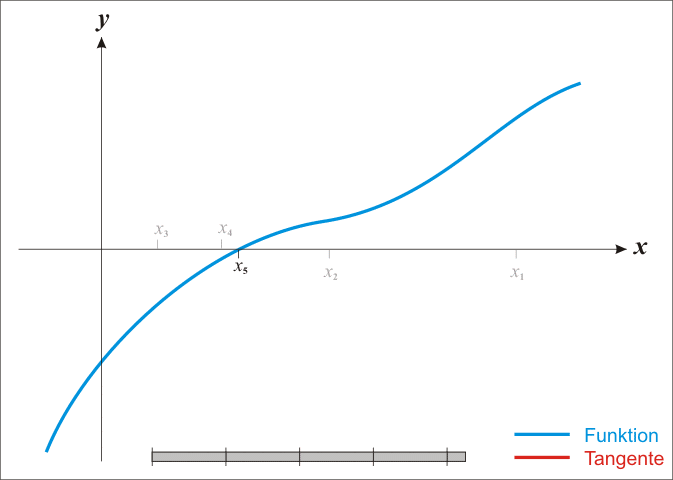
牛顿迭代法的可视化详解
来源:DeepHub IMBA本文约1800字,建议阅读10分钟本文利用可视化方法,为你直观地解析牛顿迭代法。 牛顿迭代法(Newton's method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。 以 Isaac Newton 和 Joseph Raphson 命名的 Newton-R
基于选权迭代法的Savitzky_Golay平滑算法
中心思想 在基于最小二乘原理对多项式进行拟合时,引入观测值的权值,有明显偏差的信号给予较小的权值,不含明显偏差的信号给予较大的权值,此时最小而成的优化函数有min(VTV) 变为min(VTPV),其中P是根据某次平差的改正数V基于的权值,在下面的代码中P=1/|V|,迭代求解,知道两次结果的差小于给定的阈值 import numpy as npclass Robust(object):def
C语言题目:迭代法求平方根
题目描述 用迭代法求 平方根 公式:求a的平方根的迭代公式为: X[n+1]=(X[n]+a/X[n])/2 要求前后两次求出的差的绝对值少于0.00001。 输出保留3位小数 输入格式 X 输出格式 X的平方根 样例输入 4 样例输出 2.000 代码解释 包含标准输入输出库和数学库: #include <stdio.h> 和 #include <math.h>
代码随想录算法训练营DAY14|C++二叉树Part.1|二叉树的递归遍历、二叉树的迭代遍历、二叉树的统一迭代法
文章目录 二叉树的递归遍历思路CPP代码 二叉树的迭代遍历思路前序遍历后序遍历后序遍历 二叉树的统一迭代法 二叉树的递归遍历 144.二叉树的前序遍历、145.二叉树的后序遍历、94.二叉树的中序遍历 文章讲解:二叉树的递归遍历 视频讲解:每次写递归都要靠直觉? 这次带你学透二叉树的递归遍历! 状态:搞清楚本题就一定要先搞清楚递归是什么,曾经可能需要靠栈来想想递归的工作流程,
【算法】归并排序(迭代法)
简介 归并排序有两种实现方法: 递归法(Top-down implementation)迭代法(Bottom-up implementation) 关于归并排序的介绍请看之前的 归并排序(递归法)。 算法步骤(迭代) 设待排列序列有 n 个序列。子序列宽度为 width = 1。 将宽度为 width 的子序列每对相邻两个子序列进行归并操作,形成新序列,排序后每个序列包含 width
力扣面试150 x 的平方根 二分 换底法 牛顿迭代法 一题多解
Problem: 69. x 的平方根 思路 👨🏫 参考题解 💖 袖珍计算器算法 class Solution {public int mySqrt(int x){if (x == 0)return 0;// Math.exp(3):e的三次方int ans = (int) Math.exp(0.5 * Math.log(x));return (long) (a
代码随想录笔记|C++数据结构与算法学习笔记-二叉树(一)|二叉树的递归遍历、二叉树的迭代遍历、二叉树的统一迭代法
全文基于代码随想录及相关讲解视频。 文字链接:《代码随想录》 文章目录 二叉树的递归遍历二叉树的前序遍历C++代码如下 二叉树的中序遍历二叉树的后序遍历 二叉树的迭代遍历前序遍历前序遍历C++代码 右序遍历右序遍历C++代码 中序遍历为什么中序遍历不同中序遍历迭代法的过程中序遍历C++代码 二叉树的统一迭代法中序遍历前序遍历后序遍历 二叉树的递归三部曲:(非常重要,每一题几乎
算法#01--素数和牛顿迭代法求平方根
素数 1.概念 质数(prime number)又称素数,有无限个。除了1和它本身以外不再有其他的除数整除。根据算术基本定理,每一个比1大的整数,要么本身是一个质数,要么可以写成一系列质数的乘积,最小的质数是2。 2.论点 在一般领域,对正整数n,如果用2到根号n之间的所有整数去除,均无法整除,则n为质数。 3.证明 如果n不能被2到根号n之间的任一整数整除,且不是质数,那么n可以表示
【软件设计师】常见的算法设计方法——迭代法
🐓 迭代法 什么是迭代法 迭代法,作为一种重要的算法思想,在计算机科学、数学以及其他多个领域中都有着广泛的应用。那么,什么是迭代法呢? 简单来说,迭代法是一种通过不断重复某个过程来逐步逼近问题解的方法。 它从一个初始的近似解出发,按照某种规则或公式不断地进行迭代计算,直到满足某个终止条件,从而得到问题的近似解或精确解。 想象一下,你在一个漆黑的房间中,试图找到一扇打开的门。
牛顿迭代法(Newton's Method)
高次方程没有通解,可以依靠牛顿迭代法来求解。 五次及以上多项式方程没有根式解(就是没有像二次方程那样的万能公式),这个是被伽罗瓦用群论做出的最著名的结论。 但是,没有王屠夫难道非得吃带毛猪?工作生活中还是有诸多求解高次方程的真实需求(比如行星的轨道计算,往往就是涉及到很复杂的高次方程),这日子可怎么过下去啊? 没有根式解不意味着方程解不出来,数学家也提供了很多方法,牛顿迭代法就是其中一种。http
C语言OJ项目参考(2405)牛顿迭代法求根
2405: 牛顿迭代法求根 Description 用牛顿迭代法求根。方程为 ax3+bx2+cx+d=0 ax^3+bx^2+cx+d=0。系数a,b,c,d的值一次为1,2,3,4,由主函数输入。求x在1附近的一个实根。求出根后由主函数输出。结果保留两位小数。 Input 系数a,b,c,d的值 Output x在1附近的一个实根 Sample Input 1 2 3 4 S
子空间迭代法 matlab,matlab子空间迭代法求结构频率和振型
子空间迭代法求图示结构前2阶频率和振型 syms m k w; K=[k -k 0 0 0 -k 2*k -k 0 0 0 -k 2*k -k 0 0 0 -k 2*k –k 0 0 0 -k 2*k]; %刚度矩阵 M=[m 0 0 0 0;0 m 0 0 0;0 0 m 0 0;0 0 0 m 0;0 0 0 0 m] ; %质量矩阵 fi1=m/k*[ 15, 5; 14, 4;12, 3