本文主要是介绍牛顿迭代法(Newton's Method),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
高次方程没有通解,可以依靠牛顿迭代法来求解。
五次及以上多项式方程没有根式解(就是没有像二次方程那样的万能公式),这个是被伽罗瓦用群论做出的最著名的结论。
但是,没有王屠夫难道非得吃带毛猪?工作生活中还是有诸多求解高次方程的真实需求(比如行星的轨道计算,往往就是涉及到很复杂的高次方程),这日子可怎么过下去啊?
没有根式解不意味着方程解不出来,数学家也提供了很多方法,牛顿迭代法就是其中一种。
https://www.matongxue.com/madocs/205.html
牛顿迭代法在acm中的应用:
1.求解方程的根
枚举初始迭代点求f'(x) = 0 的根
HDU2899
2.开根号
牛顿迭代法相比于二分法,迭代次数更少。
而且在雷神之锤3的源码中还有一个更强大的求1/sqrt(a)的方法,比c++ 标准库快好几倍
其源码如下所示:
float Q_rsqrt( float number )
{long i;float x2, y;const float threehalfs = 1.5F;x2 = number * 0.5F;y = number;i = * ( long * ) &y; // evil floating point bit level hackingi = 0x5f3759df - ( i >> 1 ); // what the fuck?y = * ( float * ) &i;y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed#ifndef Q3_VM#ifdef __linux__assert( !isnan(y) ); // bk010122 - FPE?#endif#endifreturn y;
}关于注释为"what the fuck?"的一行,这里有一篇论文:http://www.matrix67.com/data/InvSqrt.pdf
之所以会出现这种奇怪的注释,要么是此段程序的作者(可能是马克尔)根本不知道该如何解释清楚,或者是维护这段程序的程序员完全看不懂这句话,所以有点儿抓毛。而实际上,它的作用(再加上y
= y * ( threehalfs - ( x2 * y * y ) )这句牛顿迭代)就是求平方根。
求解1/sqrt(a) = x (脑补对任意根号下的解)
1/(x^2) - a = 0
令f(x) = 1/(x^2) - a
f'(x) = -2/(x^3)
xn+1 = xn - f(xn) / f'(xn) = x*(1.5 -0.5a*x^2)
参考雷声之锤(一款游戏)源码,我们得到一个速度更优的求sqrt(a)的方法
double Sqrt(float x){double xhalf = 0.5*(double)x;int i = *(int*)&x; // get bits for floating VALUEi = 0x5f375a86- (i>>1); // gives initial guess y0x = *(float*)&i; // convert bits BACK to floatx = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracyx = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracyx = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracyreturn 1.0/(double)x;
} https://blog.csdn.net/wubaizhe/article/details/75574798
https://www.cnblogs.com/widsom/p/8857108.html
https://www.2cto.com/kf/201206/137256.html
迭代法求平方根的通式: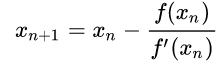
最后根据值得精度,跳出迭代得到根
这篇关于牛顿迭代法(Newton's Method)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






![The remote endpoint was in state [TEXT_FULL_WRITING] which is an invalid state for called method 已解决](/front/images/it_default2.jpg)


