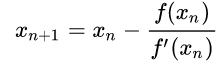newton专题
Discusss about the newton's method(on youtube)
Discuss about the newton's video on Youtube: https://www.youtube.com/watch?v=-DpZOZTsdvg Luis Reguera 11 months ago so...if Newton's method doesn't work...which is the alternativ
Newton迭代法例题
课本25页例2——7 #include<iostream>#include<math.h>using namespace std;int main(){cout<<"请输入初始值X:"<<endl;double x0,x1,F0,F1,F2,F3;cin>>x0;F0=x0*exp(x0)-1;F1=exp(x0)*(1+x0);int i;for( i=0;i<50;i++){if
数值积分之Newton_Cotes闭合积分公式
//Newton_Cotes闭合积分公式 #include <iostream> #include <math.h> using namespace std; class trapezoidal { private: int n, k; double a, b, f, h, integral, sum; public: double func(double v) { f = 24
Newton's Telecom Dictionary: Covering Telecommunications, Networking, Information Technology, Comput
版权声明:原创作品,允许转载,转载时请务必以超链接形式标明文章原始出版、作者信息和本声明。否则将追究法律责任。 http://blog.csdn.net/topmvp - topmvp Newton's Telecom Dictionary helps technology and business professionals stay on top of the ever-changing
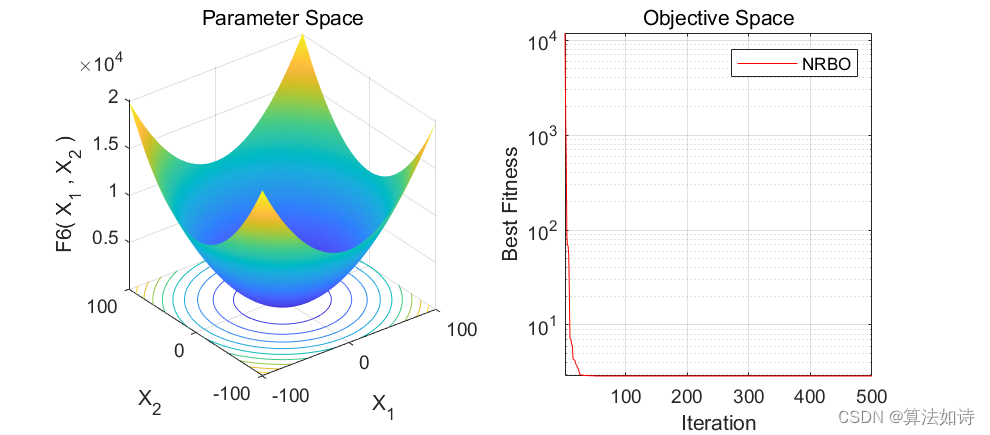
智能优化算法 | Matlab实现牛顿-拉夫逊优化算法Newton-Raphson-based optimize(内含完整源码)
文章目录 效果一览文章概述源码设计参考资料 效果一览 文章概述 智能优化算法 | Matlab实现牛顿-拉夫逊优化算法Newton-Raphson-based optimize(内含完整源码) 源码设计 % --------------------------------------------------------------------------
数值分析复习:Newton插值
文章目录 牛顿(Newton)插值引入背景插值条件基函数插值多项式差商差商的基本性质差商估计差商的Leibniz公式 余项估计 本篇文章适合个人复习翻阅,不建议新手入门使用 牛顿(Newton)插值 引入背景 Lagrange插值每引入一个新节点,就要重新计算所有基函数,计算代价大 插值条件 n+1个插值节点 x 0 , x 1 , … , x n x_0,x_
牛顿迭代法(Newton's Method)
高次方程没有通解,可以依靠牛顿迭代法来求解。 五次及以上多项式方程没有根式解(就是没有像二次方程那样的万能公式),这个是被伽罗瓦用群论做出的最著名的结论。 但是,没有王屠夫难道非得吃带毛猪?工作生活中还是有诸多求解高次方程的真实需求(比如行星的轨道计算,往往就是涉及到很复杂的高次方程),这日子可怎么过下去啊? 没有根式解不意味着方程解不出来,数学家也提供了很多方法,牛顿迭代法就是其中一种。http
matlab scanf函数,牛顿迭代法(牛顿-拉弗森方法(Newton-Raphson method))
起源[编辑] 牛顿法最初由艾萨克·牛顿在Method of Fluxions,1671年完成,在牛顿死后的1736年公开发表)。约瑟夫·拉弗森也曾于1690年在 方法说明[编辑] 蓝线表示方程 f而红线表示切线. 可以看出 x n+1比 x n更靠近 f所要求的根 x. 首先,选择一个接近函数 零点的 ,计算相应的 和切线斜率 (这里 表示函数 的导数)。然后我们计算穿过点 并且斜率为 的
Logistic Regression and Newton's Method
close all,clear,clcx = load('ex4x.dat');y = load('ex4y.dat');% find returns the indices of the% rows meeting the specified conditionpos = find(y == 1); %得到被录取学生的下标序列neg = find(y == 0); %得到没有录取学生
非线性最小二乘法之Gauss Newton、L-M、Dog-Leg
非线性最小二乘法之Gauss Newton、L-M、Dog-Leg 最快下降法 假设 hTF′(x)<0 h^TF'(x) < 0,则h是 F(x) F(x)下降方向,即对于任意足够小的 α>0 \alpha > 0,都满足 F(x+αh)<F(x) F(x+ \alpha h) < F(x)。 现在讨论 F(x) F(x)沿着h方向下降快慢: limα→0F(x)−F(x+αh)
机器学习提高班---优化(梯度下降,最速下降,Newton下降算法)(week 3)
机器学习与凸优化讨论班于11月24日晚上在致远楼教室举办。在本次讨论班上,王文川同学为大家详细介绍了无约束优化问题的几种主要算法。 首先,王文川同学为大家介绍了无约束优化问题的定义,并举了简单的例子,说明迭代算法解决该类问题的必要性,还讲解了强凸性假设和条件数的概念,为后面算法的收敛性做知识铺垫。 然后,王文川同学介绍了通用的下降算法框架,包括初始点、搜索方向和步长三个要素。他又详细讲解了两种确定
【数值计算方法(黄明游)】函数插值与曲线拟合(二):Newton插值【理论到程序】
文章目录 一、近似表达方式1. 插值(Interpolation)2. 拟合(Fitting)3. 投影(Projection) 二、Lagrange插值1. 拉格朗日插值方法2. Lagrange插值公式a. 线性插值(n=1)b. 抛物插值(n=2) 三、Newton插值1. 天书2. 人话3. 例题4. python实现5. C语言实现 一、近似表达方式 插值、
数值积分编程基础-牛顿科特斯(Newton-Cotes)(python)
第三十九篇 数值积分-牛顿柯特斯 当以解析法去求代数积分时不便利或者根本求不出来时,就使用数值积分或“求积”的方式。数值积分方法可以应用在数学函数,或者针对工程实验中能够测量的离散数据。首先考虑一元函数的数值积分方法,即: 多个变量函数的面积和体积积分将在后面讨论。 本篇将介绍几种数值积分公式(也称为“法则”)。这些方法通常不依赖于被积分的函数类型,但一些“自定义”方法也会被讨论。 少数情况下
Optimization之GD,Newton Method
gradient descentNewtons MethodMomentumAdagradRMSPropAdam 转载请注明出处: http://blog.csdn.net/c602273091/article/details/79111771 机器学习或者是深度学习中涉及了不少优化理论,那么问题来了,在机器学习中,它优化的目标是什么?它是如何进行优化的?为什么进行这种优化?这种
站在巨人的肩膀上___An Animated Google Doodle for Newton’s Apple Tree
声名:请用科学的态度或一笑置之阅读这篇文章。流畅的文笔,只能出于自由的心灵。所有的迷信都是需要破除的,不管他来自哪里,属何方神圣! 牛顿老师 在科学圈里曾经很有权势,被女王封了爵位成了贵族,人称牛爵爷,官至皇家造币局局长兼皇家学会会长。如果阿尔伯特没有辞了以色列总统的话和他有一拼。 说他有权势并不仅是官大,主要还是贡献大。如果17世纪就有诺贝尔奖的话,牛顿老师至少
【转】Gauss-Newton优化方法 含代码
Gauss-Newton算法是解决非线性最优问题的常见算法之一,最近研读开源项目代码,又碰到了,索性深入看下。本次讲解内容如下: 基本数学名词识记牛顿法推导、算法步骤、计算实例高斯牛顿法推导(如何从牛顿法派生)、算法步骤、编程实例高斯牛顿法优劣总结 一、基本概念定义 1.非线性方程定义及最优化方法简述 指因变量与自变量之间的关系不是线性的关系,比如平方关系、对数关系
Newton插值法 | matlab实现
function y_p = Newton(x, y, x_p)% x为插值节点的横坐标% y为插值节点的纵坐标% x_p 为需计算的插值函数值的横坐标% y_p 为插值函数值i = length(x) - 1;iter = 1;num = length(x_p);y_i = y(1);y_p = [];%for n = 1: numdif_quo = []; % 存放差商whi
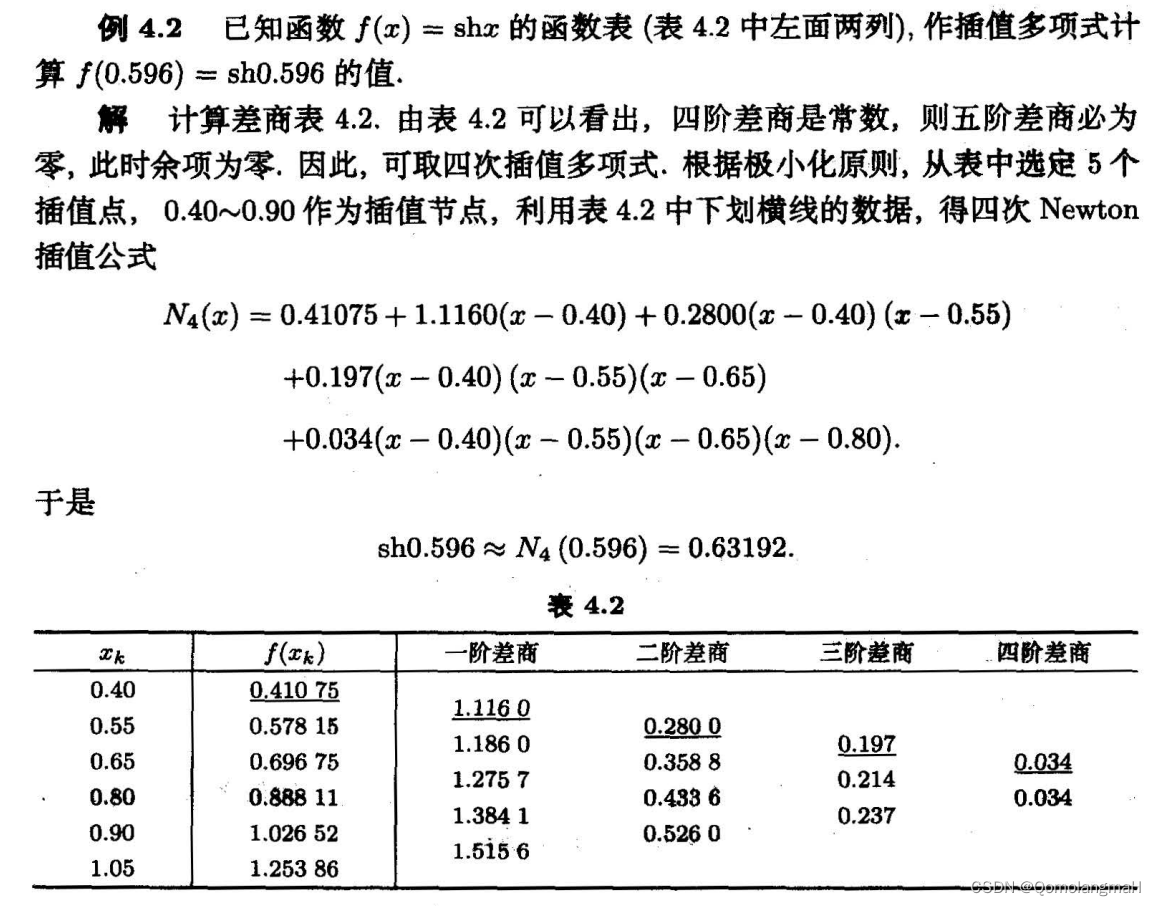
Newton插值法 | 差商 + Newton插值公式 + 插值余项
Newton插值法 Aitken逐次插值法虽然具有承袭性的特点,但其插值公式是递推型的,不便于进行理论分析。为此,可以把n次插值多项式改写成升幂的形式: N n ( x ) = c 0 + c 1 ( x − x 0 ) + c 2 ( x − x ) ( x − x 1 ) + ⋯ + c n ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n − 1 ) (10) N_