机器学习提高班---优化(梯度下降，最速下降，Newton下降算法)（week 3）

机器学习与凸优化讨论班于11月24日晚上在致远楼教室举办。在本次讨论班上，王文川同学为大家详细介绍了无约束优化问题的几种主要算法。
首先，王文川同学为大家介绍了无约束优化问题的定义，并举了简单的例子，说明迭代算法解决该类问题的必要性，还讲解了强凸性假设和条件数的概念，为后面算法的收敛性做知识铺垫。
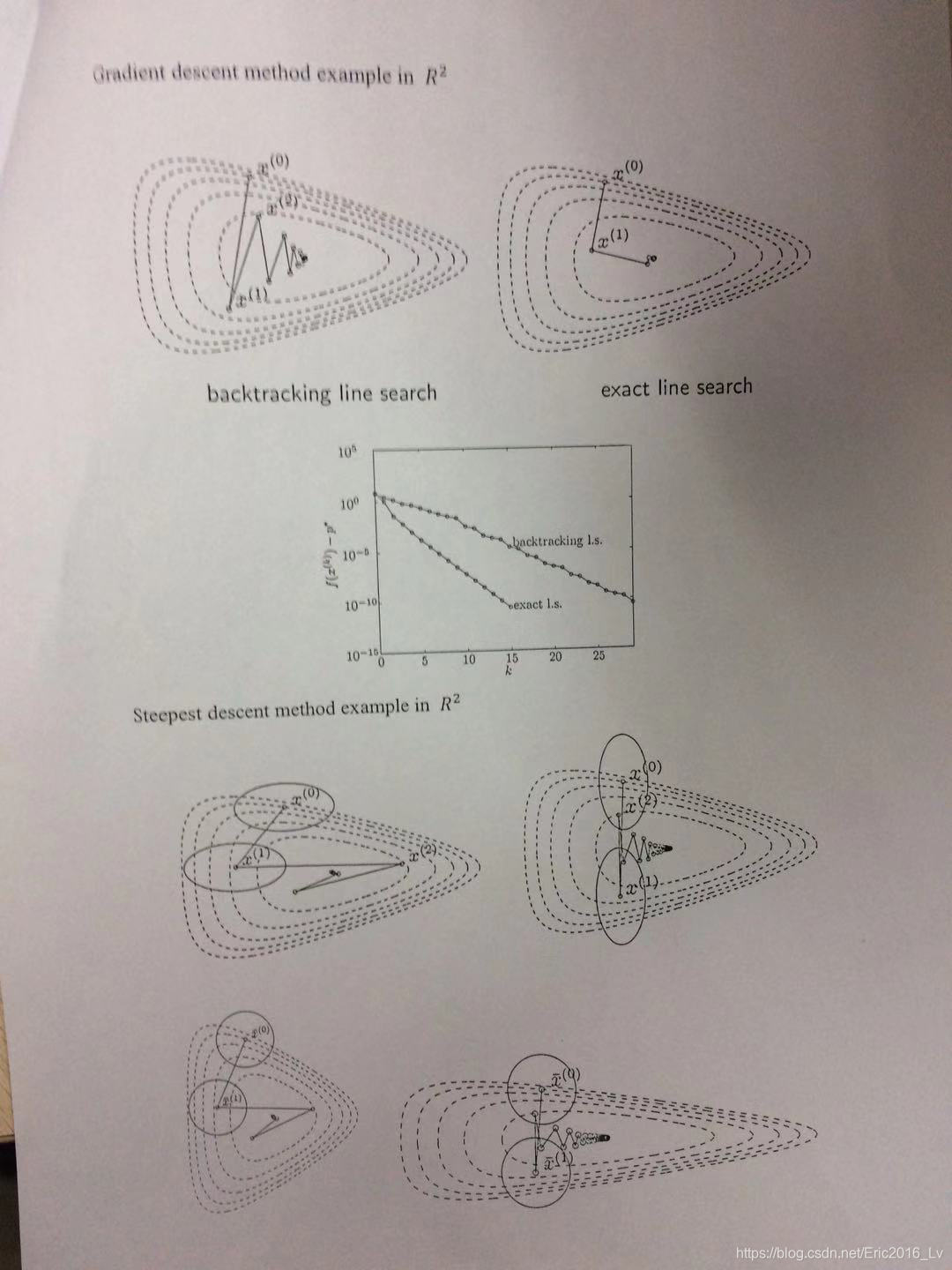
然后，王文川同学介绍了通用的下降算法框架，包括初始点、搜索方向和步长三个要素。他又详细讲解了两种确定步长的方式，精确直线搜索与回溯直线搜索，并解释了两种方法的合理性。

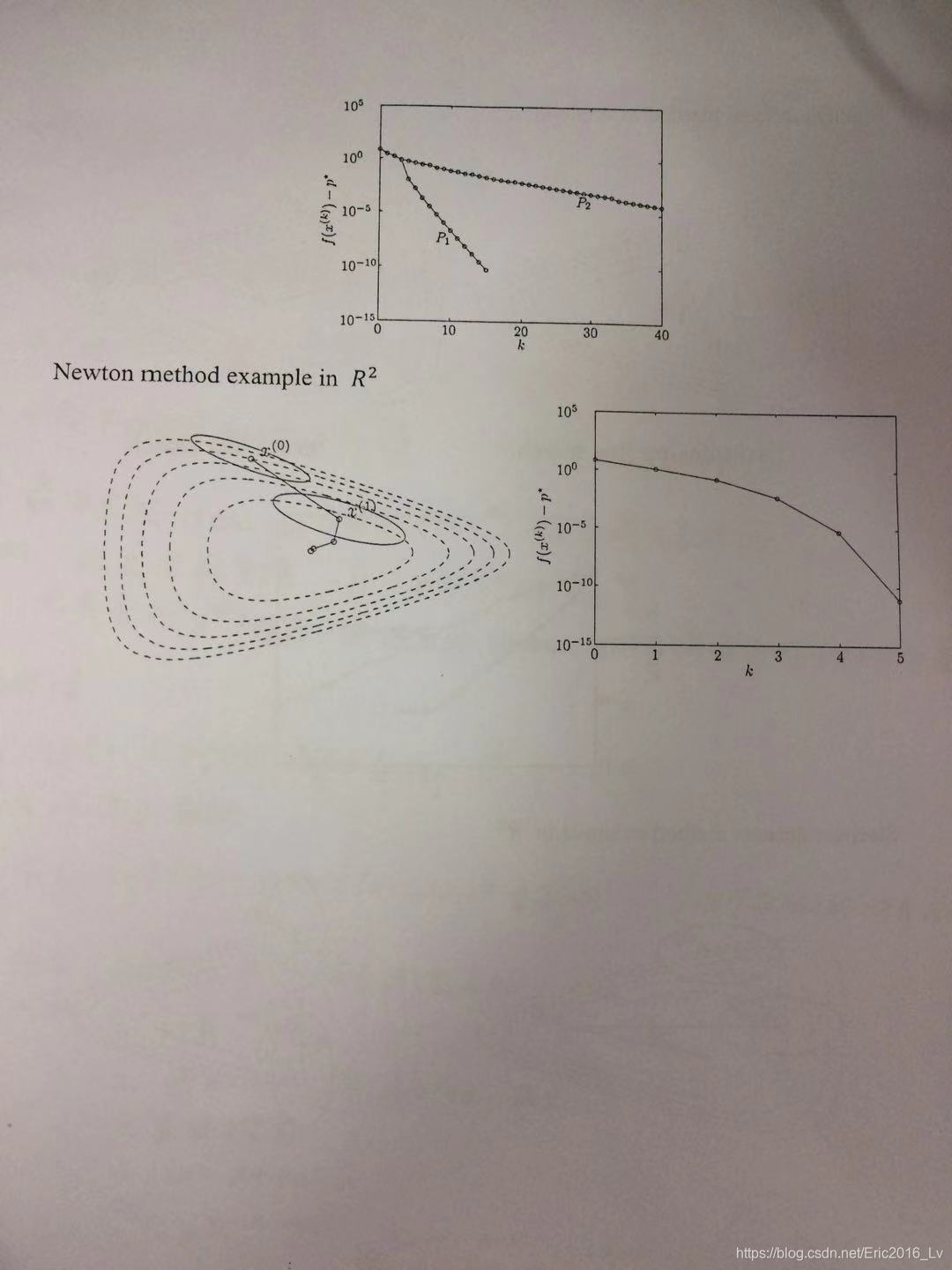
最后，王文川同学为大家讲解了搜索方向确定的方法，包括梯度下降、最速下降和牛顿法。对于每种算法，他都用直观的例子解释了收敛速度不同的原因。另外，他还用公式推导阐述了这三种下降算法之间的内在联系，使不同算法的优劣性更易理解。
无约束优化是优化方法的基本组成部分，也是优化问题中较常用的算法。实践中的大多数问题是具有约束的优化问题，但是在处理时可以将有约束问题部分转化为无约束问题。本次讨论班大家的互动积极，通过不断的提问和解释，大家对无约束优化算法及其优劣性能都有了较深的理解。

以下为上课的讲义：