本文主要是介绍非线性最小二乘法之Gauss Newton、L-M、Dog-Leg,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
非线性最小二乘法之Gauss Newton、L-M、Dog-Leg
最快下降法
假设 hTF′(x)<0 ,则h是 F(x) 下降方向,即对于任意足够小的 α>0 ,都满足 F(x+αh)<F(x) 。
现在讨论 F(x) 沿着h方向下降快慢:
其中 θ 为矢量h和 F′(x) 夹角,当 θ=π 时,下降最大。
即 hsd=−F′(x) ,是最快下降方向。
最小二乘问题
通常的最小二乘问题都可以表示为:
找到一个 x∗ 使得 x∗=argminxF(x) ,其中 x=[x1x2⋯xm] , f(x)=[f1(x)f2(x)⋯fn(x)] 。
假设对 f(x) 第 i 个分量
fi(xk+h)≈fi(xk)+∇fi(xk)Th , i=1,2⋯n
则 f(xk+h)≈f(xk)+J(xk)h ,其中Jacobin矩阵
通常记 fk=f(xk) , Jk=J(xk) .
所以 F(x) 的梯度:
GaussNewton
选择 h 使得
为使 F(xk+h) 取得极小值, L(h) 对h一阶导数 ∂L(h)∂h=JTkfk+JTkJkh ,令 L′(h)=0 ,则 (JTkJk)hgn=−JTkfk 。
当 JTkJk 非奇异的时候, hgn=−(JTkJk)−1JTkfk , xk+1=xk+hgn 。
由于GaussNewton求解过程中需要对 JTJ 求逆,所以当 JTJ 变成奇异的,GaussNewton方法失效。另外当 x0 离极小点较远时,GaussNewton算法可能会发散。
总结以上,GaussNewton法一般求解步骤:
- step1:根据 (JTkJk)hgn=−JTkfk ,求解迭代步长 hgn ;
- step2: xk+1=xk+hgn 进行新的迭代;
- step3:若 |F(xk+1)−F(xk)|<ϵ ,其中 ϵ 足够小,则认为 F(x) 以收敛,则退出迭代,否则重复step1;
通常GaussNewton法收敛较快,但是不稳定。而最快下降法稳定,但是收敛较慢。所以接下来我们介绍GaussNewton和最快下降法混合法。
LM阻尼最小二乘法
GaussNewton法是用 (JTkJk)h=−JTkfk 来确定 h ,现在假设在
(JTkJk+uI)h=−JTkfk
这样即使当 JTkJk 奇异,只要 u 取得充分大,总能使
因此 u 起着使步长
那么LM阻尼最小二乘法实际迭代过程中怎样调整 u ?
假设
则对 F(x+h) 二阶近似,
我们定义一个增益比 ρ=F(x)−F(x+hlm)L(0)−L(hlm)
在实际中,我们选择一阶近似、二阶近似并不是在所有定义域都满足的,而是在 [x−ϵ,x+ϵ] 作用域内满足这个近似条件。
当 ρ 较大时,表明 F(x+h) 的二阶近似 L(h) 比 F(x+h) 更加接近于 F(x) ,因此二阶近似比较好,所以可以减小 u ,采用更大的迭代步长,接近GaussNewton法来更快收敛;
而当
一种比较好的阻尼系数
初始值 A0=J(x0)TJ(x0) , u0=τ∗max{aii} , v0=2 ,算法对 τ 取值不敏感, τ 可以取 10−6 、 10−3 或者1都可以。
总结以上,LM阻尼最小二乘法求解步骤:
- step1:初始化 u0=τ∗max{aii} , v0=2 ;
- step2:求解梯度 gk=JTkfk ,如果 ∥gk∥≤ϵ1 ,则退出,否则继续;
- step3:根据 (JTkJk+ukI)hlm=−JTkfk ,求解迭代步长 hlm 。若 ∥hlm∥≤ϵ2(∥x∥+ϵ2) ,则退出迭代,否则继续;
- step4: xnew=xk+hlm ,计算增益比 ρ=F(xk)−F(xnew)L(0)−L(hlm) 。
如果 ρ>0 ,则 xk+1=xnew , uk+1=uk∗max{13,1−(2ρ−1)3} , vk+1=2 ;
否则 uk+1=uk∗vk , vk+1=2∗vk 。重复step2;
对于 ϵ1 、 ϵ2 可以选取任意小的值如 10−12 ,只是作为迭代的终止条件,其值得选取对最终的收敛结果影响不大。
Dog-Leg最小二乘法
另外一个GaussNewton和最快下降法混合方法是Dog-Leg法,代替阻尼项而是用trust region。
回到上面讲到最快下降法,下降方向 hsd=−F′(xk)=−JTkfk ,但是步进多长呢?或者沿着这个方向步进多长能使得 F(x) 取得最大程度的下降呢?
假设 f(x+αhsd)≈f(x)+αJ(x)hsd
为使得 F(x+αhsd) 最小,对 α 求导,
则如果GaussNewton法则 xk+1−xk=hgn ;如果最快下降法则 xk+1−xk=αhsd 。
继续trust region是什么呢?
trust region即为在 ∥h∥≤Δ 范围内, F(x+h)=F(x)+hTJTf+12hTJTJh 能够较好的近似,因此不管我们在选择GaussNewton还是最快下降法,必须满足 ∥∥hgn∥∥≤Δ 、 ∥αhsd∥≤Δ ,二阶近似才能较好成立。
然后继续,Dog-Leg迭代步长 hdl 和 hgn 、 αhsd 、 Δ 有什么关系?
hdl 和 hgn 、 αhsd 、 Δ 关系示意图:

和阻尼最小二乘法类似,实际中怎样更新trust region半径呢?
继续选择增益比 ρ=F(x)−F(x+hdl)L(0)−L(hdl)
总结以上,Dog-Leg最小二乘法求解步骤:
- step1:初始化 Δ0 。
- step2:求解梯度 gk=JTkfk ,如果 ∥gk∥≤ϵ1 ,则退出,否则继续。如果 ∥f(xk)∥≤ϵ3 ,则退出,否则继续。
- step3:如果trust region半径 Δk≤ϵ2(∥xk∥+ϵ2) ,则退出迭代;否则继续;
- step4:分别根据GaussNewton法和最快下降法计算 hgn 和 hsd ,然后计算最快下降法的迭代步长 α=∥g∥2∥J(x)g∥2 。
- step5:根据 hgn 、 hsd 和trust region半径 Δk ,来计算Dog-Leg步进值 hdl 。若 ∥hdl∥≤ϵ2(∥xk∥+ϵ2) ,则退出迭代;否则继续。
- step6: xnew=xk+hdl ,计算增益比 ρ=F(xk)−F(xnew)L(0)−L(hdl) 。
重复step2。
对于 ϵ1 、 ϵ2 、 ϵ3 可以选取任意小的值如 10−12 ,只是作为迭代的终止条件,其值得选取对最终的收敛结果影响不大。
举例:
拟合 f(x)=Asin(Bx)+Ccos(Dx) ,假设4个参数已知A=5、B=1、C=10、D=2,构造100个随机数作为x的采样值,然后计算 f(x) 再在上面加一个随机扰动量作为观测值。然后,利用输入与输出,来反推四个参数。
Gauss Newton代码:
double func(const VectorXd& input, const VectorXd& output, const VectorXd& params, double objIndex)
{// obj = A * sin(Bx) + C * cos(D*x) - Fdouble x1 = params(0);double x2 = params(1);double x3 = params(2);double x4 = params(3);double t = input(objIndex);double f = output(objIndex);return x1 * sin(x2 * t) + x3 * cos( x4 * t) - f;
}//return vector make up of func() element.
VectorXd objF(const VectorXd& input, const VectorXd& output, const VectorXd& params)
{VectorXd obj(input.rows());for(int i = 0; i < input.rows(); i++)obj(i) = func(input, output, params, i);return obj;
}//F = (f ^t * f)/2
double Func(const VectorXd& obj)
{return obj.squaredNorm()/2;
}double Deriv(const VectorXd& input, const VectorXd& output, int objIndex, const VectorXd& params,int paraIndex)
{VectorXd para1 = params;VectorXd para2 = params;para1(paraIndex) -= DERIV_STEP;para2(paraIndex) += DERIV_STEP;double obj1 = func(input, output, para1, objIndex);double obj2 = func(input, output, para2, objIndex);return (obj2 - obj1) / (2 * DERIV_STEP);
}MatrixXd Jacobin(const VectorXd& input, const VectorXd& output, const VectorXd& params)
{int rowNum = input.rows();int colNum = params.rows();MatrixXd Jac(rowNum, colNum);for (int i = 0; i < rowNum; i++){for (int j = 0; j < colNum; j++){Jac(i,j) = Deriv(input, output, i, params, j);}}return Jac;
}void gaussNewton(const VectorXd& input, const VectorXd& output, VectorXd& params)
{int errNum = input.rows(); //error numint paraNum = params.rows(); //parameter numVectorXd obj(errNum);double last_sum = 0;int iterCnt = 0;while (iterCnt < MAX_ITER){obj = objF(input, output, params);double sum = 0;sum = Func(obj);cout << "Iterator index: " << iterCnt << endl;cout << "parameter: " << endl << params << endl;cout << "error sum: " << endl << sum << endl << endl;if (fabs(sum - last_sum) <= 1e-12)break;last_sum = sum;MatrixXd Jac = Jacobin(input, output, params);VectorXd delta(paraNum);delta = (Jac.transpose() * Jac).inverse() * Jac.transpose() * obj;params -= delta;iterCnt++;}
}LM代码:
double maxMatrixDiagonale(const MatrixXd& Hessian)
{int max = 0;for(int i = 0; i < Hessian.rows(); i++){if(Hessian(i,i) > max)max = Hessian(i,i);}return max;
}//L(h) = F(x) + h^t*J^t*f + h^t*J^t*J*h/2
//deltaL = h^t * (u * h - g)/2
double linerDeltaL(const VectorXd& step, const VectorXd& gradient, const double u)
{double L = step.transpose() * (u * step - gradient);return L/2;
}void levenMar(const VectorXd& input, const VectorXd& output, VectorXd& params)
{int errNum = input.rows(); //error numint paraNum = params.rows(); //parameter num//initial parameter VectorXd obj = objF(input,output,params);MatrixXd Jac = Jacobin(input, output, params); //jacobinMatrixXd A = Jac.transpose() * Jac; //HessianVectorXd gradient = Jac.transpose() * obj; //gradient//initial parameter tao v epsilon1 epsilon2double tao = 1e-3;long long v = 2;double eps1 = 1e-12, eps2 = 1e-12;double u = tao * maxMatrixDiagonale(A);bool found = gradient.norm() <= eps1;if(found) return;double last_sum = 0;int iterCnt = 0;while (iterCnt < MAX_ITER){VectorXd obj = objF(input,output,params);MatrixXd Jac = Jacobin(input, output, params); //jacobinMatrixXd A = Jac.transpose() * Jac; //HessianVectorXd gradient = Jac.transpose() * obj; //gradientif( gradient.norm() <= eps1 ){cout << "stop g(x) = 0 for a local minimizer optimizer." << endl;break;}cout << "A: " << endl << A << endl; VectorXd step = (A + u * MatrixXd::Identity(paraNum, paraNum)).inverse() * gradient; //negtive Hlm.cout << "step: " << endl << step << endl;if( step.norm() <= eps2*(params.norm() + eps2) ){cout << "stop because change in x is small" << endl;break;} VectorXd paramsNew(params.rows());paramsNew = params - step; //h_lm = -step;//compute f(x)obj = objF(input,output,params);//compute f(x_new)VectorXd obj_new = objF(input,output,paramsNew);double deltaF = Func(obj) - Func(obj_new);double deltaL = linerDeltaL(-1 * step, gradient, u);double roi = deltaF / deltaL;cout << "roi is : " << roi << endl;if(roi > 0){params = paramsNew;u *= max(1.0/3.0, 1-pow(2*roi-1, 3));v = 2;}else{u = u * v;v = v * 2;}cout << "u = " << u << " v = " << v << endl;iterCnt++;cout << "Iterator " << iterCnt << " times, result is :" << endl << endl;}
}Dog-Leg代码:
void dogLeg(const VectorXd& input, const VectorXd& output, VectorXd& params)
{int errNum = input.rows(); //error numint paraNum = params.rows(); //parameter numVectorXd obj = objF(input, output, params);MatrixXd Jac = Jacobin(input, output, params); //jacobinVectorXd gradient = Jac.transpose() * obj; //gradient//initial parameter tao v epsilon1 epsilon2double eps1 = 1e-12, eps2 = 1e-12, eps3 = 1e-12;double radius = 1.0;bool found = obj.norm() <= eps3 || gradient.norm() <= eps1;if(found) return;double last_sum = 0;int iterCnt = 0;while(iterCnt < MAX_ITER){VectorXd obj = objF(input, output, params);MatrixXd Jac = Jacobin(input, output, params); //jacobinVectorXd gradient = Jac.transpose() * obj; //gradientif( gradient.norm() <= eps1 ){cout << "stop F'(x) = g(x) = 0 for a global minimizer optimizer." << endl;break;}if(obj.norm() <= eps3){cout << "stop f(x) = 0 for f(x) is so small";break;}//compute how far go along stepest descent direction.double alpha = gradient.squaredNorm() / (Jac * gradient).squaredNorm();//compute gauss newton step and stepest descent step.VectorXd stepest_descent = -alpha * gradient;VectorXd gauss_newton = (Jac.transpose() * Jac).inverse() * Jac.transpose() * obj * (-1);double beta = 0;//compute dog-leg step.VectorXd dog_leg(params.rows());if(gauss_newton.norm() <= radius)dog_leg = gauss_newton;else if(alpha * stepest_descent.norm() >= radius)dog_leg = (radius / stepest_descent.norm()) * stepest_descent;else{VectorXd a = alpha * stepest_descent;VectorXd b = gauss_newton;double c = a.transpose() * (b - a);beta = (sqrt(c*c + (b-a).squaredNorm()*(radius*radius-a.squaredNorm()))-c)/(b-a).squaredNorm();dog_leg = alpha * stepest_descent + beta * (gauss_newton - alpha * stepest_descent);}cout << "dog-leg: " << endl << dog_leg << endl;if(dog_leg.norm() <= eps2 *(params.norm() + eps2)){cout << "stop because change in x is small" << endl;break;}VectorXd new_params(params.rows());new_params = params + dog_leg;cout << "new parameter is: " << endl << new_params << endl;//compute f(x)obj = objF(input,output,params);//compute f(x_new)VectorXd obj_new = objF(input,output,new_params);//compute delta F = F(x) - F(x_new)double deltaF = Func(obj) - Func(obj_new);//compute delat L =L(0)-L(dog_leg)double deltaL = 0;if(gauss_newton.norm() <= radius)deltaL = Func(obj);else if(alpha * stepest_descent.norm() >= radius)deltaL = radius*(2*alpha*gradient.norm() - radius)/(2.0*alpha);else{VectorXd a = alpha * stepest_descent;VectorXd b = gauss_newton;double c = a.transpose() * (b - a);beta = (sqrt(c*c + (b-a).squaredNorm()*(radius*radius-a.squaredNorm()))-c)/(b-a).squaredNorm();deltaL = alpha*(1-beta)*(1-beta)*gradient.squaredNorm()/2.0 + beta*(2.0-beta)*Func(obj);}double roi = deltaF / deltaL;if(roi > 0){params = new_params;}if(roi > 0.75){radius = max(radius, 3.0 * dog_leg.norm());}else if(roi < 0.25){radius = radius / 2.0;if(radius <= eps2*(params.norm()+eps2)){cout << "trust region radius is too small." << endl;break;}}cout << "roi: " << roi << " dog-leg norm: " << dog_leg.norm() << endl;cout << "radius: " << radius << endl;iterCnt++;cout << "Iterator " << iterCnt << " times" << endl << endl;}
}main()
#include <eigen3/Eigen/Dense>
#include <eigen3/Eigen/Sparse>
#include <iostream>
#include <iomanip>
#include <math.h>using namespace std;
using namespace Eigen;const double DERIV_STEP = 1e-5;
const int MAX_ITER = 100;#define max(a,b) (((a)>(b))?(a):(b))int main(int argc, char* argv[])
{// obj = A * sin(Bx) + C * cos(D*x) - F//there are 4 parameter: A, B, C, D.int num_params = 4;//generate random data using these parameterint total_data = 100;VectorXd input(total_data);VectorXd output(total_data);double A = 5, B= 1, C = 10, D = 2;//load observation datafor (int i = 0; i < total_data; i++){//generate a random variable [-10 10]double x = 20.0 * ((random() % 1000) / 1000.0) - 10.0;double deltaY = 2.0 * (random() % 1000) /1000.0;double y = A*sin(B*x)+C*cos(D*x) + deltaY;input(i) = x;output(i) = y;}//gauss the parametersVectorXd params_gaussNewton(num_params);//init gaussparams_gaussNewton << 1.6, 1.4, 6.2, 1.7;VectorXd params_levenMar = params_gaussNewton;VectorXd params_dogLeg = params_gaussNewton;gaussNewton(input, output, params_gaussNewton);levenMar(input, output, params_levenMar);dogLeg(input, output, params_dogLeg);cout << "gauss newton parameter: " << endl << params_gaussNewton << endl << endl << endl;cout << "Levenberg-Marquardt parameter: " << endl << params_levenMar << endl << endl << endl;cout << "dog-leg parameter: " << endl << params_dogLeg << endl << endl << endl;
}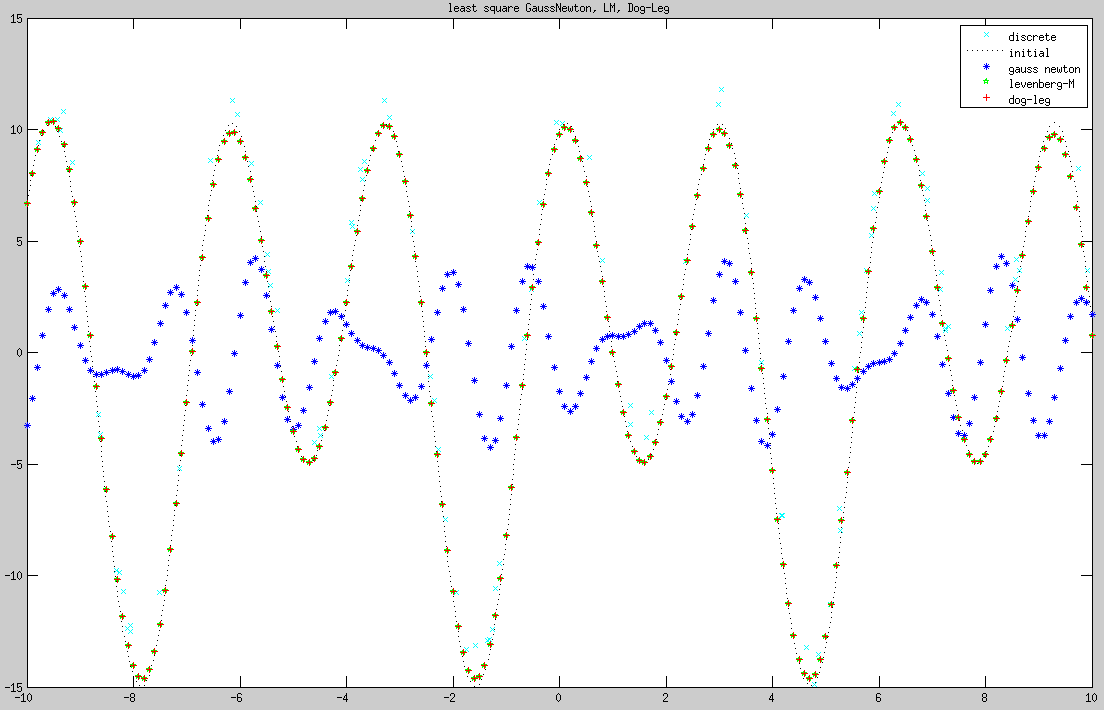
通常对于GaussNewton、LM、Dog-Leg,如果初始化的参数离真实值较近时,这三种方法都能收敛到真实值,而像例子中初始化参数 [1.6,1.4,6.2,1.7]T 与真实参数 [5,1,10,2]T 差距较大时,最后收敛的结果与真实值有一定的偏差。因为最小二乘法依赖于初始化参数,最后收敛的只能保证是一个极值点,但是不能保证是全局最优点,图中可以看到LM、Dog-Leg收敛的结果明显优于GaussNewton。
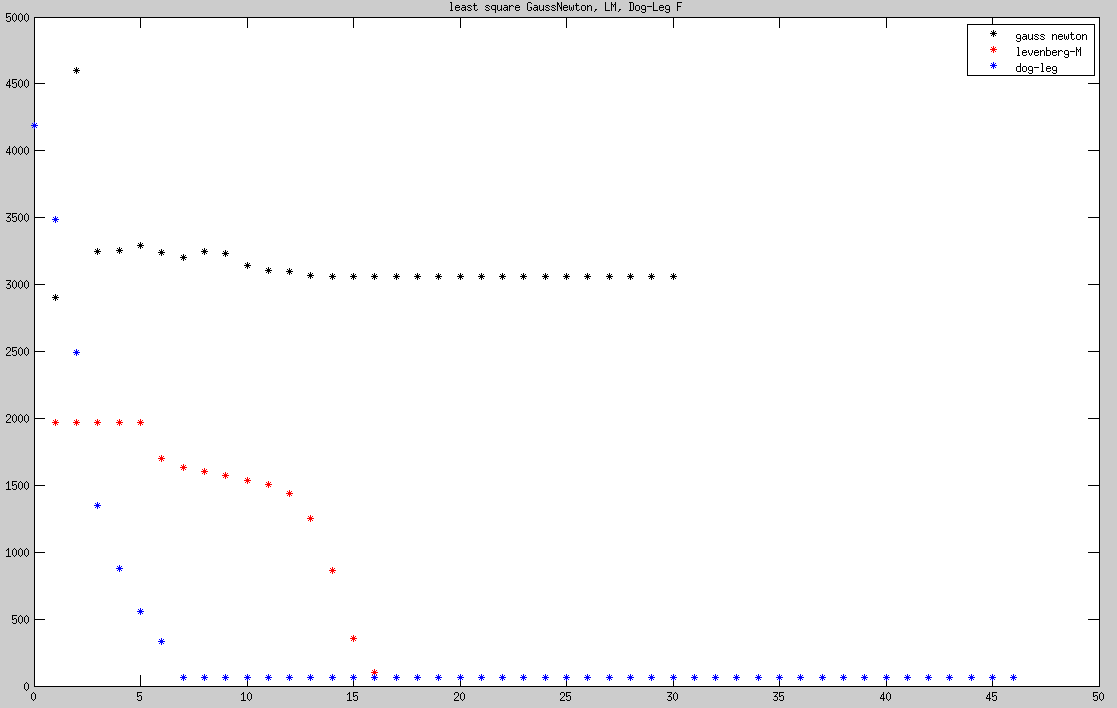
三种方法收敛过程中F值变化,可以看到LM、Dog-Leg收敛的结果明显优于GaussNewton。GaussNewton收敛过程中出现明显来回振荡,Dog-Leg最为平稳,LM收敛过程中出现三个阶段。
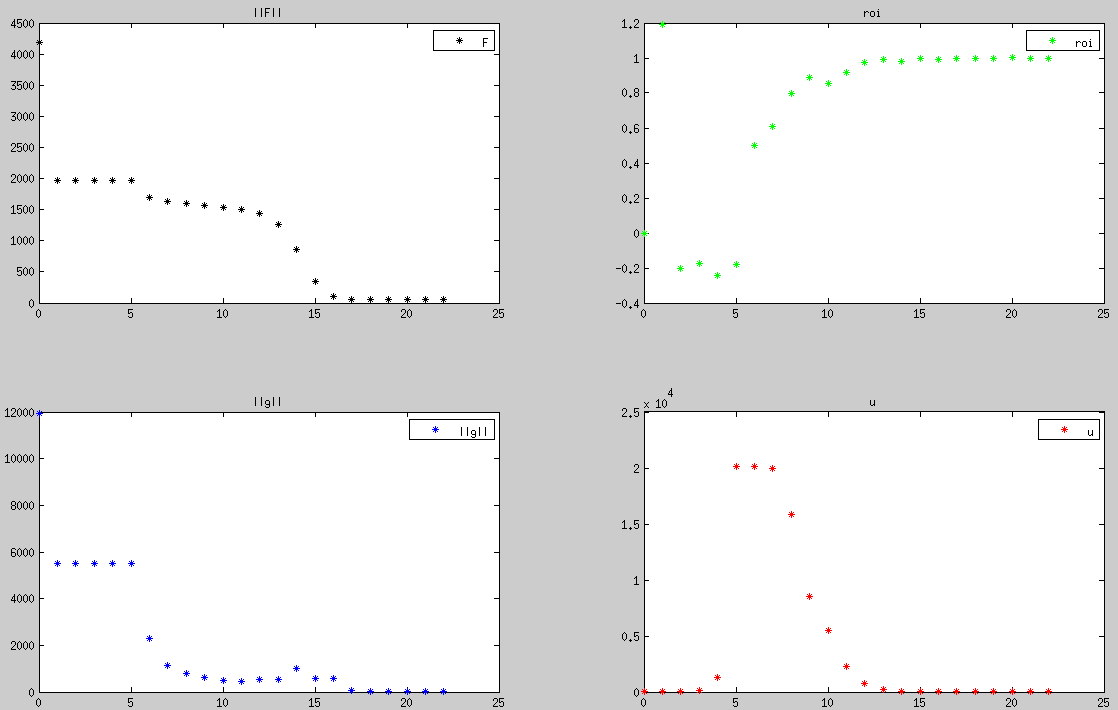
阻尼最小二乘法收敛过程中, F、∥g∥、u 的变化,可以看到在前5次迭代过程中,基本上GaussNewton方向占主导,但是 F 却出现略微增大情况,
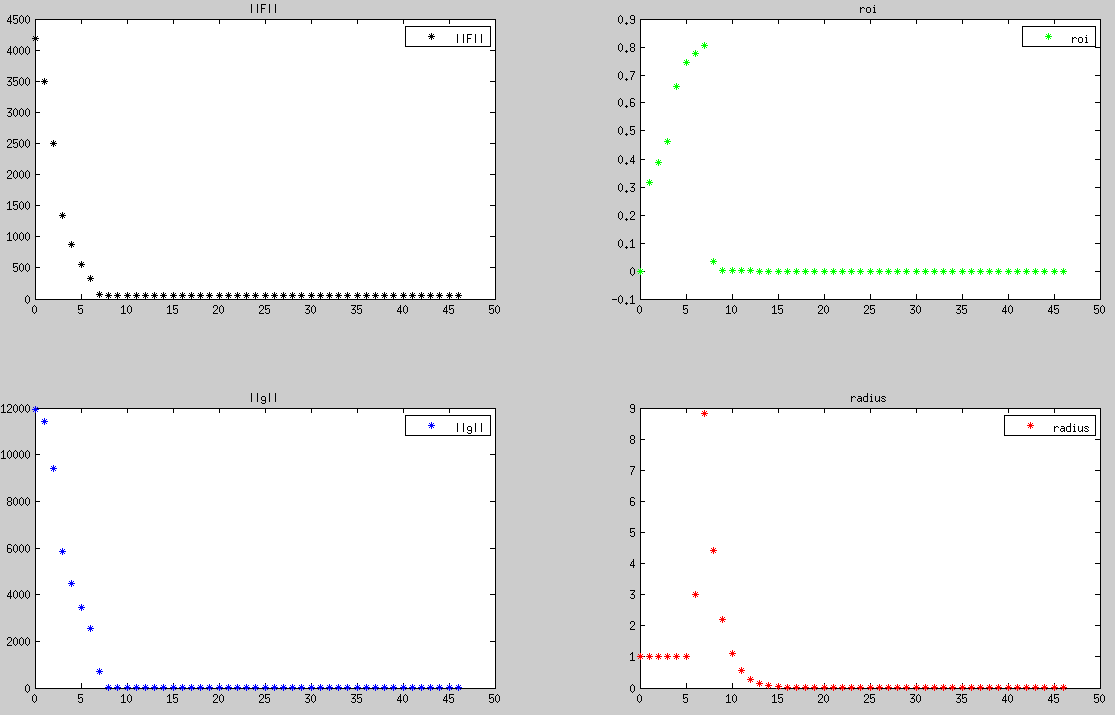
Dog-Leg收敛过程中trust region半径在不断改变,直到最后收敛后趋近于0。可以看到 radius 随着 ρ 增大而增大,而当 ρ 趋近于0时 radius 也收敛到0。
总结以上:
最小二乘法优化后结果依赖于初始值的选取,LM、Dog-Leg收敛结果明显好于GaussNewton。LM、Dog-Leg通常能够达到同样的收敛精度,综合来看Dog-Leg略优于LM。
这篇关于非线性最小二乘法之Gauss Newton、L-M、Dog-Leg的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



