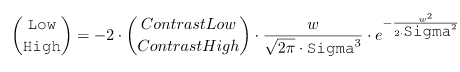gauss专题
Halcon提取边缘线段lines_gauss 算子
Halcon提取边缘线段lines_gauss 算子 edges_color_sub_pix和edges_sub_pix两个算子使用边缘滤波器进行边缘检测。还有一个常用的算子lines_gauss算子,也可以用于提取边缘线段,它的鲁棒性非常好,提取出的线段类型是亚像素精度的XLD轮廓。其原型如下: lines gauss(Image : Lines : Sigma, Low, High, Li
POJ2947 DAZE [Gauss]
题目是要求建立一个方程组: (mat[1][1]*x[1] + mat[1][2]*x[2] + … + mat[1][n]*x[n])%7 =mat[1][n+1] (mat[2][1]*x[1] + mat[2][2]*x[2] + … + mat[2][n]*x[n])%7 =mat[2][n+1] … … (mat[m][1]*x[1] + mat[m][2]*x[2
矩阵十题【三】 HDU 1588 Gauss Fibonacci
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1588 题目大意:先要知道一组斐波那契数列 i01234567f(i)011235813 下面给你一组数: k,b,n,M 现在知道一组公式g(i)=k*i+b;(i=0,1,2,3...n-1) 让你求出 f(g(i)) 的总和(i=01,2,3,...,n-1),比如给出的数据是
Centos服务器Open Gauss 部署
近期很多的项目由于信创要求使用一些国产的数据库,比如OpenGauss。OpenGuass是华为高斯DB的开源版,内核还是PostgreSQL,商业版是收费的。这里记录一下是如何安装部署 的。 官方中文文档 官方下载地址 部署要求 操作系统要求 ARM: openEuler 20.3LTS麒麟V10Asianux 7.5 X86: openEuler 20.3LTSCentOS 7.6As
Elasticsearch(9) gauss的使用
elasticsearch version: 7.10.1 在Elasticsearch中,gauss作为衰减函数(decay function)被用于function_score查询中,用于实现基于地理位置或其他数值字段的衰减权重评分。gauss衰减函数模拟了高斯分布,即距离中心点越近的文档,其得分越高;随着距离增大,得分按照高斯分布规律衰减。 gauss的语法 GET /your_inde
halcon line_gauss 线状物提取 (by shany shang)
主程序源代码: dev_close_window () *载入yi'fu'tu'xiang read_image (Angio, 'angio-part') get_image_size (Angio, Width, Height) dev_open_window (0, 0, 3 * Width / 2, 3 * Height / 2, 'black', WindowID) dev_disp
hdu 1588 Gauss Fibonacci 较难
对于Fib序列: (如果用F表示上市中的矩阵就有 F(n+1) = AF(n) 是等比数列,g(i)=k*i+b 是等差数列) F(g(i)) = F(b) + F(b+k)+F(b+2k)+....+F(b+nk) = F(b) + (A^k)F(b) + (A^2k)F(b)+….+(A^nk)F(b) 提取公因式 F(b) = F(b) [ E
高斯-塞德尔迭代法Gauss-Seidel_解线性方程组的迭代法
高斯-塞德尔迭代法Gauss-Seidel_解线性方程组的迭代法 标签:计算方法实验 #include <stdio.h>#include <math.h>#define maxn 3int main(){double a[maxn][maxn + 1], x[maxn] = {0};double eps = 1e-9;int n, k, kmax = 100;freopen("gauss
非线性最小二乘法之Gauss Newton、L-M、Dog-Leg
非线性最小二乘法之Gauss Newton、L-M、Dog-Leg 最快下降法 假设 hTF′(x)<0 h^TF'(x) < 0,则h是 F(x) F(x)下降方向,即对于任意足够小的 α>0 \alpha > 0,都满足 F(x+αh)<F(x) F(x+ \alpha h) < F(x)。 现在讨论 F(x) F(x)沿着h方向下降快慢: limα→0F(x)−F(x+αh)
MATLAB入门学习-#6-Jacobi、Gauss-Seidel、SOR迭代法编程练习
MATLAB入门学习-#6-Jacobi、Gauss-Seidel、SOR迭代法编程练习 1.Jacobi迭代法2.Gauss-Seidel迭代法3.SOR迭代法(松弛法) 这三种迭代法是在数值分析课程里学到的,都是求解线性方程组用的,相关的知识可以在数值计算方法的第三章里面找,可以说已经把最核心的怎么算和为什么这么算给交代了,剩下的任务就仅仅是编程实现就完了。 毕竟自己也没怎么
【华为GAUSS数据库】从0到1,数据库连接,新建用户,新建数据库,新建表等简单使用
数据库版本:GAUSSDB for opengauss, 集中式。 如果是新手,跳过这一part,直接看下一part。 若已知用户user,密码mypassword,数据库mydb, 数据库IPmyip, 数据库端口 myport,则可以在任意一台安装了gsql的机器上连接该数据库。 gsql -h myip -p myport -U user -W 'mypassword' -d mydb
python生成随机数:uniform(), randint(), gauss(), expovariate()
1 模块:random内建模块,伪随机数生成器 使用Mersenne Twister的伪随机数生成器PRNG进行生成,它以一个确定的数字作为属于,并为其生成一个随机数;为了安全起见,不要用PRNG生成随机数,要用secrets模块的真随机数TRNG生成; 2 播种随机数,即用随机数种子seed控制随机数 >>> import random## 1、当不指定种子seed时,PRNG每次生成的
高斯消元法(Gauss Elimination)【超详解模板】
高斯消元法,是线性代数中的一个算法,可用来求解线性方程组,并可以求出矩阵的秩,以及求出可逆方阵的逆矩阵。高斯消元法的原理是:若用初等行变换将增广矩阵 化为 ,则AX = B与CX = D是同解方程组。 所以我们可以用初等行变换把增广矩阵转换为行阶梯阵,然后回代求出方程的解。 1、线性方程组 1)构造增广矩阵,即系数矩阵A增加上常数向量
poj 1222 EXTENDED LIGHTS OUT(Gauss)
题目:EXTENDED LIGHTS OUT 思路:30个变元,30个异或方程,把czyuan神的Gauss模板改一改 #include <cstdio>#include <iostream>#include <algorithm>#include <cmath>#include <cstring>using namespace std;const int maxn =
线性方程组的迭代法(Jacobi 迭代法和Gauss-Seidel 迭代法) C++代码
Jacobi 迭代法 #include <iostream>#include <cmath>#include <vector>using namespace std;// 定义方程组的系数矩阵和常数向量vector<vector<double>> A = {{20, 2, 3},{1, 8, 1},{2, -3, 15}};vector<double> b = {24, 12, 30};
Hdoj 1588 Gauss Fibonacci 【矩阵快速幂】
Gauss Fibonacci Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 2584 Accepted Submission(s): 1078 Problem Description Without expecting, Angel
【数值计算方法】Gauss消元法及其Python/C实现
文章目录 一、基础理论1. 线性方程组2. Gauss消元法的详细步骤3. 注意事项 二、具体计算过程1. 用Gauss 消元法求A的LU分解,并由此求解方程组 Ax =ba. 将A进行LU分解。b. 使用LU分解求解方程组Ax=b 三、代码实现1. Python代码实现2. C语言代码实现 Gauss消元法,也称为高斯消元法或高斯-约当消元法,是一种用于求解线性方程组的
【转】Gauss-Newton优化方法 含代码
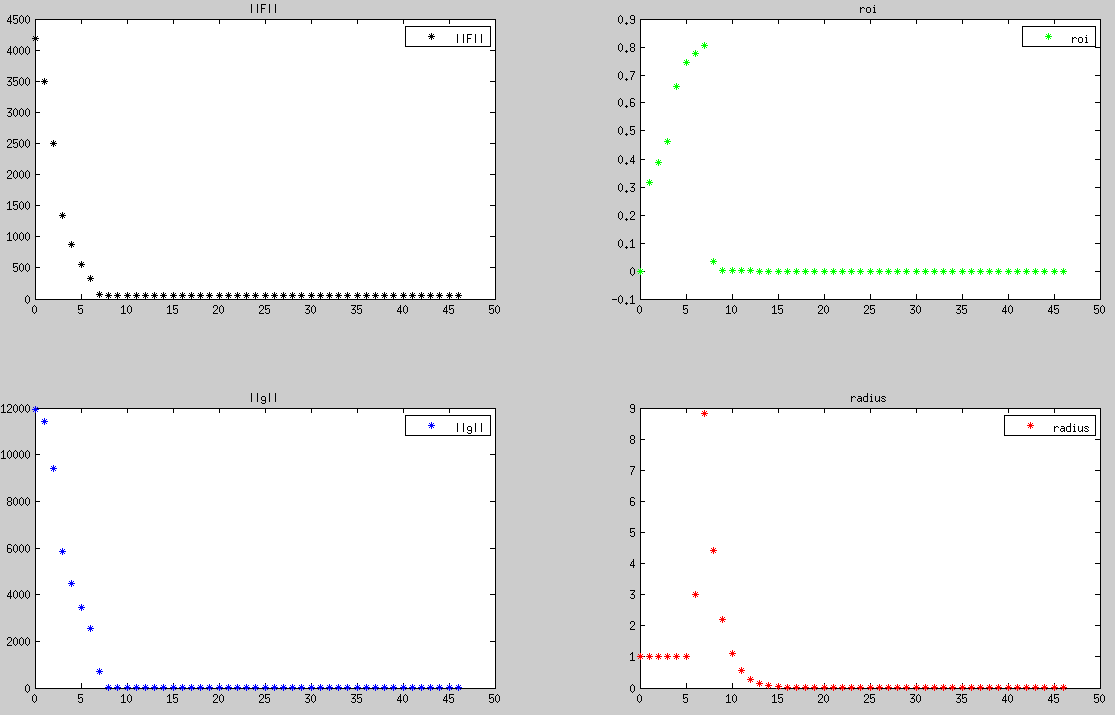
Gauss-Newton算法是解决非线性最优问题的常见算法之一,最近研读开源项目代码,又碰到了,索性深入看下。本次讲解内容如下: 基本数学名词识记牛顿法推导、算法步骤、计算实例高斯牛顿法推导(如何从牛顿法派生)、算法步骤、编程实例高斯牛顿法优劣总结 一、基本概念定义 1.非线性方程定义及最优化方法简述 指因变量与自变量之间的关系不是线性的关系,比如平方关系、对数关系
wgs84坐标系转化为中国大地坐标CGCS2000 / 3-degree Gauss-Kruger CM 120E
gps角分秒格式经纬度转double经纬度:getPosition方法 private static String getPosition(String position){String[] degree = position.split("\\°");if(degree.length == 1){return position;}String d = degree[0];String[]
【openGauss】启动异常 [GAUSS-53600] DETAIL: Permissions should be u=rwx (0700).
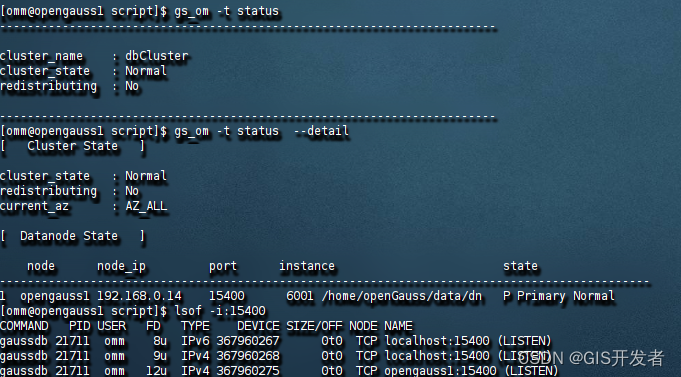
报错信息 [GAUSS-53600]: Can not start the database, the cmd is source /home/omm/.bashrc; python3 '/opt/software/om/script/local/StartInstance.py' -U omm -R /opt/software/install/app -t 300 --security-mod
第十六课:轮廓提取(threshold_sub_pix, bandpass_image, sobel_amp,lines_gauss)
1、threshold_sub_pix(Image : Border : Threshold : ) 阈值分割边缘提取 不经常使用 以灰度值大于Threshold区域和灰度值小于Threshold的区域为分界点提取亚像素精密轮廓 2、 3、 4 lines_gauss(Image : Lines : Sigma, Low, High, LightDark, Ex

![POJ2947 DAZE [Gauss]](/front/images/it_default.jpg)


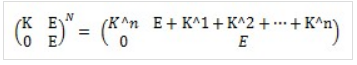


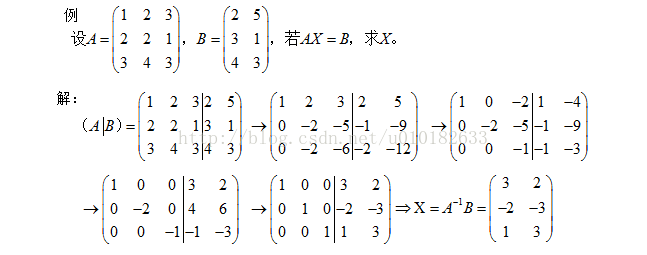

![【openGauss】启动异常 [GAUSS-53600] DETAIL: Permissions should be u=rwx (0700).](https://img-blog.csdnimg.cn/img_convert/d2efb8bd875196347cbb9cb7c8c80062.png)