本文主要是介绍hdu 1588 Gauss Fibonacci 较难,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
对于Fib序列:
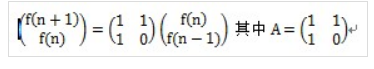
(如果用F表示上市中的矩阵就有 F(n+1) = AF(n) 是等比数列,g(i)=k*i+b 是等差数列)
F(g(i)) = F(b) + F(b+k)+F(b+2k)+....+F(b+nk)
= F(b) + (A^k)F(b) + (A^2k)F(b)+….+(A^nk)F(b)
提取公因式 F(b)
= F(b) [ E +A^k + A^2k + ….+ A^nk] (式中E表示的是单位矩阵)
令 K = A^k 后
E +A^k + A^2k + ….+ A^nk = K^0+K^1+K^2+…+K^n
构造矩阵
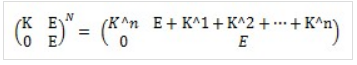
(不过这个图上的E+K^1.....K^n结果应该为E+K^1....k^n-1)
#include <iostream>
#include <string.h>
#include <cstdio>
#include <bits/stdc++.h>
#include <math.h>
using namespace std;
struct node
{long long martix[4][4];
}a,e,fb,ak,aa;
long long k,b,n,M;
int maxn;
void init()
{memset(a.martix,0,sizeof(a.martix));memset(e.martix,0,sizeof(e.martix));for(int i=0;i<maxn;++i)e.martix[i][i]=1;a.martix[0][0]=0;//a.martix[0][1]=a.martix[1][0]=a.martix[1][1]=1;
}
void INIT()
{memset(a.martix,0,sizeof(a.martix));memset(e.martix,0,sizeof(e.martix));for(int i=0;i<2;++i)for(int j=0;j<2;++j){a.martix[i][j]=ak.martix[i][j];}a.martix[0][2]=a.martix[1][3]=1;a.martix[2][2]=a.martix[3][3]=1;for(int i=0;i<4;++i)e.martix[i][i]=1;
}
node POW_mod(node a,node b)
{node ans;for(int i=0;i<maxn;++i)for(int j=0;j<maxn;++j){ans.martix[i][j]=0;for(int k=0;k<maxn;++k){if(a.martix[i][k]&&b.martix[k][j]){ans.martix[i][j]+=(a.martix[i][k]%M*b.martix[k][j]%M)%M;}}ans.martix[i][j]%=M;}return ans;
}
node martix_pow(int x)
{while(x){if(x&1)e=POW_mod(e,a);a=POW_mod(a,a);x>>=1;}return e;
}
int main()
{//freopen("in.txt","r",stdin);// freopen("out.txt","w",stdout);while(cin>>k>>b>>n>>M){maxn=2;init();fb=martix_pow(b);init();ak=martix_pow(k);maxn=4;INIT();aa=martix_pow(n);long long sum=0;sum+=(fb.martix[0][0]*aa.martix[0][3])%M+(fb.martix[0][1]*aa.martix[1][3]%M)%M;//这儿有点恶心 ,第一遍写的A=( 1,1 )// ( 1,0 ),样咧也过了,还是gg了,参考后改成A=( 0,1 )// ( 1,1 )就过了,......疑问//还有这儿为什么和aa.martix[0][3],aa.martix[1][3]相乘,而不是aa.martix[0][2],aa.martix[1][2].....疑问 cout<<sum%M<<endl;}return 0;
}
//用到了分块矩阵另一个递推
这篇关于hdu 1588 Gauss Fibonacci 较难的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



