过河专题
![笔试强训,[NOIP2002普及组]过河卒牛客.游游的水果大礼包牛客.买卖股票的最好时机（二)二叉树非递归前序遍历](https://i-blog.csdnimg.cn/direct/17efc4d0a1b749cb89ebdd715e23402b.png)
笔试强训,[NOIP2002普及组]过河卒牛客.游游的水果大礼包牛客.买卖股票的最好时机（二)二叉树非递归前序遍历
目录 [NOIP2002普及组]过河卒 牛客.游游的水果大礼包 牛客.买卖股票的最好时机（二) 二叉树非递归前序遍历 [NOIP2002普及组]过河卒 题里面给的提示很有用，那个马的关系，后面就注意，dp需要作为long的类型。 import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息publ
A*算法解决传教士—野人过河问题
A*算法解决传教士—野人过河问题 算法原理 1、A算法的基本原理分析； 在或图的一般搜索算法中，如果在搜索过程的步骤⑦利用估价函数f(n)=g(n)+h(n)对open表中的节点进行排序，则该搜索算法为A算法。 g(n)：从初始节点到n的实际代价 因为n为当前节点，搜索已达到n点，所以g(n)可计算出。 h(n)：启发函数，从n到目标节点的最佳路径的估计代价。 因为尚未找到解路径，所以h(n)
过河卒---记忆化搜索
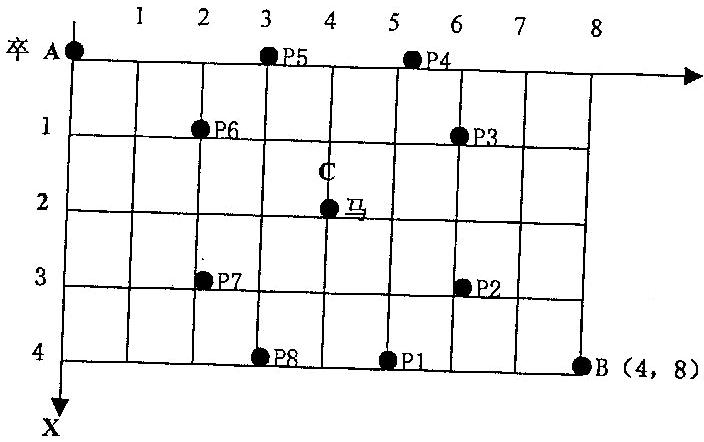
题目描述 Description 如图，A 点有一个过河卒，需要走到目标 B 点。卒行走规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马（如上图的C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图 C 点上的马可以控制 9 个点（图中的P1，P2 … P8 和 C）。卒不能通过对方马的控制点。 棋盘用坐标表示，A 点（0，0）、B 点（n,m）(n,
趣味算法------过河卒
目录 编辑 题目描述 解题思路 具体代码 总结 问题描述： 解决方案： 代码实现： 关键点： 题目描述 棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。 棋盘用坐标表示，A 点(0,0) 、B 点(n
【C++贪心】2498. 青蛙过河 II
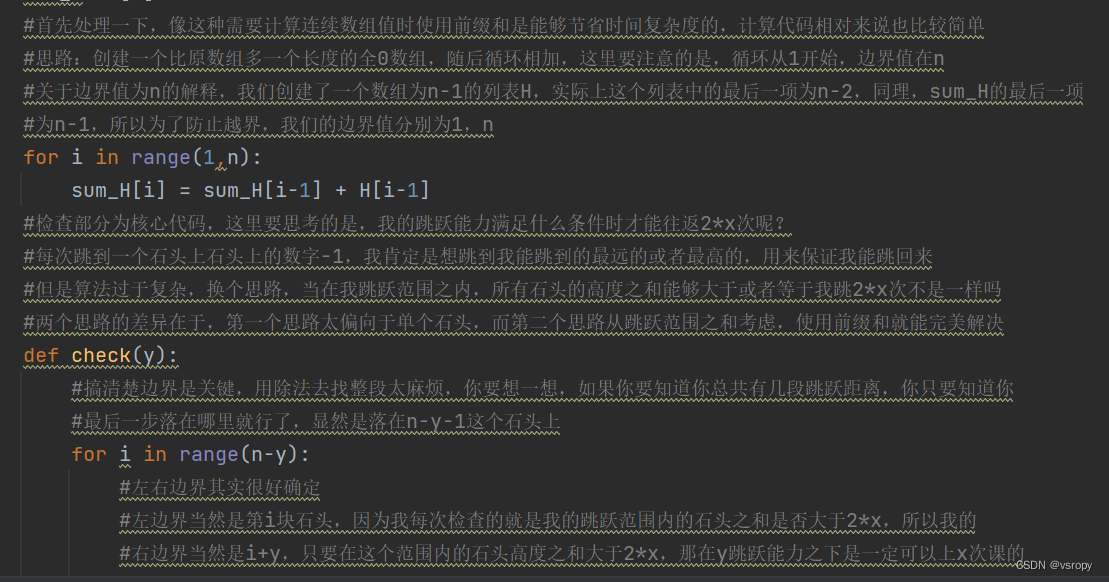
本文涉及知识点 贪心 优化后不需要二分 LeetCode2498. 青蛙过河 II 给你一个下标从 0 开始的整数数组 stones ，数组中的元素 严格递增 ，表示一条河中石头的位置。青蛙一开始在第一块石头上，它想到达最后一块石头，然后回到第一块石头。同时每块石头 至多 到达 一次。 一次跳跃的 长度 是青蛙跳跃前和跳跃后所在两块石头之间的距离。 更正式的，如果青蛙从 stones[i]
poj 2573 Bridge(贪心：过河问题)
开始以为排完序每次直接取相邻的就可以了呢 还以为是考察数据结构的题 WA了之后看别人的题解才知道这是一类问题 在这道题目中分析4个人 “a b c d” 过河情况： 把多种情况列出来会发现只有两种情况可能是最优的 第一种：最快的带最慢的 a c a a d a 第二种：最快的带最慢的和次快的带次慢的 a b a c d b 对于n > 3按照上面策略多次处理，每次可以
1224 - 过河卒
题目描述 AA 点有一个过河卒，需要走到目标 BB 点。 卒行走规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马（如下图的 CC 点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点。 例如：下图 CC 点可以控制 99 个点（图中的 P1,P2 \dots P8P1,P2…P8 和 CC ），卒不能通过对方马的控制点。 棋盘用坐标表示，现给定 AA 点位置为 (0,0)(
NYOJ,47,过河问题
过河问题 时间限制：1000 ms | 内存限制：65535 KB 难度：5 描述 在漆黑的夜里，N位旅行者来到了一座狭窄而且没有护栏的桥边。如果不借助手电筒的话，大家是无论如何也不敢过桥去的。不幸的是，N个人一共只带了一只手电筒，而桥窄得只够让两个人同时过。如果各自单独过桥的话，N人所需要的时间已知；而如果两人同时过桥，所需要的时间就是走得比较慢的那个人单独行动时所需的时间。问
2002NOIP普及组真题 4. 过河卒
线上OJ 地址： 【02NOIP普及组】过河卒 核心思想： 对于此类棋盘问题，一般可以考虑 dp动态规划、dfs深搜 和 bfs广搜。 解法一：dp动态规划 方法：从起点开始逐步计算到达每个位置的路径数。对于每个位置，它的路径数 等于 左边和上边位置的路径数之和（如果存在的话），同时要考虑到不能走被禁止的位置。 状态转移方程： d p [ i ] [ j ] = d p [ i −
【面试】Liveramp 面试题 面经 猴子过河问题
题目和青蛙过河有一点不同，A数组值是时间，因为我们需要按时间先后来处理，因此首先想到对值排序，但是复杂度会是nlogn，与题目不和。再看题目要求空间是哦（N+MAX(A)),因此可以新建一个数组，size为maxA，那么直接把值和索引兑换一下，空间换时间，就是On级别了。之后与青蛙过河完全相同。 public int monkeyCross(int D, int[] A, int N){
【面试】Liveramp 面试题 面经 青蛙过河问题
题目如上图所示，截取自http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=142004&highlight=liveramp 说下自己的思路，首先可以肯定的是需要遍历时间数组。每一个时间看一下能否到达。 第一个思路是用backtracking，每一个时间检测一次，时间复杂度基本是O（DN^2）。事实上，对于线性的所搜或
第十三届蓝桥杯真题：x进制减法，数组切分，gcd，青蛙过河
目录 x进制减法 数组切分 gcd 青蛙过河 x进制减法 其实就是一道观察规律的题。你发现如果a这个位置上的数x，b这个位置上的数是y，那么此位置至少是max(x,y)+1进制。一定要把位置找对啊 #include <bits/stdc++.h>using namespace std;typedef long long ll;
NYOJ 47 - 过河问题
描述 在漆黑的夜里，N位旅行者来到了一座狭窄而且没有护栏的桥边。如果不借助手电筒的话，大家是无论如何也不敢过桥去的。不幸的是，N个人一共只带了一只手电筒，而桥窄得只够让两个人同时过。如果各自单独过桥的话，N人所需要的时间已知；而如果两人同时过桥，所需要的时间就是走得比较慢的那个人单独行动时所需的时间。问题是，如何设计一个方案，让这N人尽快过桥。 输入 第一行是一个整数T(1<
洛谷p1002过河卒
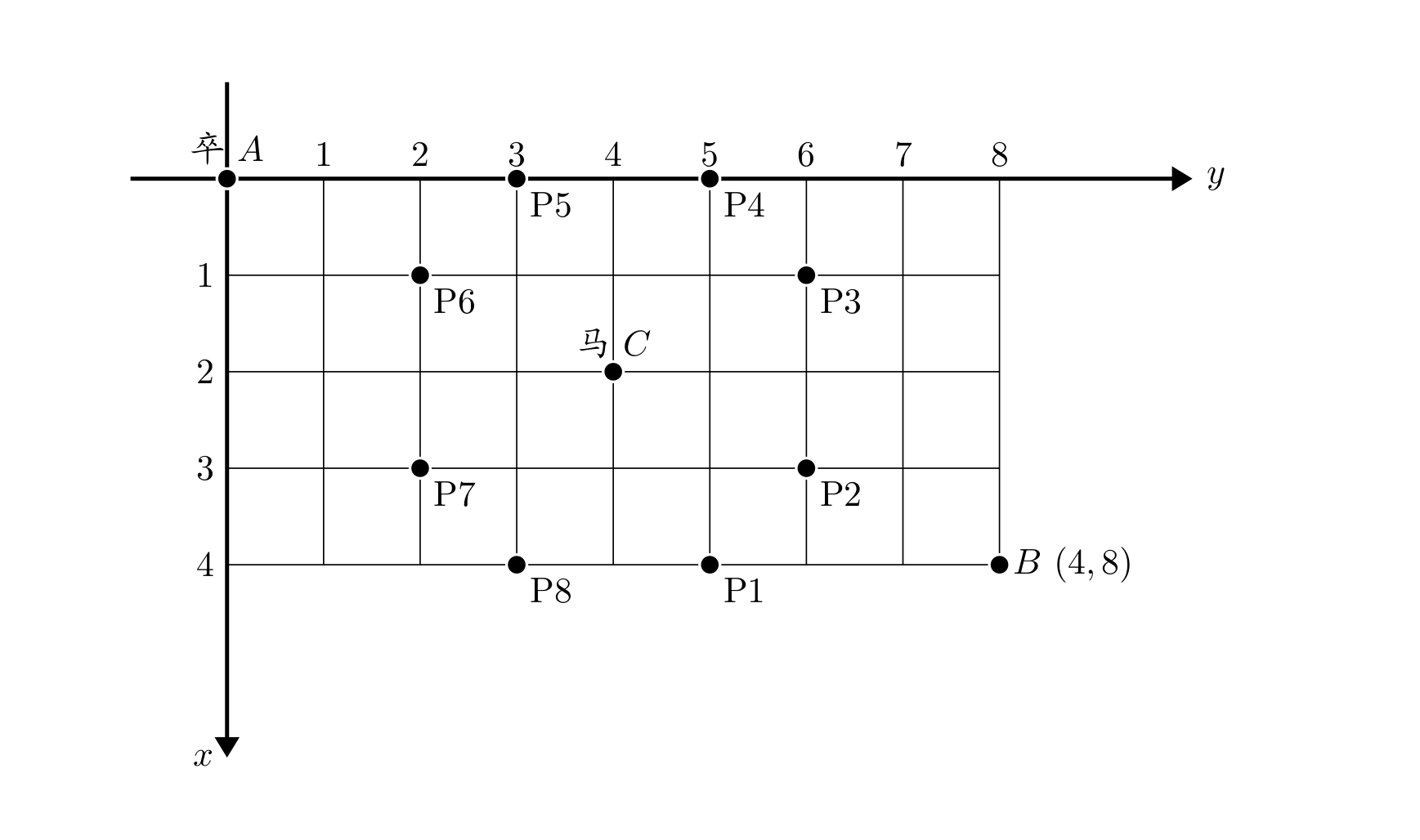
[NOIP2002 普及组] 过河卒 题目描述 棋盘上 A A A 点有一个过河卒，需要走到目标 B B B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C C C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。 棋盘用坐标表示， A A A 点 ( 0 , 0 ) (0, 0) (0,0)、 B B B 点 ( n ,
《算法的乐趣》6.妖怪和和尚过河问题------python
文章目录 问题描述状态和动作关键 问题描述 有三个和尚和三个妖怪要利用唯一一条小船过河，这条小船一次最多载两个人。同时，无论在河两岸还是在船上，只要妖怪的数量大于和尚的数量，妖怪就会将和尚吃掉。安排一下，保证和尚和妖怪都能过河并且和尚不能被妖怪吃掉。 方法类似于第五章的内容：遍历所有由妖怪、和尚和小船的位置构成的状态空间，寻找一条或多条从初始状态到最终状态的转换路径。结果
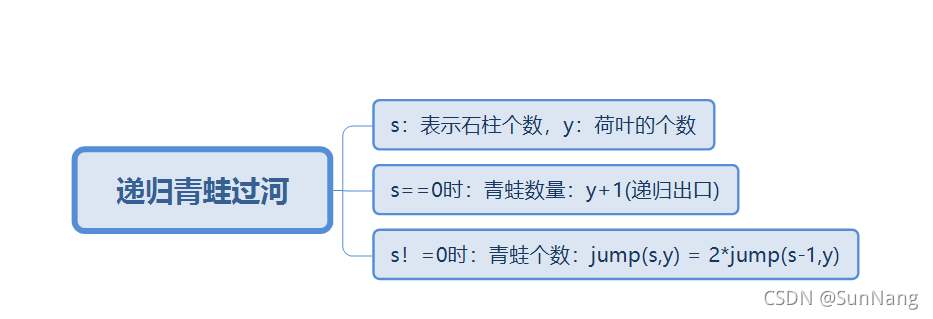
C语言 青蛙过河问题
#include<stdio.h> /*递归出口s==0（判断条件），初始值s，y由用户输入（初始值），s-1赋值给s（步长值）*/int fun(int s,int y){if(s==0)//递归出口，当石柱个数等于0时 {return y+1;//青蛙个数==荷叶个数+1 }else{return 2*fun(s-1,y);//有石柱和荷叶的情况下满足：jump(s,y)
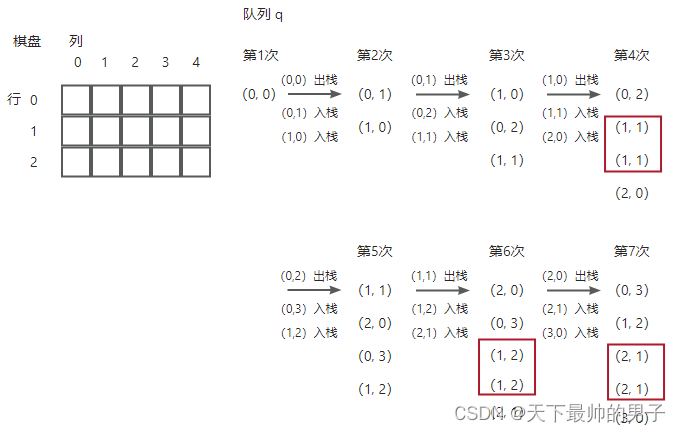
农夫过河问题-广度优先搜索-逻辑运算
辣鸡小玲的题解 冯向阳老师的数据结构-队列 农夫过河，上题目： 题目 然后贴代码 #include <iostream>#include <cstdlib>#include <cstdio>#include <string>#include <sstream>using namespace std;const int MAXLISTSIZE = 100;te
每日力扣：403. 青蛙过河
package com.sample.suncht.algo;import java.util.*;/*** 403. 青蛙过河* <p>* 一只青蛙想要过河。 假定河流被等分为 x 个单元格，并且在每一个单元格内都有可能放有一石子（也有可能没有）。 青蛙可以跳上石头，但是不可以跳入水中。* <p>* 给定石子的位置列表（用单元格序号升序表示）， 请判定青蛙能否成功过河（即能否在最后一步跳至最后一
1921：【02NOIP普及组】过河卒
1921：【02NOIP普及组】过河卒 【题目描述】 如图，A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。 同时在棋盘上的任一点有一个对方的马（如上图的C点），该马所在的点和所有跳跃一步可达的点称为方马的控制点。例如上图C点上的马可以控制9个点（图中的P1，P2…P8和C）。卒不能通过对方的控制点。 棋盘用坐标表示，A点（0，0）、B点（n, m）(n,m为不超过20
【洛谷_P1052】过河
过河 题目描述 在河上有一座独木桥，一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子，青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数，我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点：0,1,…,L（其中L是桥的长度）。坐标为0的点表示桥的起点，坐标为L的点表示桥的终点。青蛙从桥的起点开始，不停的向终点方向跳跃。一次跳跃的距离是S到T之间的任意正整数（
牛客算法入门DP：过河卒
0x00 题目来源 过河卒 经典! 0x10 Tag 线性dp 0x20 题目描述 棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。 棋盘用坐标表示，A 点 (0, 0) B 点 (n, m)，同样马的位置坐标是需要给出的。
C++面试宝典第24题：袋鼠过河
题目 一只袋鼠要从河这边跳到河对岸，河很宽，但是河中间打了很多桩子。每隔一米就有一个桩子，每个桩子上都有一个弹簧，袋鼠跳到弹簧上就可以跳得更远。每个弹簧力量不同，用一个数字代表它的力量，如果弹簧力量为5，就代表袋鼠下一跳最多能够跳5米；如果为0，就会陷进去无法继续跳跃。河流一共N米宽，袋鼠初始位置就在第一个弹簧上面，要跳到最后一个弹簧之后就算过河了。给定每个弹簧的力量，求袋鼠最少
![洛谷-P1002-[NOIP2002 普及组]-过河卒](https://img-blog.csdnimg.cn/img_convert/c3152aa0798200dbbb564fc5dad4b374.png)
洛谷-P1002-[NOIP2002 普及组]-过河卒
[NOIP2002 普及组] 过河卒 题目描述 棋盘上 A A A 点有一个过河卒，需要走到目标 B B B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C C C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。 棋盘用坐标表示， A A A 点 ( 0 , 0 ) (0, 0) (0,0)、 B B B 点 ( n ,