2002NOIP普及组真题 4. 过河卒

本文主要是介绍2002NOIP普及组真题 4. 过河卒，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

线上OJ 地址：

【02NOIP普及组】过河卒

核心思想：

对于此类棋盘问题，一般可以考虑 dp动态规划、dfs深搜 和 bfs广搜。

解法一：dp动态规划

方法：从起点开始逐步计算到达每个位置的路径数。对于每个位置，它的路径数 等于 左边和上边位置的路径数之和（如果存在的话），同时要考虑到不能走被禁止的位置。
状态转移方程：$dp[i][j]=dp[i-1][j]+dp[i][j-1]$
状态初始化：

第0行只能从左边转移过来；
第0列只能从上面转移过来；
dp[0][0]为1，表示自己到自己有1种方法。

注意：计算马的屏蔽坐标时不要遗漏马本身
特别注意：虽然只有20个格子，但本题的结果数据很大。开 int 只能60分，需要 开 long long 方能100分。

题解代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;const int N = 25;
ll dp[N][N];  // 不开 long long 见祖宗 
bool hasBlock[N][N];  // hasBlock[i][j] 为true,表示该位置被马控制了，不能走 // 计算不能走的区域(本题为马的控制区域)
void cmp(int x, int y, int n, int m) 
{int dx[] = {1, 2, 2, 1, -1, -2, -2, -1};int dy[] = {2, 1, -1, -2, -2, -1, 1, 2};hasBlock[x][y] = true;  // 马本身的坐标屏蔽 for (int i = 0; i < 8; i++) {int nx = x + dx[i];int ny = y + dy[i];if (nx >= 0 && nx <= n && ny >= 0 && ny <= m)   hasBlock[nx][ny] = true;  // 马控制的8个区域不能走 }
}int main() 
{int n, m, x, y;scanf("%d %d %d %d", &n, &m, &x, &y);cmp(x, y, n, m);   // 先标记所有不能走的区域 memset(dp, 0, sizeof(dp));dp[0][0] = 1;  // 初始化第一个 for(int j = 1; j <= m; j++)  if(!hasBlock[0][j])  dp[0][j] = dp[0][j-1];  // 初始化第一行 for(int i = 1; i <= n; i++)  if(!hasBlock[i][0])  dp[i][0] = dp[i-1][0];  // 初始化第一列 for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) if (!hasBlock[i][j]) dp[i][j] = dp[i - 1][j] + dp[i][j - 1];  // 状态转移方程cout << dp[n][m] << endl;return 0;
}

解法二：dfs深搜

方法：dfs深搜的思路和动态规划类似。从起点开始向下深搜，令 dfs(x, y) 的返回值表示从(x, y)到终点的路径数，则 dfs(x, y) = dfs(x + 1, y) + dfs(x, y + 1);
即 (x, y)到终点的 路径数 等于 它 右边和下边位置的路径数之和（如果存在的话），同时要考虑到不能走被禁止的位置。
注意：为了减少重复计算，采用 记忆化搜索，即
$f[x][y]=dfs(x+1,y)+dfs(x,y+1);returnf[x][y];$

这样下一次再深搜到 (x, y)时，可以直接返回f[x][y]，不需要再继续dfs。
特别注意：因为 dfs(x, y) 有返回值，所以 dfs 的返回值 类型同样不能是 int，要 开成 long long ，否则只有60%分数。

题解代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;const int N = 25;
int n, m, x, y; 
ll f[N][N];  // 不开 long long 见祖宗; f[i][j] 表示从(i, j)走到(n, m)需要的步数 
bool hasBlock[N][N] = {0}; // 标记已访问的点// 深度优先搜索函数
ll dfs(int x, int y)     // 此处要用到dfs的返回值，不开 long long 见祖宗 
{if(f[x][y] != 0)  return f[x][y];   // 记忆化搜索。算过的就不要再算了 if(x == n && y == m) // 如果到了终点，就返回1，表示有一种方案 return 1;if(hasBlock[x][y] || x > n || y > m) // 遇到不可行的点，返回0，表示无方案 return 0;// 本题只能向右和向下，不存在回路，所以不需要visit数组标记是否访问过 f[x][y] = dfs(x + 1, y) + dfs(x, y + 1); // 向下移动 +向右移动return f[x][y];
}void cmp(int x, int y, int n, int m) 
{int dx[] = {1, 2, 2, 1, -1, -2, -2, -1};int dy[] = {2, 1, -1, -2, -2, -1, 1, 2};hasBlock[x][y] = true;  // 马本身的坐标屏蔽 for (int i = 0; i < 8; i++) {int nx = x + dx[i];int ny = y + dy[i];if (nx >= 0 && nx <= n && ny >= 0 && ny <= m)   hasBlock[nx][ny] = true;  // 马控制的8个区域不能走 }
}// dfs
int main() 
{scanf("%d %d %d %d", &n, &m, &x, &y);cmp(x, y, n, m);   // 计算不能走的区域 memset(f, 0, sizeof(f));  // 初始化 cout << dfs(0, 0);return 0;
}

解法三：bfs广搜

方法：从起点(0, 0)开始向右（向下）广搜。令 f[i][j] 表示从(0, 0)走到(i, j)的方案数，则 f[n][m]就是最终要输出的方案数。
我们知道，任何一个坐标要么从上面过来，要么从左面过来（如果存在的话，同时要考虑到不能走被禁止的位置）。所以走到当前位置的方案总数，是走到上面位置的方案总数 + 走到左边位置的方案总数。
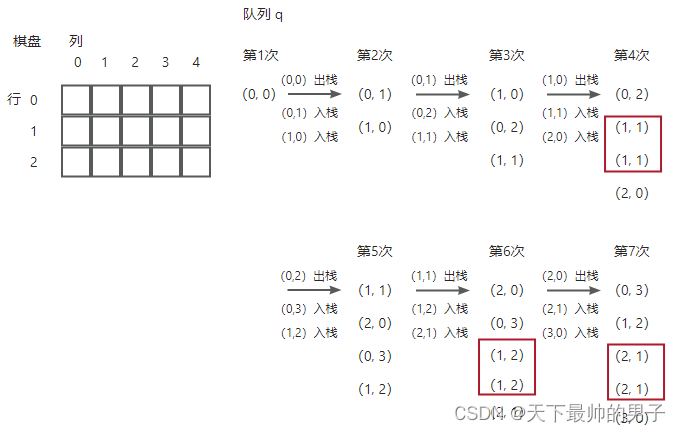
核心：在将某个坐标加入广搜队列之前，要先判断该坐标是否已经在队列中。如果不在，就加入队列。如果已经在，就不要重复入队列，只需要更新该(i, j)的 f[i][j] 即可。这样一来，当(i , j)从队列中弹出并参与向后传递时，f[i][j] 的数值是完整的。

我们可能会担心：(i, j) 上一次入队已经出队了，那判断(i, j)是否在队列中是否还有意义。
我们简单模拟一下队列里面的坐标，如下图所示。会发现在栈中，第二次(i, j) 入队列时，第一个(i, j) 还没出队。所以，上述担心不存在。

#include <bits/stdc++.h>
#define ll long long
using namespace std;typedef pair<int, int> PII;
const int N = 25;int n, m;
ll f[N][N];  // 不开 long long 见祖宗 ; f[i][j] 表示从(0, 0)走到(i, j)的方案数 
bool hasBlock[N][N] = {0}; // 标记已访问的点
bool vis[N][N];  // vis[i][j]=true表示坐标(i, j)已经在队列中。用于控制同一个坐标不要重复出现在队列里 // 深度优先搜索函数
void bfs(int a, int b)     // 此处要用到dfs的返回值，不开 long long 见祖宗 
{int dx[] = {1, 0};  // 向右和向下的移动方向int dy[] = {0, 1};queue<PII> q;f[0][0] = 1;  // 初始化，从(0, 0)走到(0, 0)有1种方案 vis[0][0] = true;q.push({0, 0});while (!q.empty()) {PII u = q.front();q.pop();int x = u.first;int y = u.second;for (int i = 0; i < 2; i++) {   // 只能向右和向下int nx = x + dx[i], ny = y + dy[i];if (nx >= 0 && nx <= n && ny >= 0 && ny <= m && !hasBlock[nx][ny]) {if (vis[nx][ny] == false) // 如果下一个坐标还没入队列 {vis[nx][ny] = true; f[nx][ny] = f[x][y];  // 则走到当前坐标的方案数就是走到下一个坐标的方案数 q.push({nx, ny});     // 将下一个坐标入队列 } else f[nx][ny] += f[x][y]; // 如果下一个坐标已经在队列中，则不重复入队列，但是需累加当前坐标的方案数}}}	
}void cmp(int x, int y, int n, int m) 
{int dx[] = {1, 2, 2, 1, -1, -2, -2, -1};int dy[] = {2, 1, -1, -2, -2, -1, 1, 2};hasBlock[x][y] = true;  // 马本身的坐标屏蔽 for (int i = 0; i < 8; i++) {int nx = x + dx[i];int ny = y + dy[i];if (nx >= 0 && nx <= n && ny >= 0 && ny <= m)   hasBlock[nx][ny] = true;  // 马控制的8个区域不能走 }
}// bfs
int main() 
{int x, y;scanf("%d %d %d %d", &n, &m, &x, &y);cmp(x, y, n, m);   // 计算不能走的区域 memset(f, 0, sizeof(f));  // 初始化 bfs(0, 0);cout << f[n][m];return 0;
}

这篇关于2002NOIP普及组真题 4. 过河卒的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---