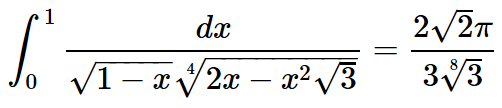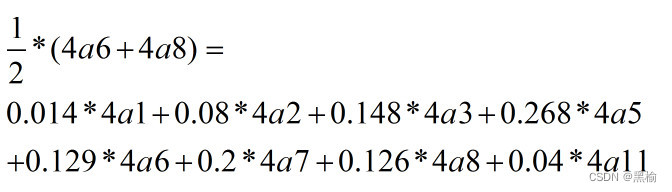等式专题

等式（数论/唯一分解定理）

链接： https://www.nowcoder.com/acm/contest/90/F 来源：牛客网题目描述给定n，求1/x + 1/y = 1/n （x<=y）的解数。（x、y、n均为正整数）输入描述: 在第一行输入一个正整数T。接下来有T行，每行输入一个正整数n，请求出符合该方程要求的解数。（1<=n<=1e9）输出描述: 输出符合该方程要求的解数。

P1149 [NOIP2008 提高组] 火柴棒等式(一个比较有意思的题)

P1149 [NOIP2008 提高组] 火柴棒等式 #include <bits/stdc++.h>using namespace std;int n, ans, a[11111]={6, 2, 5, 5, 4, 5, 6, 3, 7, 6};bool vis[11111][11111];int main(){cin >> n;//计算每个数需要的火柴棒for(int i=10;

整型数组处理算法（八）插入（+、-、空格）完成的等式：1 2 3 4 5 6 7 8 9=N[华为面试题]

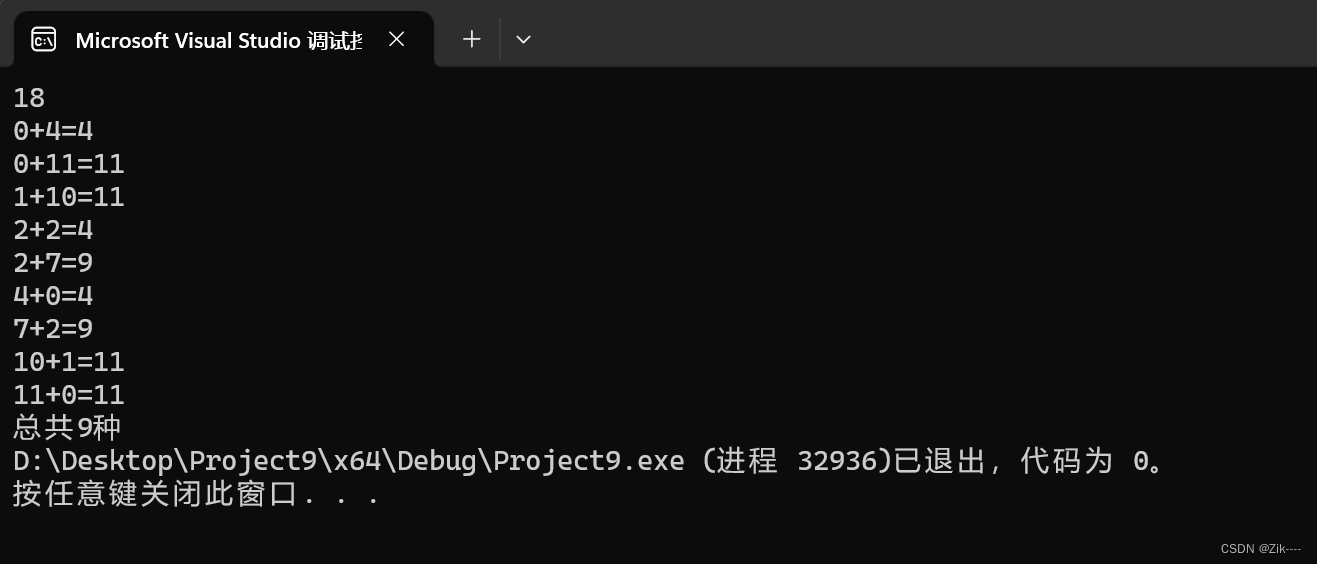
转载自有一个未完成的等式：1 2 3 4 5 6 7 8 9=N 当给出整数N的具体值后，请你在2，3，4，5，6，7，8，9这8个数字的每一个前面，或插入运算符号“+”，或插入一个运算符号“-”，或不插入任何运算符号，使等式成立，并统计出能使等式成立的算式总数，若无解，则输出0。例如：取N为108时，共能写出15个不同的等式，以下就是其中的二个算式： 1+23+4+56+7+8+9=10

fzu——Problem 2125 简单的等式

Problem Description 现在有一个等式如下：x^2+s(x,m)x-n=0。其中s(x,m)表示把x写成m进制时，每个位数相加的和。现在，在给定n，m的情况下，求出满足等式的最小的正整数x。如果不存在，请输出-1。 Input 有T组测试数据。以下有T(T<=100)行，每行代表一组测试数据。每个测试数据有n（1<=n<=10^18），m(2<=m<=16)。

假设在n进制下，下面的等式成立，n值是（） 567*456=150216 9 10 12 18

假设在n进制下，下面的等式成立，n值是（） 567*456=150216 9 10 12 18 假设n进制，则有(5*n 2 +6*n+7) * (4*n 2 +5*n+6) = n 5 +5*n 4 +2*n 2 +n+6，简化以后可以得到 15*n4+49*n3+86*n2+70*n+36=n5,两边同时除以n5，可以得到15/n+49/n2+86/n3+70/

火柴棍等式--枚举

火柴棍等式要求用m(m <= 24)根火柴棍拼出A+B=C的等式，数字非零，则最高位不能是0，加号和等号各用了两根火柴棍，问可以拼出多少个不同等式？思路枚举法代码 #include <stdio.h>#define M 18int fun(int x) {int a[10] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6};int sum = 0;while(

编写一个应用程序，验证以下等式是成立的：

编写一个应用程序，验证以下等式是成立的：提示：if分支语句、for循环语句与C、C++是一样的。如果能完成上面的验证，则达到基本要求（可得到基本分数8分）。较高要求，可根据实际情况选做(可得到附加的2分）：找到更多的这样的整数：一些相续正整数的立方和正好等于另一个整数的立方。初学JAVA，编写程序可以验证题目中两个等式成立，简单的验证了上述题目中两个等式的成立，以变量cnt为验

C/C++火柴棍等式

有n根(n<=24)火柴棍，你可以拼出多少个形如“A+B=C"的等式?等式中的A、B、C是用火柴棍拼出的整数(若该数非零，则最高位不能是0)。用火柴棍拼数字0-9的拼法如图所示: 依次需要用到的火柴棍数目为6 2 5 5 4 5 6 3 7 6 。如果是初学者可能会这么写。 int main() {int a[10];int b, i, j, k;for (b = 0; b

【中国大学MOOC】java程序设计-week2-编写一个应用程序，验证以下等式是成立的

1.题目编写一个应用程序，验证以下等式是成立的：提示：if分支语句、for循环语句与C、C++是一样的。如果能完成上面的验证，则达到基本要求（可得到基本分数8分）。较高要求，可根据实际情况选做(可得到附加的2分）：找到更多的这样的整数：一些相续正整数的立方和正好等于另一个整数的立方。 2.题解验证不等式是否成立，直接按照题目要求编写即可；扩展要求：设定最大值数量为30

POJ 1183 / Noi 01 反正切函数的应用 (等式变形能否有比O(a)更快的算法？)

反正切函数的应用 Time Limit: 1000MS Memory Limit: 10000K http://poj.org/problem?id=1183 由题意得等式 (c-a)(b-a)=a2+1 (注意xy+Dx+Ey+F=0的等式都可以化为(x+E)(y+D)=DE-F的形式) 然后令

关于n进制数等式成立时的n值问题

声明：本文暂时只讨论算法，不做代码实现问题有些抽象不好描述，所以先引用一道阿里巴巴笔试题说明（）进制下，下面等式成立 567*456=150216 A.9 B.10 C.12 D.18 方法一：看尾数7*6=42;42%n=6;对照选项带出答案C,D 然后计算十进制567*456=258552；结果比150216大很多，排除12进制，大致估算选D方法二：(5*

全面解析企业财务报表系列之二：财务状况等式

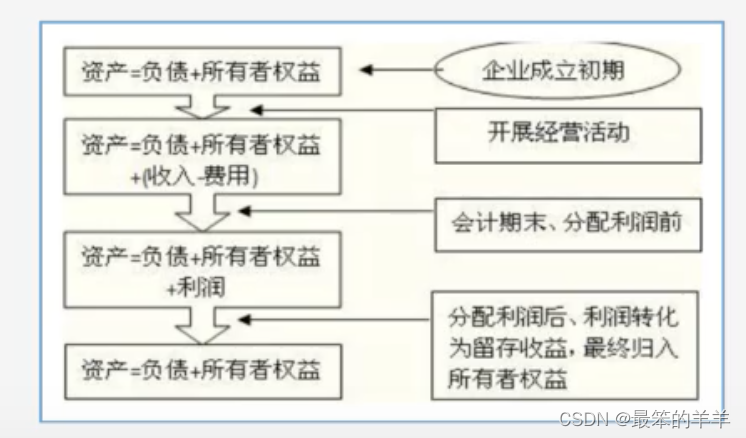
全面解析企业财务报表系列之二：财务状况等式一、财务状况等式二、会计恒等式三、复试记账法四、经营成果等式五、第三会计等式一、财务状况等式会计恒等式复试记账法权责发生制二、会计恒等式资产=负债+所有者权益三、复试记账法每笔交易至少在两个账户中记录资产=负债+所有者权益四、经营成果等式动态会记等式，是用以反应企业一定时期收入、费用和利润之间恒等关系

立方和等式

考虑方程式：a^3 + b^3 = c^3+ d^3 其中：“^”表示乘方。a、b、c、d是互不相同的小于30的正整数。这个方程有很多解。比如： a = 1，b=12，c=9，d=10 就是一个解。因为：1的立方加12的立方等于1729，而9的立方加10的立方也等于1729。当然，a=12，b=1，c=9，d=10 显然也是解。如果不计abcd交换次序的情况，这算同一个解。你的

P1149 火柴棒等式（打表暴力暴力出奇迹）

给你n根火柴棍，你可以拼出多少个形如“A+B=CA+B=C”的等式？等式中的AA、BB、CC是用火柴棍拼出的整数（若该数非零，则最高位不能是00）。用火柴棍拼数字0-90−9的拼法如图所示：注意： 1加号与等号各自需要两根火柴棍 2如果A≠BA≠B，则A+B=CA+B=C与B+A=CB+A=C视为不同的等式(A,B,C>=0A,B,C>=0) 3nn根火柴棍必须全部用上输入输出格式

【RL】Bellman Equation （贝尔曼等式）

Lecture2: Bellman Equation State value 考虑grid-world的单步过程： S t → A t R t + 1 , S t + 1 S_t \xrightarrow[]{A_t} R_{t + 1}, S_{t + 1} StAt Rt+1,St+1 t t t, t + 1 t + 1 t+1：时间戳 S t S_t St：时间

谁能证明这道积分等式题?微积分的知识都忘光了

证明左边的定积分结果是右边的值;

一个定积分等式的证明

问题证明一个定积分恒等式： I=∫+∞0x3ex−1dx=π415 I=\int_0^{+\infty}\frac{x^3}{e^x-1}{\rm{d}}x=\frac{\pi^4}{15} 证明两种方法证明(实际是一种)。 1.利用 Γ \Gamma函数和黎曼 ζ \zeta函数关系等式从维基百科上黎曼 ζ \zeta函数词条可以看到黎曼 ζ \zeta函数的这

【模拟】火柴棒等式

题目描述给你n根火柴棍，你可以拼出多少个形如“A+B=C”的等式？等式中的A、B、C是用火柴棍拼出的整数（若该数非零，则最高位不能是0）。用火柴棍拼数字0-9的拼法如图所示：注意： 1. 加号与等号各自需要两根火柴棍 2. 如果A≠B，则A+B=C与B+A=C视为不同的等式（A、B、C>=0） 3. n根火柴棍必须全部用上输入输入文件matches.in共一行，又一个整数n

数据库查询优化：利用范围查询和多值比较的等式区间优化技术

数据库查询优化：利用范围查询和多值比较的等式区间优化技术范围查询方法是数据库查询优化的一种重要手段，它通过利用索引来减少需要检查的数据行数，从而提高查询的执行效率。多值比较的等式区间优化当col_name列通过IN()操作符或者等价的OR条件与多个值进行比较时，这些比较被视为等值范围比较。这里的“范围”实际上指的是单个值的集合。优化器会估算满足这些等值范围比较的行数。如何估算行数

B3853：等式判断 ← 选择结构

【题目来源】https://www.luogu.com.cn/problem/B3853【题目描述】给出三个整数 a,b,c，保证 b≠0。如果a+b=c，请你输出 plus。如果a−b=c，请你输出 minus。如果以上两条均不满足，请输出 illegal。【输入格式】输入只有一行三个整数，依次表示 a,b,c。【输出格式】输出一行一个字符串表示答案。【输入样例】 1 2 3 3 2

火柴棍等式c语言

分析：我们可以枚举等式，在判断这些等式是由多少根火柴组成，在把火柴数量和之前输入的比较，如果相等，那么就统计一次，注意的是等号和加号需要减去四根。 #include <stdio.h>int f(int a){//判断某一个数字是由几根火柴组成的 int num[10]={6,2,5,5,4,5,6,3,7,6};int sum=0;if(a!=0){while(a){sum+=num[a

C语言代码之Harris-Benedict等式问题

代码： #include<stdio.h>int main(){double height,weight,BMR;int age;char s;double k;scanf("%lf %lf %d %c",&height,&weight,&age,&s);if(s=='F')BMR=655+(4.3*weight*2.2)+(4.7*height*0.39)-(4.7*age);el

matlab 等式化简,Matlab化简表达式多项式的操作步骤

亲们想知道Matlab化简表达式多项式的操作吗?下面就是小编整理的Matlab化简表达式多项式的操作步骤，赶紧来看看吧，希望能帮助到大家哦! Matlab化简表达式多项式的操作步骤相关指令简介这儿介绍下采用公因子发简化表达式的相关置换指令。气质要的函数指令为:“subexpr”。subexpr是替换表达式命令。在很多特繁琐的解析表达式中，常有个在不同地方重复出现的表达式，此时用sim

LaTex 数学公式：单个编号连等式

单个编号连等式的 LaTeX 写法如下： %%%%%% Equations %%%%%%\begin{align}L & = (a + b)^2 \nonumber \\& = a^2 + 2ab + b^2 \end{align} LaTex渲染结果如下： L = ( a + b ) 2 = a 2 + 2 a b + b 2 \begin{align} L &= (a +

C++编程解析-P1149火柴棒等式-函数

解题思路：首先，我们要将数字0-9所用的火柴棒数目存储到数组中，因为，n的范围小于等于24，所以，999是等式当中可能出现的最大的数字，所以，我们从0-999，挑选两个加数，计算出两个加数所用的火柴数目，再计算出两个加数和的火柴数目，将前两项火柴数目的和加上加号和等号所用的火柴数目。是否将火柴全部用完。用完则满足条件，否则，则不是。参考程序： #include<iostream>u

展开一个结构加法等式

4a6 4a8 - - - - - 1 - 1 - - - 1 - 1 - + - 1 - - 1 - - 1 - - 1 - - - - 在5-1的方向上具体展开4a6+4a8 25 19 19 19 19 19 19 19 25 19 19 19 19 19 19 19 1 10 10