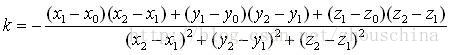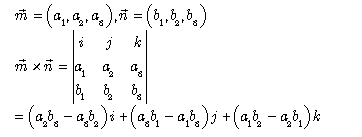点到专题
MATLAB 快速计算点到二维直线的距离并可视化(79)
计算点到二维直线距离,主要是还提供了具体的可视化方法 MATLAB 快速计算点到二维直线的距离并可视化(79) 一、算法介绍二、算法实现1.代码2.效果 一、算法介绍 问题:给定一条直线的方程 (Ax + By + C = 0) 和一个点 ((x_0, y_0)),点到直线的距离 (d) 方法:运行此脚本后,您将在 MATLAB 中看到一条红色的直线(倾斜 45
点到直线垂足计算公式Java实现
https://blog.csdn.net/jjwwwww/article/details/83830981转载 方便使用,自己记录一下! 求点到直线垂足 private Point getFoot(Point p1,Point p2,Point p3){Point foot=new Point();float dx=p1.x-p2.x;float dy=p1.y-p2.y;float u=
点到另外两点连线的垂足计算
假设空间某点O的坐标为(Xo,Yo,Zo),空间某条直线上两点A和B的坐标为:(X1,Y1,Z1),(X2,Y2,Z2),设点O在直线AB上的垂足为点N,坐标为(Xn,Yn,Zn)。点N坐标解算过程如下: 首先求出下列向量: 由向量垂直关系: 上式记为(1)式。 点N在直线AB上,根据向量共线: (2) 由(2)得: (3) 把(3)式代入(1)式,式中只
点到线段的最短矩离 及垂足的计算
过P做MN的垂线,垂足为Q,若Q在线段MN以内(包括与点M点N重合),则最短距离为垂线段长度,若垂足在MN以外,则最短距离为PM,PN中的较小者。(若P与MN共线,垂线长度为零,同样适用) 所以可由 Q位置判断 若Q在线段MN上 则 ∣ M Q ∣ 2 + ∣ Q N ∣ 2 ≤ ∣ M N ∣ 2 \lvert MQ \rvert ^2 + |QN|^2 \leq |MN|^2 ∣MQ∣2+
推导点到直线(平面)的距离公式
本文利用了点和直线、平面的齐次坐标表示方法,来推导2维点到直线距离,3维点到平面距离的公式。用齐次坐标表示方法推导比较简洁。 2维点到直线 令2维点: A ( x 0 , y 0 , 1 ) (x_0,y_0, 1) (x0,y0,1), 2维直线方程: a x + b y + c = 0 ax+by+c=0 ax+by+c=0 2维直线 ( a , b , c ) (a,b,c) (a
PCL 点到圆柱的距离(3D)
文章目录 一、简介二、实现代码三、实现效果参考资料 一、简介 这里的思路也很简单,我们只需要将点转换到圆柱坐标系下,在该系统中,点(0,0,0)为圆柱轴原点,(0,0,1)为圆柱轴方向,那么此时计算点到圆柱的距离就简单很多了,我们可以利用正射投影快速的获得距离结果。 二、实现代码 Cylinder3.h #pragma once#include "Line.h"
一个人的命运决定于晚上8点到10点之间
经典语录1:哈佛有一个著名的理论:人的差别在于业余时间,而一个人的命运决定于晚上8点到10点之间。每晚抽出2个小时的时间用来阅读、进修、思考或参加有意的演讲、讨论,你会发现,你的人生正在发生改变,坚持数年之后,成功会向你招手。不要每天抱着QQ/MSN/游戏/电影/肥皂剧……奋斗到12点都舍不得休息,看就看一些励志的影视或者文章,不要当作消遣;学会思考人生,学会感悟人生,慢慢的,你的人生将会发生变化
C++ 根据公式计算椭圆任意点到中心的距离
#include <iostream>using namespace std;double fact(int x) //定义阶乘函数。注意是double类型{double y = x; //注意是double类型for (int i = x-1; i > 0; i--)y *= i;return y;};double My_sin(int x) //定义sin函数。注意是double类型
空间点到平面的垂足坐标的计算方法以及matlab实现
问题描述: 已知空间点坐标(x,y,z),并且知道三个点的坐标(不要共线!),求解空间点到平面投影坐标。 参考百度文库的这篇文章 空间点到平面的垂足坐标的计算方法 下面是matlab的代码: %% 变量定义% 空间坐标点 x/y/z坐标分别为x4 y4 z4(需要手动修改!!)Data_Origin=[x4,y4,z4];% 取平面上的三个点 (不要共线!)% PlanePo
样本点到SVM超平面的距离
计算超平面系数 estimator_svm = svm.SVC(kernel="linear", C=1, gamma=1)#创建SVM模型estimator_svm.fit(x_train, y_train)#训练模型svm_predict = estimator_svm.predict
MySQL解决 恢复从备份点到灾难点之间数据(不收藏找不到了)
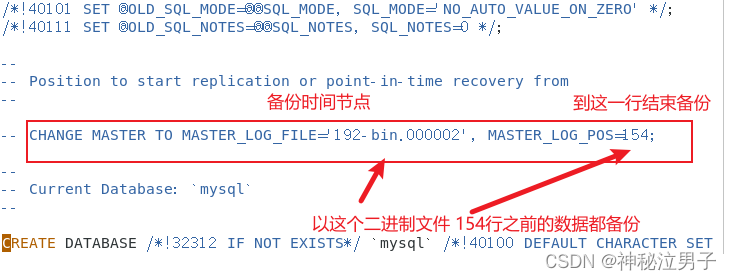
CSDN 成就一亿技术人! 今天分享一期 mysql中 备份之后发生灾难造成数据丢失 那么如何恢复中间的数据呢? 数据库数据高于一切(任何数据是不能丢失的) CSDN 成就一亿技术人! 目录 1.准备测试数据库 2.备份数据库 观察备份细节 3.(模拟备份点到灾难点的数据) 4.恢复测试 1.拷贝所有二进制文件 2.停止数据库 3.清理环境(模拟丢失) 4.还原备份前
MySQL解决 恢复从备份点到灾难点之间数据恢复
CSDN 成就一亿技术人! 今天分享一期 mysql中 备份之后发生灾难造成数据丢失 那么如何恢复中间的数据呢? 数据库数据高于一切(任何数据是不能丢失的) CSDN 成就一亿技术人! 目录 1.准备测试数据库 2.备份数据库 观察备份细节 3.(模拟备份点到灾难点的数据) 4.恢复测试 1.拷贝所有二进制文件 2.停止数据库 3.清理环境(模拟丢失) 4.还原备份前
圆拟合 --- 点到圆距离绝对值之和最小
https://www.researchgate.net/publication/220146330_Robust_Fitting_of_Circle_Arcs 根据这篇文章介绍的算法进行了实现,经过验证结果与论文中结果一致 AGE.h #pragma once#include <vector>struct Point2d {double x;double z;};struct Circl
1.ORB-SLAM3中如何保存多地图、关键帧、地图点到二进制文件中
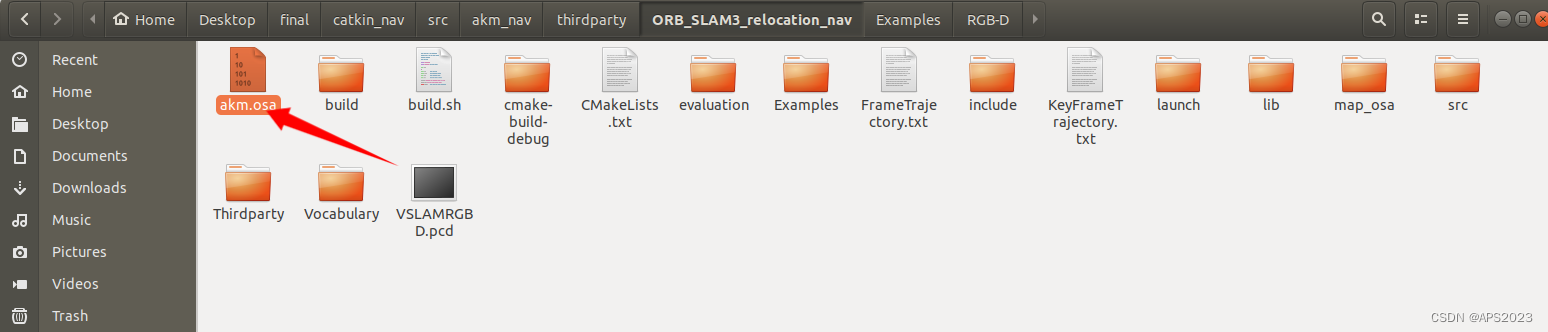
1 保存多地图 1.1 为什么保存(视觉)地图 因为我们要去做导航,导航需要先验地图。因此需要保存地图供导航使用,下面来为大家讲解如何保存多地图。 1.2 保存多地图的主函数SaveAtlas 2051 mStrSaveAtlasToFile是配置文件中传递的参数: 这里我们赋值成了akm(string mStrSaveAtlasT
点到线段所在直线的垂足
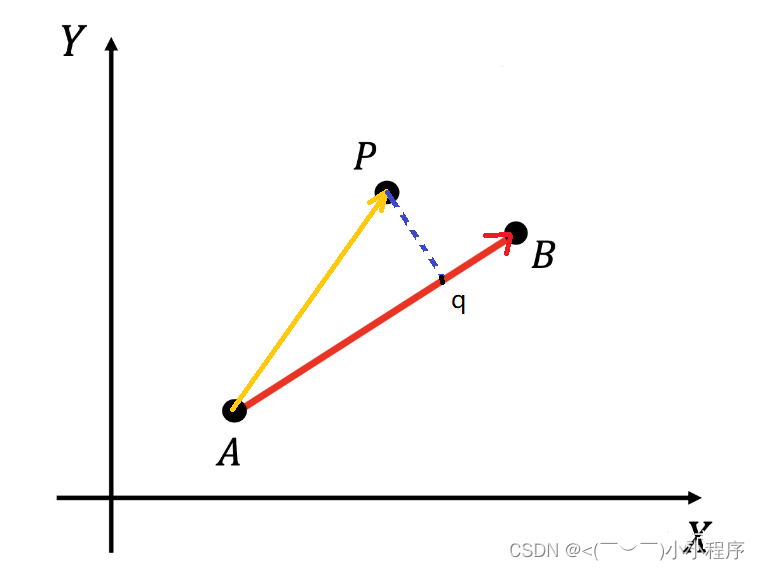
p点在现在AB上的垂足,就是AP在AB上的投影点,可以使用点乘计算。 点乘公式:a * b = |a||b|cosQ , 这个可以看成是投影关系表达式:cosQ = a * b / ( |a||b|); cosQ就是比例值,p点是投影在AB哪处。 double dotmultiply(POINT p1,POINT p2,POINT p0) { return ((p1.x-p0.x)*(p2.
点到直线垂足坐标c语言,平面坐标里计算点到线段的垂足问题
如图,以左上为原点的坐标图,坐标都为正 已知任意直线的点A,B, 和直线外一点C 目前用向量法还是直线方程的方法,然后都有偏移的情况 。 向量法结果在A点,直线方程结果在CB线上。 (另外线AB方向是不确定的,可能是AB也可能是BA, 可能是各种方向上) 现在的方法有时是正常的,有时是错误的, 图上是错误时的用例 向量法// 求垂足座标, C(x0,y0), A(x1, y1) B(x2, y
使用C++或者js求空间点到直线垂足坐标的解算方法
原文章地址为:https://blog.csdn.net/zhouschina/article/details/14647587 假设空间某点O的坐标为(Xo,Yo,Zo),空间某条直线上两点A和B的坐标为:(X1,Y1,Z1),(X2,Y2,Z2),设点O在直线AB上的垂足为点N,坐标为(Xn,Yn,Zn)。点N坐标解算过程如下: 首先求出下列向量: 由向量垂直关系,两个向量如果垂直,那么两
to_char用法:数据库跨时间段检索——几点到几点之间的数据,不管日期,比如说1月份每天下午2点到3点
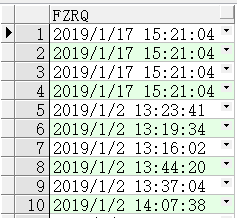
oracle数据库中,使用plsql执行查询,默认查询时间区间的语句为: select fzrq from dj_djb where FZRQ >= TO_DATE('2019-01-01 00:00:00','YYYY-MM-DD hh24:mi:ss') AND FZRQ <= TO_DATE('2019-02-28 23:59:59','YYYY-MM-DD hh24:mi:ss') 执
CSU 1503 点到圆弧的距离(最易理解)
第一步找出圆心 根据题目给出的三点建立两条直线,两直线垂直平分线的交点就是圆心 第二步判断点与圆弧的位置关系 通过分析,可分为两种情况; 情况一,ans1为p到p1的距离减去圆的半径的绝对值 情况二,ans2为p到A,C两点的距离最小值 给出f1,f2,f3,f4分别表示向量 p1A, p1B,p1C,p1P与x正半轴的夹角; 考虑到没有给出给点的顺序,有可能顺时针或逆时针给点。
Java 经纬度 距离 点到线 方位角
Java 中的经纬度(球体)的距离换算,两坐标点之间距离换算采用的为下面代码。和一些其他方法比较起来比较精确,因为网上所有的经纬度距离换算都不一样,但都能和主流的算法在几千KM的距离上只有几百米的差距。而且很大一部分差距来源于对地球半径的不统一。 距离 第一种 采用的为立体几何的弦之间的计算都是属于高中立体几何。画图比较容易计算出来 //地球半径public class Point {//
Java 实现判断时间是否在某个区间内(如是否在23点到凌晨4点之间)
最近遇到一个需求,就是判断一个时间是否在23点到凌晨4点之间,这个时间段是可以修改的。在网上收了一下发现没有符合我的需求的,就自己琢磨了一下,感觉这样算还是可以的。 思路: 如上图的那个圆形的钟表,可以从开始时间剪断,把钟表的环铺平,此时就变成了一个刻度尺,这样就好比较了 代码块 测试代码: public static void main(String[] args) {int s
敏捷团建游戏:从A点到B点的路
基本要求 分团队竞赛,每组5~9人每个团队从A点移动到B点(从教室或操场的一边到另一边),每人需采用不同动作姿势(如走、跑、爬、跳、背、抱、边唱边跳),用时短的团队赢三个迭代,三局两胜,同一团队每局都不能出现重复动作姿势 每迭代流程 三分钟计划会执行三分钟回顾会 特别规则 团队在移动过程中如出现卡壳(摔倒、不能保持动作或停顿超过3秒等),每出现一次,队长需脱掉一件衣服 最后每人分享OR
GIS技巧100例——14ArcGIS 点到线的最近垂线
这次GIS思维——GIS技巧100例的第十四讲《14ArcGIS 点到线的最近垂线 》 主要要实现点到一直线的最近的距离,以及最近点所在的位置,以及生成这一条垂线。 技术流程 下面直接视频教学吧 GIS技巧100例-GIS思维(持续更新中···) 推荐学习: ArcGIS之模型构建器(ModelBuild