点到另外两点连线的垂足计算

本文主要是介绍点到另外两点连线的垂足计算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

假设空间某点O的坐标为（Xo，Yo，Zo）,空间某条直线上两点A和B的坐标为：(X1,Y1,Z1),(X2，Y2，Z2),设点O在直线AB上的垂足为点N，坐标为(Xn，Yn，Zn)。点N坐标解算过程如下：

首先求出下列向量：

由向量垂直关系：

上式记为（1）式。

   点N在直线AB上，根据向量共线：

 （2）

  由（2）得：

（3）

   把（3）式代入（1）式，式中只有一个未知数k，整理化简解出k：

(4)
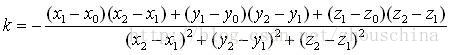
   把（4）式代入（3）式即得到垂足N的坐标。

C代码实现

// 二维空间点到直线的垂足
struct Point
{double x,y;
}
Point GetFootOfPerpendicular(const Point &pt,     // 直线外一点const Point &begin,  // 直线开始点const Point &end)   // 直线结束点
{Point retVal;double dx = begin.x - end.x;double dy = begin.y - end.y;if(abs(dx) < 0.00000001 && abs(dy) < 0.00000001 ){retVal = begin;return retVal;}double u = (pt.x - begin.x)*(begin.x - end.x) +(pt.y - begin.y)*(begin.y - end.y);u = u/((dx*dx)+(dy*dy));retVal.x = begin.x + u*dx;retVal.y = begin.y + u*dy;return retVal;
}

// 三维空间点到直线的垂足
struct Point
{double x,y,z;
}
Point GetFootOfPerpendicular(const Point &pt,     // 直线外一点const Point &begin,  // 直线开始点const Point &end)   // 直线结束点
{Point retVal;double dx = begin.x - end.x;double dy = begin.y - end.y;double dz = begin.z - end.z;if(abs(dx) < 0.00000001 && abs(dy) < 0.00000001 && abs(dz) < 0.00000001 ){retVal = begin;return retVal;}double u = (pt.x - begin.x)*(begin.x - end.x) +(pt.y - begin.y)*(begin.y - end.y) + (pt.z - begin.z)*(begin.z - end.z);u = u/((dx*dx)+(dy*dy)+(dz*dz));retVal.x = begin.x + u*dx;retVal.y = begin.y + u*dy;retVal.y = begin.z + u*dz;return retVal;
}

下面是我用java写的代码，就是翻译一下，也贴上：

   //点到其他两点垂足计算public TPoint getFoot(TPoint pt,TPoint beginPt,TPoint endPt){TPoint result = new TPoint();double dx = beginPt.getJd()-endPt.getJd();double dy = beginPt.getWd()-endPt.getWd();if(abs(dx)<0.000001&&abs(dy)<0.000001){result = pt;}double u = (pt.getJd()-beginPt.getJd())*(beginPt.getJd()-endPt.getJd())+(pt.getWd()-beginPt.getWd())*(beginPt.getWd()-endPt.getWd());u = u /(dx*dx+dy*dy);result.setJd(beginPt.getJd()+u*dx);result.setWd(beginPt.getWd()+u*dy);return result;}

 

这篇关于点到另外两点连线的垂足计算的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---