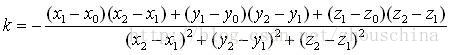垂足专题
点到直线垂足计算公式Java实现
https://blog.csdn.net/jjwwwww/article/details/83830981转载 方便使用,自己记录一下! 求点到直线垂足 private Point getFoot(Point p1,Point p2,Point p3){Point foot=new Point();float dx=p1.x-p2.x;float dy=p1.y-p2.y;float u=
点到另外两点连线的垂足计算
假设空间某点O的坐标为(Xo,Yo,Zo),空间某条直线上两点A和B的坐标为:(X1,Y1,Z1),(X2,Y2,Z2),设点O在直线AB上的垂足为点N,坐标为(Xn,Yn,Zn)。点N坐标解算过程如下: 首先求出下列向量: 由向量垂直关系: 上式记为(1)式。 点N在直线AB上,根据向量共线: (2) 由(2)得: (3) 把(3)式代入(1)式,式中只
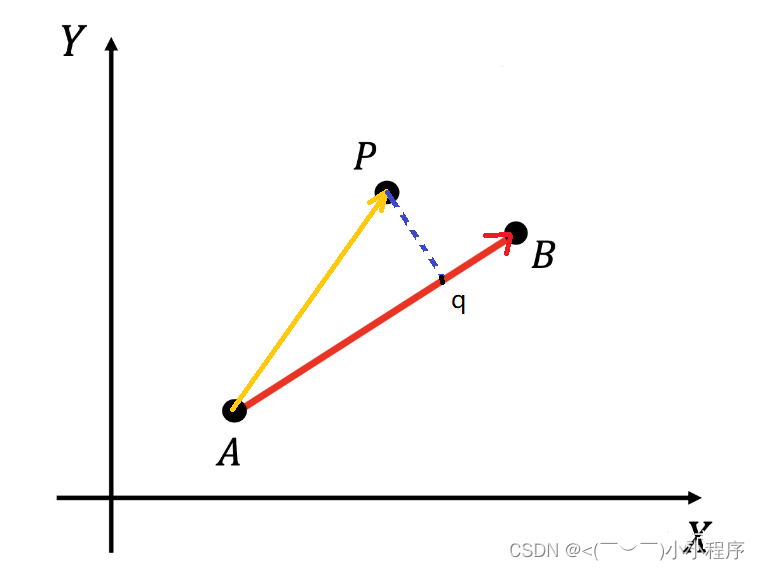
点到线段的最短矩离 及垂足的计算
过P做MN的垂线,垂足为Q,若Q在线段MN以内(包括与点M点N重合),则最短距离为垂线段长度,若垂足在MN以外,则最短距离为PM,PN中的较小者。(若P与MN共线,垂线长度为零,同样适用) 所以可由 Q位置判断 若Q在线段MN上 则 ∣ M Q ∣ 2 + ∣ Q N ∣ 2 ≤ ∣ M N ∣ 2 \lvert MQ \rvert ^2 + |QN|^2 \leq |MN|^2 ∣MQ∣2+
求一点在空间平面上的垂足
空间平面方程: Ax+By+Cz+D=0; 已知平面外待求垂足的空间点为P(x1,y1,z1); 已知该平面上一点:Pa(x0,y0,z0); 设垂足为Px; 设平面法向量:n(A,B,C) 则垂足为:Px=P-n/|n|●N/|n|●(P-Pa); 设n对应的单位法向量为nF; nF=n/|n| 则垂足为:Px=P-nF●nF●(P-Pa);
空间点到平面的垂足坐标的计算方法以及matlab实现
问题描述: 已知空间点坐标(x,y,z),并且知道三个点的坐标(不要共线!),求解空间点到平面投影坐标。 参考百度文库的这篇文章 空间点到平面的垂足坐标的计算方法 下面是matlab的代码: %% 变量定义% 空间坐标点 x/y/z坐标分别为x4 y4 z4(需要手动修改!!)Data_Origin=[x4,y4,z4];% 取平面上的三个点 (不要共线!)% PlanePo
点到线段所在直线的垂足
p点在现在AB上的垂足,就是AP在AB上的投影点,可以使用点乘计算。 点乘公式:a * b = |a||b|cosQ , 这个可以看成是投影关系表达式:cosQ = a * b / ( |a||b|); cosQ就是比例值,p点是投影在AB哪处。 double dotmultiply(POINT p1,POINT p2,POINT p0) { return ((p1.x-p0.x)*(p2.
点到直线垂足坐标c语言,平面坐标里计算点到线段的垂足问题
如图,以左上为原点的坐标图,坐标都为正 已知任意直线的点A,B, 和直线外一点C 目前用向量法还是直线方程的方法,然后都有偏移的情况 。 向量法结果在A点,直线方程结果在CB线上。 (另外线AB方向是不确定的,可能是AB也可能是BA, 可能是各种方向上) 现在的方法有时是正常的,有时是错误的, 图上是错误时的用例 向量法// 求垂足座标, C(x0,y0), A(x1, y1) B(x2, y
使用C++或者js求空间点到直线垂足坐标的解算方法
原文章地址为:https://blog.csdn.net/zhouschina/article/details/14647587 假设空间某点O的坐标为(Xo,Yo,Zo),空间某条直线上两点A和B的坐标为:(X1,Y1,Z1),(X2,Y2,Z2),设点O在直线AB上的垂足为点N,坐标为(Xn,Yn,Zn)。点N坐标解算过程如下: 首先求出下列向量: 由向量垂直关系,两个向量如果垂直,那么两