点到线段所在直线的垂足

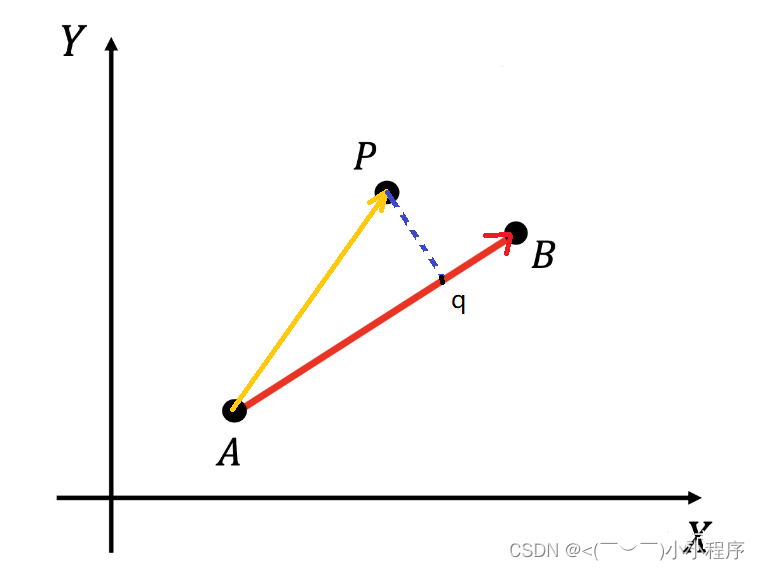
p点在现在AB上的垂足，就是AP在AB上的投影点，可以使用点乘计算。
点乘公式：a * b = |a||b|cosQ ，
这个可以看成是投影关系表达式：cosQ = a * b / ( |a||b|)；
cosQ就是比例值，p点是投影在AB哪处。

double dotmultiply(POINT p1,POINT p2,POINT p0) 
{ return ((p1.x-p0.x)*(p2.x-p0.x)+(p1.y-p0.y)*(p2.y-p0.y)); 
} 
double relation(POINT p,LINESEG l) 
{ LINESEG tl; tl.s=l.s; tl.e=p; return dotmultiply(tl.e,l.e,l.s)/(dist(l.s,l.e)*dist(l.s,l.e)); 
}
// 求点C到线段AB所在直线的垂足 P 
POINT perpendicular(POINT p,LINESEG l) 
{ double r=relation(p,l); POINT tp; tp.x=l.s.x+r*(l.e.x-l.s.x); tp.y=l.s.y+r*(l.e.y-l.s.y); return tp; 
}