Java 经纬度 距离 点到线 方位角

Java 中的经纬度（球体）的距离换算，两坐标点之间距离换算采用的为下面代码。和一些其他方法比较起来比较精确，因为网上所有的经纬度距离换算都不一样，但都能和主流的算法在几千KM的距离上只有几百米的差距。而且很大一部分差距来源于对地球半径的不统一。

距离

第一种
采用的为立体几何的弦之间的计算都是属于高中立体几何。画图比较容易计算出来

//地球半径
public class Point {//经度private double longtitude;//纬度private double latitude；
}//地球半径private static double EARTH_RADIUS = 6378.137;public static double DistanceOfTwoPoint(Point from,Point to){double radLat1 = from.getLatitude() * Math.PI / 180.0;double radLat2 = to.getLatitude() * Math.PI / 180.0;double a = radLat1 - radLat2;double b = from.getLongtitude()* Math.PI / 180.0 - to.getLongtitude()* Math.PI / 180.0;double s = 2 * Math.asin(sqrt(Math.pow(Math.sin(a/2),2) +Math.cos(radLat1)*Math.cos(radLat2)*Math.pow(Math.sin(b/2),2)));s=EARTH_RADIUS*s*1000;return s;}

第二种
最暴力最简单的方法，通过立体坐标系进行计算也是最容易算出来的。那么第一步就是将经纬度转换为三维坐标。也是需要一些基础的数学功底，经纬度在各个方向轴的映射。

 //将经纬度转化为弧度public static double torad(double deg) { return deg/180*acos(-1); }public static double[] ChangeLonAndLaToXY(Point target){//转为为弧度double lat = torad(target.getLatitude());double lng = torad(target.getLongtitude());double[] w=new double[3];//将弧度转为在映射三维坐标的长度double x =cos(lat)*cos(lng);double  y = cos(lat)*sin(lng);double z = sin(lat);w[0]=x;w[1]=y;w[2]=z;return  w;}

通过上面的代码我们就可以将经纬度映射成一个在圆上的坐标。圆心即为地球地心，半径为1（为什么选1呐不再乘地球半径呐，因为后面我们只需要弧长即只需要向量角度，而模长均为1的向量在计算角度是只需要取向量乘积就可以得到cos，而且由于地球半径的长度，我们放在最后也能最好的保证我们计算中间更少的精度丢失。

）；
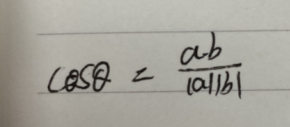
简单的数学问题两向量的三维坐标求夹角。

//计算两模为1的向量之间的cos夹角public static double CalculateAngle(double[] first,double[] second){double result=first[0]*second[0]+first[1]*second[1]+first[2]*second[2];return result;}

既然cos有了弧度也就出来了（为什么求弧度那，问这样问题的人 肯定没有自己想自己画图，这个我会放在最后面给你解答，而且也有对圆形几何的全面解答）

             //计算弧度double result1=Math.acos(result);//根据弧度求弧长System.out.println(result1*6378.137*1000);

我们来比较下1 2两种方法的差距

1824270.8541038772
1824270.4198887048

到了几乎没有差距的程度，很正常，因为计算中间精度的差距还是有点区别的。
解惑

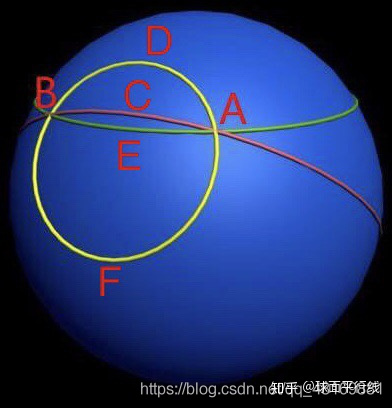
球上是没有看上去直直的直线的，只有曲面直线，而且我们说圆上两点可以有无数条曲面直线的。是不是很疑惑了那么我们求的是什么东西，这样问的人肯定没有自己思考。一般我们说球上两点的距离是以同时过圆心的那个大圆的弧长来说的（三点成一面），这个弧长也是所有过两点的圆的弧长的最短距离，即两点间的最短距离。所有我们求最短距离就求过圆心的弧长就行了。

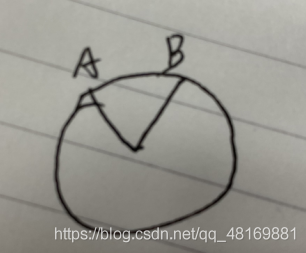
求出ab的夹角根据弧度转弧长就可得到ab在圆上的最短距离。如果不按弧度求按三角几何的话那就是ab的连线的直线距离了。你要穿地球吗?

点到线

以下代码为在地球球体上 两个坐标点为一条直线，另一个坐标点相对于这条线的最短距离。首先将情况分为两种
第一种
坐标点 经纬度差距很小的情况下，就可以近似的看成是平面图形 。求平面图形的点到线的距离是很简单的。已知三点经纬度 可以根据上面的方法算出三个点互相的距离 a b c，三个点互相连线为一个三角形。由三角形面积
p=（a +b+c）/2

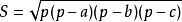
s=底*高/2 。高为点到线的最短距离 根据以上公式可求出最短距离

public static double DistanceOfPointToLine(Point lineone,Point linetwo,Point from){//求出三边长度double disLine=DistanceOfTwoPoint(lineone,linetwo) ;double disOne=DistanceOfTwoPoint(lineone,from);double disTwo=DistanceOfTwoPoint(linetwo,from);//判断是否在同一条线上，误差计算可能出现两条直线距离小于直线长度的情况if((disOne+disTwo)<=disLine) return 0;//求出三角形面积double p=(disLine+disOne+disTwo)/2;System.out.println(disLine);System.out.println(disOne);System.out.println(disTwo);System.out.println(p);double s=sqrt(p*(p-disLine)*(p-disOne)*(p-disTwo));//返回Line的高即为点到线距离return 2*s/disLine;}

第二种
在事实上地球为一个椭圆，所有如果在经纬度差距 范围够大的情况下，这种情况是不可能看成是平面图形的。这样将会造成很大误差。那么将地球看成一个椭圆或者球体那么不可避免的就要接触到球体几何。这时候我们就要换一种算法来计算了，虽然求点到点的距离用弦之间的转换挺容易但是我们点到线之间的转换就有点麻烦了，你可以自己去试一试，挺麻烦的。所以我们采用坐标系暴力解法。

首先对问题进行解读 点到线，即为点到另外两点和圆心组成的大圆（过圆心的圆切面）的最短距离。
点到圆上两点组成的圆切面的距离，就是我们在一个空间上点到平面的最短距离，只不过我们这个最短
距离不可能是直线因为我们不可能通过地球穿过去，所有我们只能也是过大圆的圆弧长度。如果你不理解我说的话，这些话的证实结果：两个相切的大圆求弧长。 我们只要求出这个角度就行。这个角度就是线和平面的夹角。我们知道这个平面中的两条向量 就是a b经纬度转换为的向量。 高中知识 线和一平面组成的夹角我们怎么求 求出它的法向量就行了，然后我们计算法向量和这条直线的cos 直角的一∠cos等于另一∠sin的那么我们就可以得出角度 即就可以求出弧度接下来就可以求出弧长。

求法向量方法很多矩阵解三元一次方程，还有高中学的公式，自己推也可以。

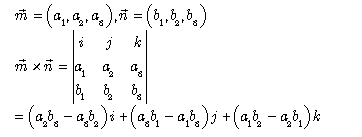
那么我们要求出法向量 然后把法向量的模转为1

//计算两向量的法向量public static double[] CalculateNormalVector(double[] first,double[] second){double[] result=new double[3];//根据矩阵公式算出模不为1的法向量double x=first[1]*second[2]-first[2]*second[1];double y=first[2]*second[0]-first[0]*second[2];double z=first[0]*second[1]-first[1]*second[0];//将法向量转为模为1的法向量result[0]=x;result[1]=y;result[2]=z;SloveUtils.ChangeDisModelTo1(result);return result;}//将向量转为模为1的向量方便用于夹角的计算public static void ChangeDisModelTo1(double [] target){//模长double disModel=Math.sqrt(target[0]*target[0]+target[1]*target[1]+target[2]*target[2]);target[0]=target[0]/disModel;target[1]=target[1]/disModel;target[2]=target[2]/disModel;}

之后求出法向量和那条直线的夹角还是我们前面封装过得夹角公式

 public static double CalculateAngle(double[] first,double[] second){double result=first[0]*second[0]+first[1]*second[1]+first[2]*second[2];return result;}

之后又是很简单的计算调用环节

  //点到线的比较精确距离public static double DistanceOfPointToLineAcc(Point lineone,Point linetwo,Point from){//将3个经纬度转为两条在三维坐标系模为1的向量double[] vectorone=SloveUtils.ChangeLonAndLaToXY(lineone);double[] vectortwo=SloveUtils.ChangeLonAndLaToXY(linetwo);double[] vectorfrom=SloveUtils.ChangeLonAndLaToXY(from);//计算出两向量的法向量double[] normalvector=SloveUtils.CalculateNormalVector(vectorone,vectortwo) ;//计算法向量和向量的cos值 即为from向量和其他两向量组成平面的夹角的sin值double cos=SloveUtils.CalculateAngle(normalvector,vectorfrom);//将cos转为弧度double result=Math.abs(Math.asin(cos));return  result*EARTH_RADIUS*1000;}

那么我们和第一种的比较看看差距有多大呐 几百km的时候差距还不是特别大，之后就会越来越大的。

1679767.499186938 1676185.9071493528

另外一种说明第一种有点不靠谱的方式：
那么还是按照平面几何来算的话大概会有多大的误差呐。我们可以采用极限的方法进行计算 a b c三点将 b c点的距离无限接近而且abc三角形为锐角三角形那么a在b c直线上的高即为a到b的距离亦或者a到c的距离。那么我们再次采用我们的两个坐标点的距离公式 a b点的距离方法。就可以得出点到直线的距离在大经纬度差距的情况下到底误差了多少。这里我将b c的纬度改变了0.00001（可忽略不计）

private static double rad(double d) {return d * Math.PI / 180.0;}public static void main(String[] args){Point a=new Point(1.6119,25.06306);Point c=new Point(121.6119,25.06306);Point b=new Point(121.6119,25.06305);//两点之间距离System.out.println(""+MapUtils.DistanceOfTwoPoint(a,b));//由平面几何高得出的两点之间的距离System.out.println(""+MapUtils.DistanceOfPointToLine(b,c,a));}

结果为：1.1504384710009279E7 9275466.80930289
由此看出误差达到了 %19 而且这个误差还将随着差距的扩大而扩大这是非常不可取的 这里我们选得经纬度差距比较大 所有看起来比较夸张，但是在一两千km距离时误差也挺小的%1都不到。

最后
另外提供方位角代码

方位角

 private  static double getAngle1(double lat_a, double lng_a, double lat_b, double lng_b) {double y = Math.sin(lng_b-lng_a) * Math.cos(lat_b);double x = Math.cos(lat_a)*Math.sin(lat_b) - Math.sin(lat_a)*Math.cos(lat_b)*Math.cos(lng_b-lng_a);double brng = Math.atan2(y, x);brng = Math.toDegrees(brng);if(brng < 0)brng = brng +360;return brng;}

（求大神指点）