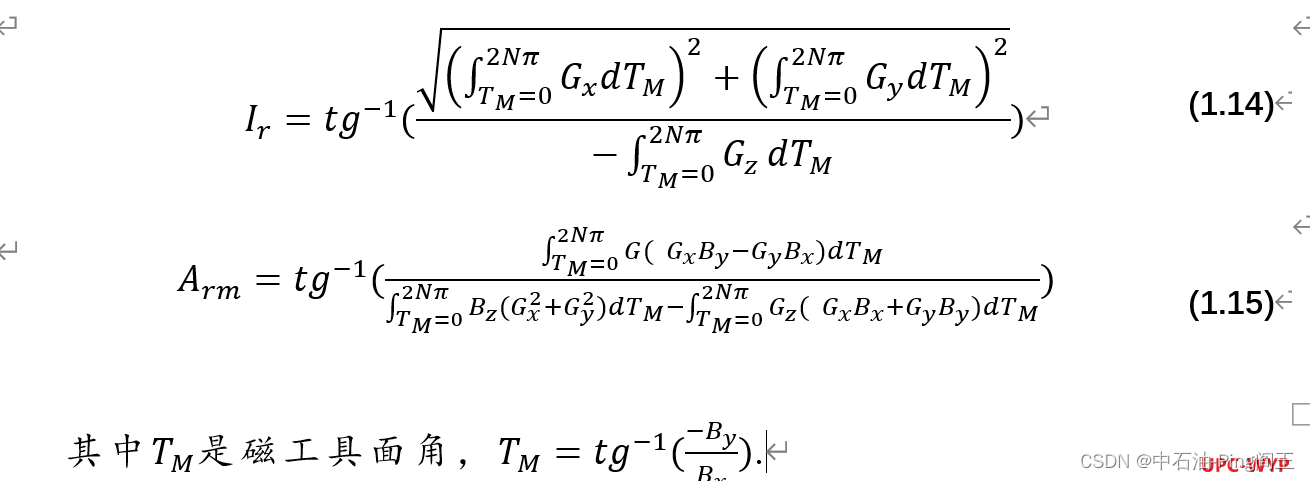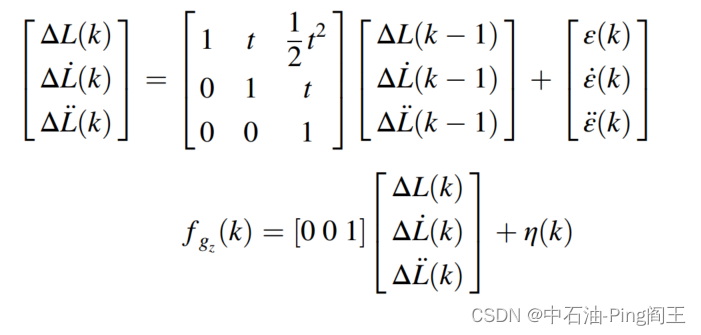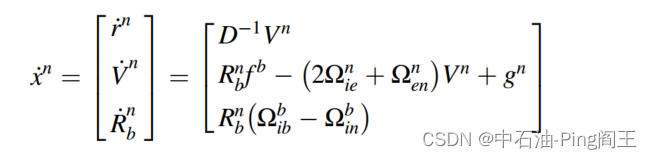方位角专题
计算两个经纬度点之间的方位角(初始方位角)
最近做地图上轨迹计算方位角的时候,需要计算两个经纬度点之间的方位角,这里把计算过程记录分享一下。 一:思路 要计算两个经纬度点之间的夹角(通常称为方位角或初始方位角),你可以使用大圆距离公式或者一些近似方法。 假设你有两个点,点A(纬度LatA, 经度LonA)和点B(纬度LatB, 经度LonB)。你可以使用以下公式来计算从点A到点B的方位角(以度为单位): 计算经纬度差值(以弧度为单位):
Android 卫星通信计算方位角,仰角,极化角
需求描述: 已知手机的经纬度和高度信息,需要通过公式计算出手机收星的最优方位和仰角,用以调整UI界面显示,以便引导用户实现和当前卫星方位和仰角的对准,达到快速入网的目的。 术语说明 术语说明方位角手机天线在所处位置针对北极的偏转角度,顺时针为正,逆时针为负仰角手机天线在所处位置针对地平面的仰角极化角天线馈源和电磁波的夹角,方位角和仰角的调节参数 /*** 计算卫星天线的方位角**
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
磁性测量工具安装在非磁性钻铤内,如图1,以避免磁性随钻测量工具测量时受到外部干扰。 测量系统采用三轴加速度计和三轴磁通门,并采用冗余设计,由于井下振动剧烈,陀螺仪的可靠性将大大降低。为了保证整个钻井过程中系统的可靠性,我们只以陀螺仪的测量信号作为参考。采用非磁性钻铤将电子测量仪器与上下钻柱的磁场分开,防止传感器处地球磁场的畸变。 当*钻柱旋转时,静态测量的公式不再适用 *。当传感器安装在旋转钻柱的
三轴地磁方位角原理及代码实现
开发平台:Arduino 控制板:Mbsbot-Mega2560版本 姿态传感器:GY85九轴模块 实现目标: 通过地磁计模块获取姿态角,位移量,估算当前相对位移 1.获取地磁计方位角 库函数获取地磁计原始数据 float* magScaled = sen10724.readMagScaled();max_x = max(magScaled[0], max_x);min_x =
Vue.js2+Cesium1.103.0 十五、计算方位角
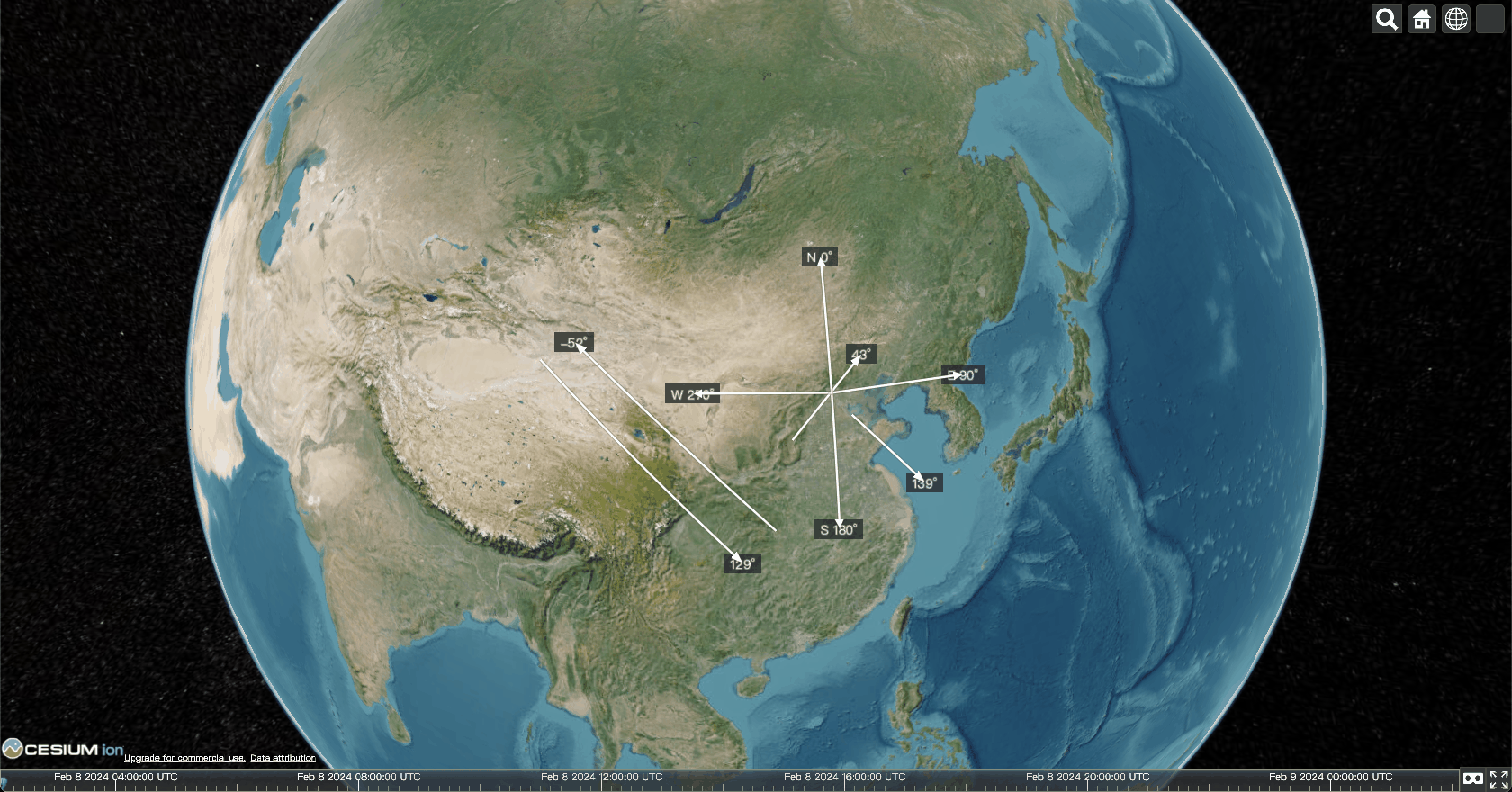
Vue.js2+Cesium1.103.0 十五、计算方位角 Demo <template><divid="cesium-container"style="width: 100%; height: 100%;"/></template><script>/* eslint-disable no-undef *//* eslint-disable new-cap *//* eslint
leaflet学习笔记-带有方位角信息的圆的绘制(七)
前言 项目中有一个需求,就是需要绘制一个圆,并且绘制的时候还要设置方位角,最后返回圆的坐标集合和方位角。本功能使用Leaflet-Geoman+Turf.js+leaflet实现。 方位角简介 在陆地导航中,方位角通常表示为 alpha、α,并定义为从北基线或子午线顺时针测量的水平角。方位角也被更广泛地定义为从任何固定参考平面或容易建立的基准方向线顺时针测量的水平角度。 今天,方位角的参考
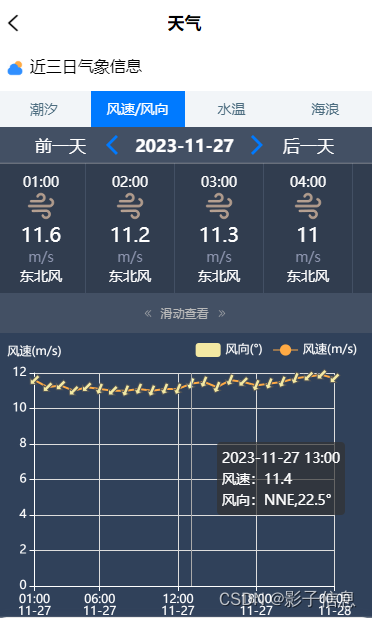
风向,NNE表示北西北,根据风向的定义,从方位角在337.5°±11.25°范围内吹来的风的风向都记为NNW。
理论: 在气象观测中,风向是指风的来向,地面风向用十六个方位表示,在气象服务过程中一般用汉语表述,在专业领域用英文字母表示,分别是:北(N)、东北东(NNE)、东北(NE)、东东北(ENE)、东(E)、东东南(ESE)、东南(SE)南东南(SSE)、南(S)、南西南(SSW)、西南(SW)、西西南(WSW)、西(W)、西西北(WNW)、西北(NW)、北西北(NNW)。根据风向的定义,从方位角
Java 经纬度 距离 点到线 方位角
Java 中的经纬度(球体)的距离换算,两坐标点之间距离换算采用的为下面代码。和一些其他方法比较起来比较精确,因为网上所有的经纬度距离换算都不一样,但都能和主流的算法在几千KM的距离上只有几百米的差距。而且很大一部分差距来源于对地球半径的不统一。 距离 第一种 采用的为立体几何的弦之间的计算都是属于高中立体几何。画图比较容易计算出来 //地球半径public class Point {//
太阳天顶角、方位角、高度角计算
1.利用python中库ephem实现计算 import ephem import datetime as datetime import math def calculate_solar_zenith_angle(latitude, longitude, elevation, date_time): # 创建观测者对象 observer = ephem
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
一、 卡尔曼滤波 卡尔曼滤波的应用要求系统和底层过程的测量模型都是线性的。离散时间线性状态空间系统的描述为: x k = Φ k , k − 1 x k − 1 + G k − 1 w k − 1 x_k=\Phi_{k,k-1}x_{k-1}+G_{k-1}w_{k-1} xk=Φk,k−1xk−1+Gk−1wk−1 式中 Φ k , k − 1 \Phi_{k,k-1}
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
一、内容介绍 该测量系统基于三轴加速度和三轴陀螺仪,安装在钻柱内部,随钻柱一起旋转,形成捷联惯性导航系统,安装如下图所示: 假设三轴加速度和陀螺仪的输出为: f b = [ f x f y f z ] T f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z} \end{bmatrix}^T fb=[fxfyfz]T w b = [ w x w y