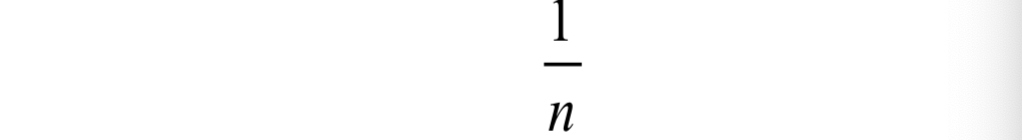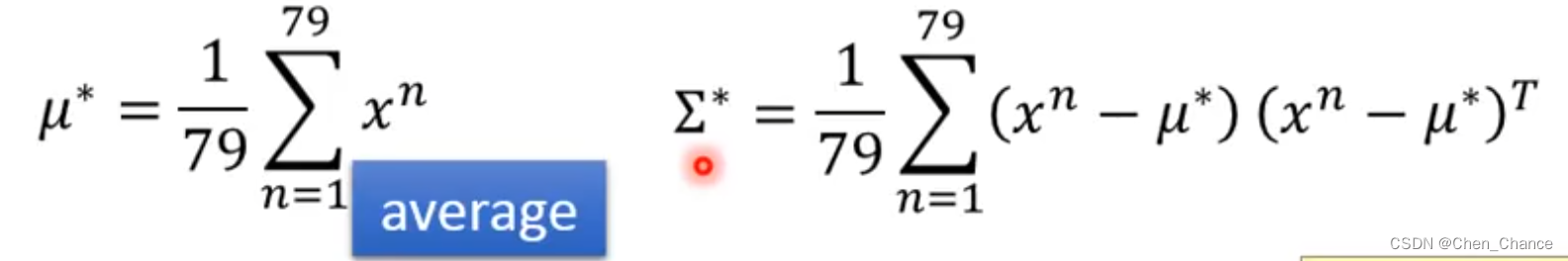概率密度函数专题
如何理解概率分布函数和概率密度函数?
我的理解: 当是离散型时,概率函数为pi=P(X=ai)(i=1,2,3,4,5,6),每次只能取一个点的概率;把所有可能的离散型随机变量的值分布和值的概率都列举出来那就是概率分布;概率分布函数就是在某一个区间内概率发生的情况,也就是概率函数取值的累加结果,例如F(X)=P(X<=a) =X取值小于等于a时的概率和。 当是连续性时,概率密度函数(对应于离散型的概率函数)有具体的意义,但是不能直接
引入分布函数和概率密度函数解释:三种常见连续型随机变量的分布(均匀、指数、正态)
连续性随机变量及其分布 在概率论和统计学中,我们常常会接触到连续性随机变量及其分布。连续性随机变量的一个显著特征是其取值可以在一个连续的范围内变化,比如温度、身高、体重等。为了更好地理解和分析这些随机变量,我们需要使用分布函数和概率密度函数。 分布函数和概率密度函数 **分布函数(Cumulative Distribution Function, CDF)**是描述一个随机变量取值小于或等于
概率密度函数、概率分布函数、概率质量函数
1.概率密度函数 1.1. 定义 如果对于随机变量X的分布函数F(x),存在非负函数f(x),使得对于任意实数有 则称X为连续型随机变量,其中F(x)称为X的概率密度函数,简称概率密度。(f(x)>=0,若f(x)在点x处连续则F(x)求导可得) f(x)并没有很特殊的意义,但是通过其值得相对大小得知,若f(x)越大,对于同样长度的区间,X落在这个区间的概率越大。
二元正态分布的概率密度函数
二元正态分布随机变量 如果随机变量 X X X、 Y Y Y的联合PDF为 p X , Y ( x , y ) = 1 2 π σ x σ Y 1 − p 2 exp { − ( x − μ X ) 2 σ X 2 + ( y − μ Y ) 2 σ Y 2 − 2 ρ ( x − μ X ) ( y − μ Y ) σ X σ Y 2 ( 1 − ρ 2 ) } p_{X,Y}(x,y
估计理论(2):多元高斯变量的条件概率密度函数(PDF)
本节内容摘自Steven M. Kay,《Fundamentals of Statistical Signal Processing: Estimation Theory》。 【定理10.2】多元高斯向量的条件PDF 如果 x ∈ R k × 1 {\bf x}\in \mathbb{R}^{k\times 1} x∈Rk×1和 y ∈ R l × 1 {\bf y}\in \mathbb{R
概率密度函数(PDF)与神经网络中的激活函数
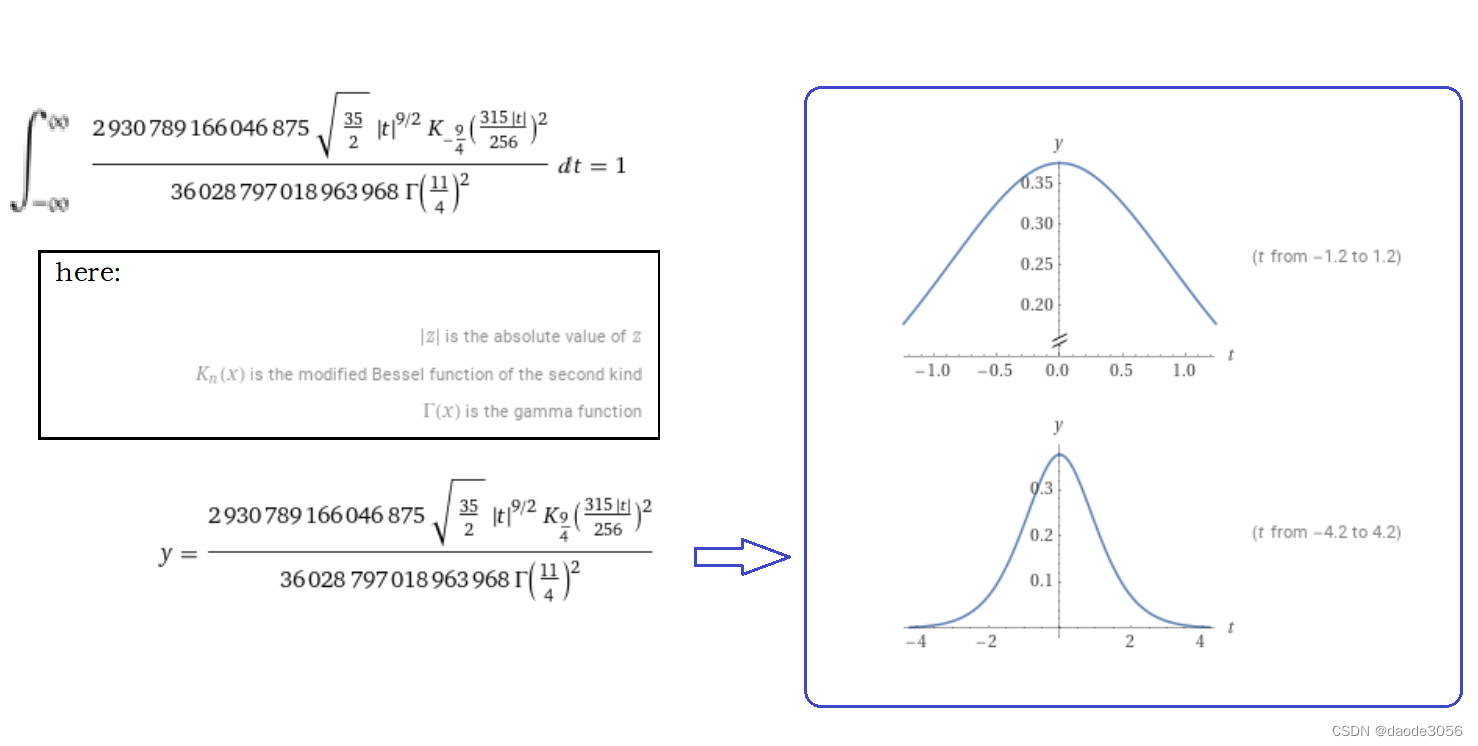
原创:项道德(daode3056,daode1212) 在量子力学中,许多现象都是统计的结果,基本上用的是正态分布,然而,从本质上思考,应该还存在低阶的分布,标准的正态分布是它的极限,这样一来,或许在某些状态,要多关注瞬间与低能的统计分布,这就要推出一些低阶的分布,些分布大多都要出现特殊函数,先看看Bessel function: 以下是作者应用“第二类虚宗量的贝塞尔函数”
概率密度函数(PDF)正态分布
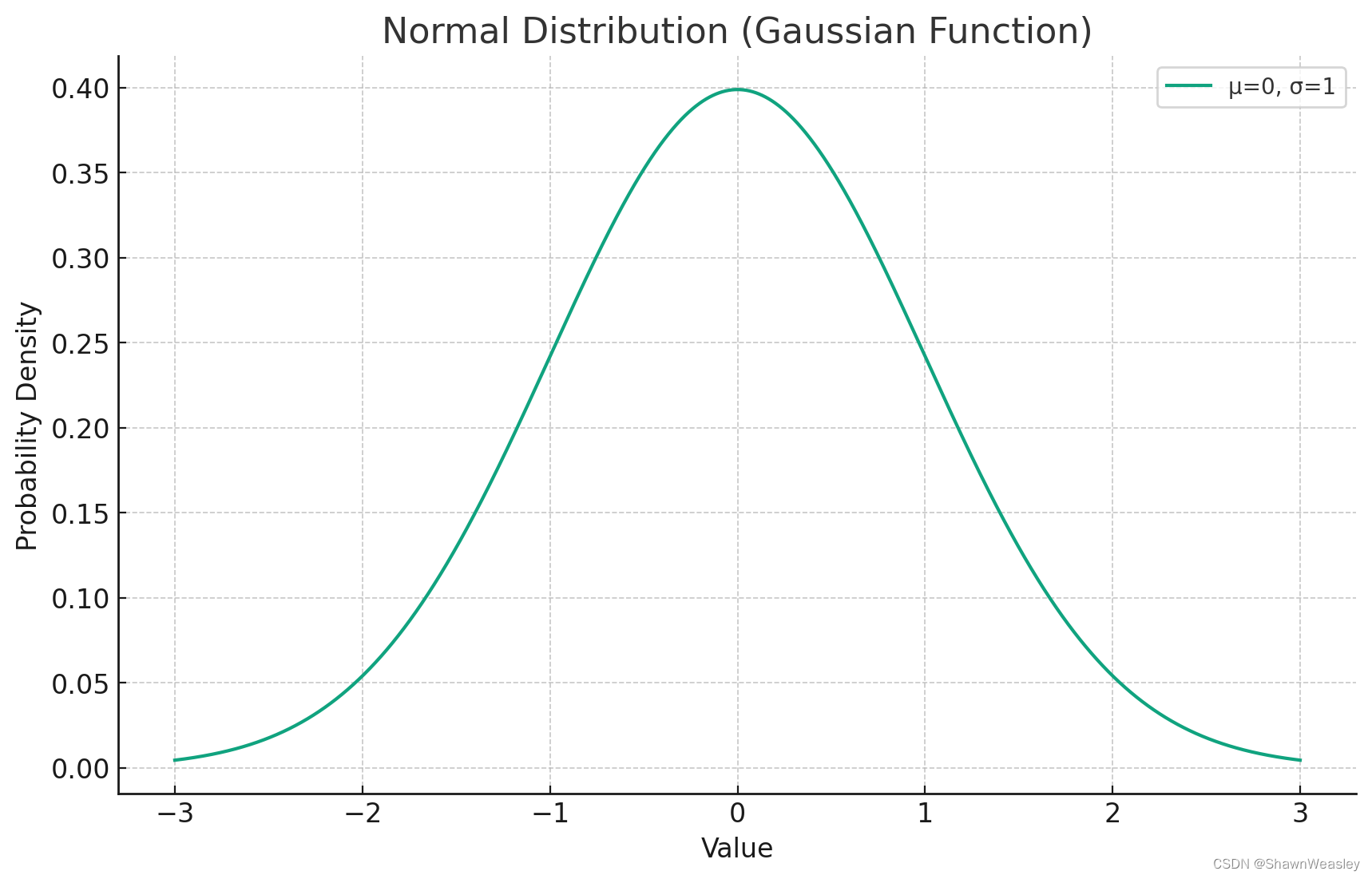
概率密度函数(PDF)是一个描述连续随机变量取特定值的相对可能性的函数。对于正态分布的情况,其PDF有一个特定的形式,这个形式中包括了一个常数乘以一个指数函数,它假设误差项服从均值为0的正态分布: p ( ϵ ( i ) ) = 1 2 π σ 2 exp ( − ( ϵ ( i ) ) 2 2 σ 2 ) p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi\s
累计概率分布、概率分布函数(概率质量函数、概率密度函数)、度量空间、负采样(Negative Sampling)
这里写自定义目录标题 机器学习的基础知识累计概率分布概率分布函数度量空间负采样(Negative Sampling)基于分布的负采样(Distribution-based Negative Sampling):基于近邻的负采样(Neighbor-based Negative Sampling): 机器学习的基础知识 累计概率分布、概率分布函数(概率质量函数、概率密度函数)、度
多维高斯分布(多元正态分布)的概率密度函数和最大似然估计
多元高斯分布的概率密度函数 f μ , Σ ( x ) = 1 ( 2 π ) D / 2 1 ∣ Σ ∣ 1 / 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } f_{\mu, \Sigma}(x)=\frac{1}{(2 \pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} exp\{-\frac{1}{2}(x-\mu)^T
多维高斯分布(多元正态分布)的概率密度函数和最大似然估计
多元高斯分布的概率密度函数 f μ , Σ ( x ) = 1 ( 2 π ) D / 2 1 ∣ Σ ∣ 1 / 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } f_{\mu, \Sigma}(x)=\frac{1}{(2 \pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} exp\{-\frac{1}{2}(x-\mu)^T
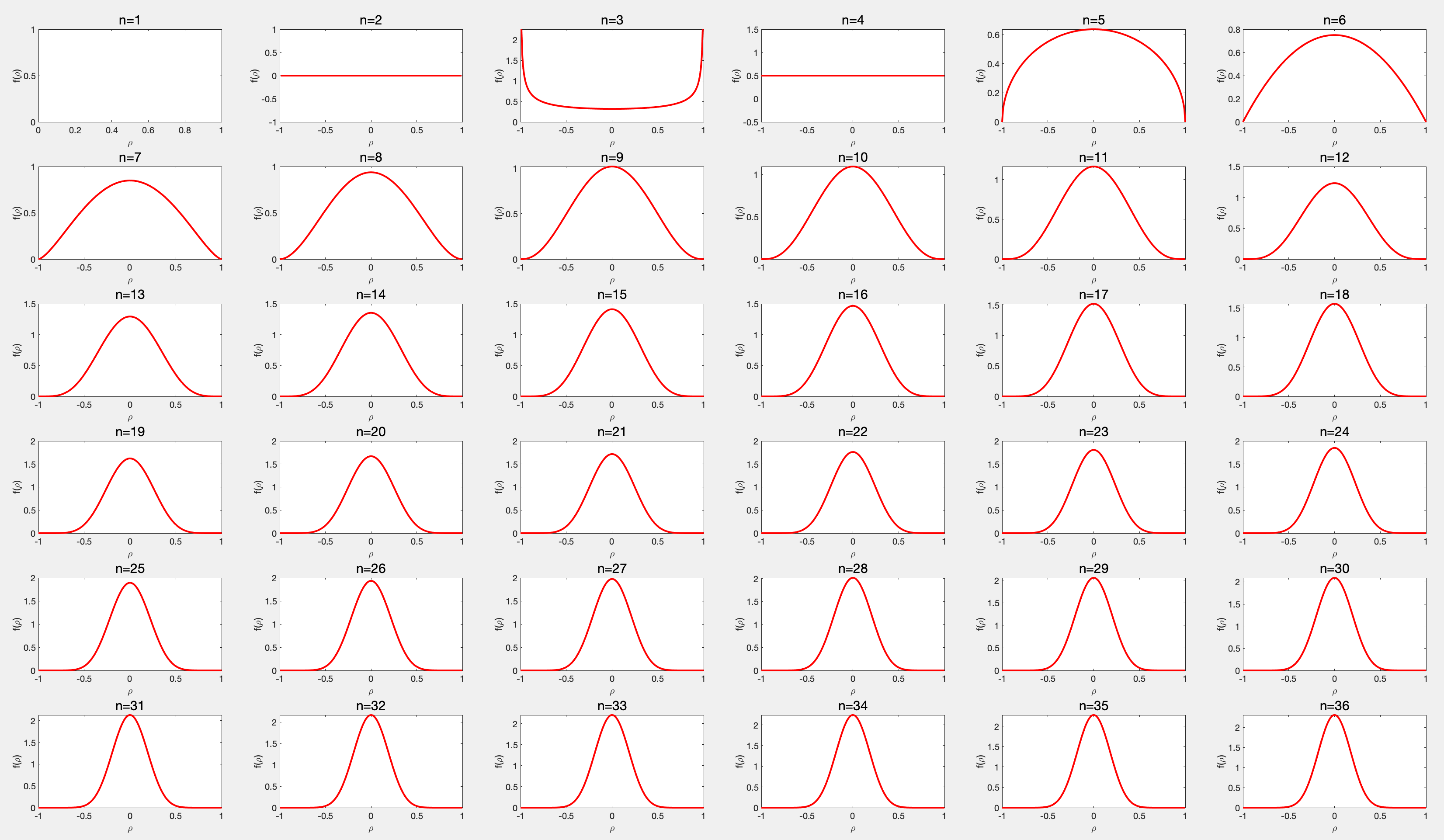
相关系数的概率密度函数分布
相关系数的概率密度函数分布 看了一圈相关系数假设检验的网页,大部分都是t检验z检验什么的,也就是通过构造 ρ \rho ρ的统计量进行假设检验,有一个大佬推导了更直接的样本相关系数的估计及其分布,然后我也在《高等测量平差》P33页看到了 在文献4中已导出在原假设成立( ρ = 0 \rho=0 ρ=0)时, ρ ^ \hat \rho ρ^的密度函数为 f ( ρ ^ ) = Γ ( n