最优专题
一些数学经验总结——关于将原一元二次函数增加一些限制条件后最优结果的对比(主要针对公平关切相关的建模)
1.没有分段的情况 原函数为一元二次凹函数(开口向下),如下: 因为要使得其存在正解,必须满足,那么。 上述函数的最优结果为:,。 对应的mathematica代码如下: Clear["Global`*"]f0[x_, a_, b_, c_, d_] := (a*x - b)*(d - c*x);(*(b c+a d)/(2 a c)*)Maximize[{f0[x, a, b,
4-4.Andorid Camera 之简化编码模板(获取摄像头 ID、选择最优预览尺寸)
一、Camera 简化思路 在 Camera 的开发中,其实我们通常只关注打开相机、图像预览和关闭相机,其他的步骤我们不应该花费太多的精力 为此,应该提供一个工具类,它有处理相机的一些基本工具方法,包括获取摄像头 ID、选择最优预览尺寸以及打印相机参数信息 二、Camera 工具类 CameraIdResult.java public class CameraIdResult {
华为OD机试 - 最优结果的a数组数量 - 贪心思维(Java 2024 E卷 100分)
华为OD机试 2024E卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(E卷+D卷+A卷+B卷+C卷)》。 刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,每一题都有详细的答题思路、详细的代码注释、3个测试用例、为什么这道题采用XX算法、XX算法的适用场景,发现新题目,随时更新,全天CSDN在线答疑。 一、题目描述
清华MEM作业-利用管理运筹学的分析工具slover求解最优解的实现 及 通过使用文件或者套节字来识别进程的fuser命令
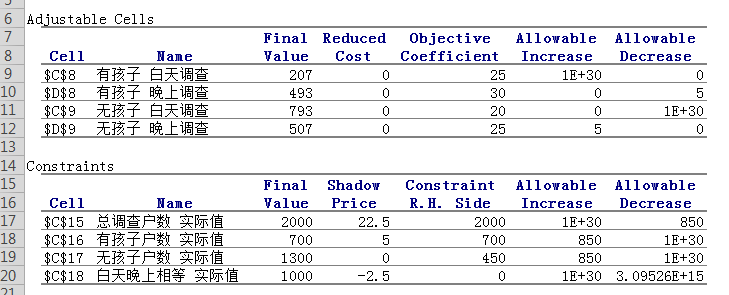
一、清华MEM作业-利用管理运筹学的分析工具slover求解最优解的实现 最近又接触了一些线性求解的问题,以前主要都是在高中数学里接触到,都是使用笔算,最后通过一些函数式得出最小或者最大值,最近的研究生学业上接触到了一个Excel solver分析工具,对这种线性求最优解的问题感觉使用起来真是得心应手。在使用这个工具前,EXCEL里需要先装上solver工具,装起来很也简单,网上
【POJ】2728 Desert King 最优比率生成树——01分数规划【经典】
最近在刷巨巨们放出来的专题,然后没做几题就卡住了,果然还是太弱了T U T... 这次做到了一题01分数规划求解的生成树问题。 题目大意是这样的:给你一个无向完全图,每条边i都有两个权值,长度a[ i ],花费b[ i ],需要选出其中的一些边构造一颗生成树,生成树需要满足条件:∑ b [ i ] / ∑ a [ i ]最小。 这样我还是先来介绍一下01分数规划吧~ 给定一个上述的问
2024国赛数学建模备赛|30种常用的算法模型之最优算法-非线性规划
1.1 非线性规划的实例与定义 如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问题。一般说来,解非线性规划要比解线性规划问题困难得多。而且,也不象线性规划有 单纯形法这一通用方法,非线性规划目前还没有适于各种问题的一般算法,各个方法都 有自己特定的适用范围。 下面通过实例归纳出非线性规划数学模型的一般形式,介绍有关非线性规划的基本 概念。 最佳投资方案应是投资
超好用的图纸加密软件排行榜 | 2024图纸加密软件的七款最优选择!
数字化设计日益普及的今天,图纸作为设计与工程的核心载体,其安全性成为了企业和设计师们最为关注的焦点之一。 面对日益复杂的数据泄露风险,如何有效地保护图纸文件的安全呢? 下面,我们就来探讨一下2024图纸加密软件的最优选择,为您介绍七款超好用的图纸加密软件! 一、域智盾:专业级图纸加密的领军者 ①透明加密 采用基于Windows文件系统驱动开发的透明加密技术,结合高强度国际流行加密算法
最短路径算法:迪杰克斯拉(Dijkstra)算法(基于贪心思想)【从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题】【能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低】
Dijkstra算法是典型最短路算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。 Viterbi和Dijkstra算法看起来比较像,两者的区别: Dijkstra算法适应范围更广。Viterbi算法用在特殊的有向无环图中,而Dijkstra算法可以用在
【Spfa】noip2009 最优贸易
最优贸易 (trade.pas/c/cpp) 【问题描述】 C 国有n 个大城市和 m 条道路,每条道路连接这n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为1 条。 C 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。但是,同
问题最优解:实际问题转换图论问题
文章目录 图论的本质概念理解指标衡量哪些实际问题可以转换成图论问题?案例:城市交通优化 图算法的作用及求解优化概念理解指标衡量案例:网络流量优化 图论的局限性与可能性概念理解指标衡量案例:社交网络中的用户行为分析 图论结构与模型概念理解指标衡量哪些场景问题可以转换成图模型?案例:医疗诊断中的贝叶斯网络 图论与机器学习概念理解指标衡量常见场景案例:社交网络中的用户行为预测 图算法的并行化与分布
HDU_1533 Going Home(最优匹配)
说实话,这个题目刚开始还真看不出是完备匹配下的最大权匹配(当然,这个也可以用网络流做。(应该是添加源点、汇点,源点到每个m的距离取m到所有H中最小的那个(用一个大数减掉后就是最大的)汇点到每个H的距离类似,然后求最大流) 有空再试着做一下吧,空说无益)。 我是在图论500题里看到的,在网络流基础题里面。一开始想不出这个怎么流! 后面网上查这个是二分图最优匹配。于是昨天花几个小时看了相关资料,写了
火山引擎数智平台:A/B测试个性化配置能力发布,拓展多场景策略最优解
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 对于这些场景,你一定不会感到陌生:打开手机时,一款购物应用推荐的正好是你心仪已久的商品;浏览网页时,新闻资讯自动排列,展示的都是你最感兴趣的话题;沉浸于在线娱乐时,所呈现的内容仿佛是为你量身定制…… 这一切与“用户个性化配置发布”能力息息相关。“用户个性化配置发布”指根据行为、性别,兴趣、地理位
【深入解析】最优控制中的Bellman方程——从决策到最优路径的探索
【深入解析】最优控制中的Bellman方程——从决策到最优路径的探索 关键词提炼 #Bellman方程 #最优控制 #动态规划 #值函数 #策略优化 #强化学习 第一节:Bellman方程的通俗解释与核心概念 1.1 通俗解释 Bellman方程是动态规划中的一个核心概念,它像是一个“未来价值指南针”,帮助我们在面对一系列决策时,找到从当前状态出发到达目标状态的最优路径。想象一下,你站
OD C卷 - 寻找最优的路测线路
寻找最优的路测线路(200) 给定一个m行、n列的数组(路线网络),每个值代表当前位置的信号质量,越大信号越好;从 [0, 0] 到 [m-1, n-1]位置的路线中,最小值代表当前路线的评分,如8->4->5->9的评分为4;每个位置可以走向上下左右四个方向,不能对角;找出一个网络中的最优路线的评分; 输入描述: 第一行输入行数m; 第二行输入列数n; 第三行开始,每行为信号值s; 1< m,
阵列信号处理2_阵列信号最优处理常用准则(CSDN_20240825)
目录 最小均方误差(Minimum Square Error,MSE)准则 最大信噪比(Maximum Signal Noise Ratio,MSNR)准则 极大似然(Maximum Likehood, ML)准则 最小方差无损响应(Minimum Variance Distortionless Response, MVDR)准则 四种准则之间的关系
数学建模学习(126):基于Python的最优最劣法(BWM)在多标准决策中的应用
文章目录 1. 引言2. 案例2.1 最优最劣法(BWM)的原理2.2 数据来源和定义2.3 Python实现2.4 结果分析 3. 结论参考文献 1. 引言 在现代决策分析中,如何合理地评估和选择多个备选方案是一项复杂的任务。多标准决策分析(MCDA)方法提供了一种科学的途径,通过对多个标准的综合评估,帮助决策者做出最优选择。本文将介绍一种重要的MCDA方法——最优最劣法(B
2024华为OD机试真题-寻找最优的路测线路Python-C卷D卷-200分
2024华为OD机试最新E卷题库-(C卷+D卷+E卷)-(JAVA、Python、C++) 目录 题目描述 输入描述 输出描述 备注 用例1 用例2 题目解析 代码 题目描述 评估一个网络的信号质量,其中一个做法是将网络划分为栅格,然后对每个栅格的信号质量计算。 路测的时候,希望选择一条信号最好的路线(彼此相连的栅格集合)进行演示。 现给出 R 行 C 列的整数
CH6101 最优贸易
描述 C国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为1条。 C国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。 商人阿龙来到C国
大数据演进简史:从数仓到数据中台,谈技术选型最优解
大家好,今天分享的议题主要包括几大内容: 带大家回顾一下大数据在国内的发展,从传统数仓到当前数据中台的演进过程;我个人认为数据中台的核心组成,以及一些技术选型参考;数据研发是数据中台很重要的一环,会分享一些我们在数据研发方面的实践,主要是数据仓库架构与研发方面。 一、大数据演进,从数据仓库到数据中台 第一阶段 21世纪的第一个10年,企业级数据仓库(EDW)从萌芽到蓬勃发展,“IOT”(
一个最优解,完美解决了手势滑动的开始结束和代码滑动的问题
- (void)scrollViewDidEndScrollingAnimation:(UIScrollView *)scrollView{ [NSObject cancelPreviousPerformRequestsWithTarget:self]; //NSLog(@"滑动停止(animation)"); _isScrolling = NO ;
最优二叉树(哈夫曼树)知识点
路径:在一棵树中从一个结点往下到孩子或孙子结点之间的通路 结点的路径长度:从根节点到该节点的路径上分支的数目 树的路径长度:树中每个结点的路径长度之和 结点的权:给树中的结点赋予一个某种含义的值,则该值为该节点的权 结点的带权路径长度:结点的路径长度乘以结点的权 树的带权路径长度(WPL):树中所有叶子结点的带权路径长度 (Weight Path Length) 最优二叉树(哈夫
【Sklearn驯化-环境配置】一文搞懂sklearn建模的最优环境搭建用法
【Sklearn驯化-环境配置】一文搞懂sklearn建模的最优环境搭建用法 本次修炼方法请往下查看 🌈 欢迎莅临我的个人主页 👈这里是我工作、学习、实践 IT领域、真诚分享 踩坑集合,智慧小天地! 🎇 相关内容文档获取 微信公众号 🎇 相关内容视频讲解 B站 🎓 博主简介:AI算法驯化师,混迹多个大厂搜索、推荐、广告、数据分析、数据挖掘岗位 个人申请专利40+,熟练掌握机
文章解读与仿真程序复现思路——电力自动化设备EI\CSCD\北大核心《含氢综合能源系统多目标最优折中分布鲁棒低碳调度》
本专栏栏目提供文章与程序复现思路,具体已有的论文与论文源程序可翻阅本博主免费的专栏栏目《论文与完整程序》 论文与完整源程序_电网论文源程序的博客-CSDN博客https://blog.csdn.net/liang674027206/category_12531414.html 电网论文源程序-CSDN博客电网论文源程序擅长文章解读,论文与完整源程序,等方面的知识,电网论文源程序关注python
553. Optimal Division 最优除法
https://leetcode-cn.com/problems/optimal-division/description/ 思路:x1/x2/…/xn,无论在之间加多少个括号,x1总是作为被除数,x2总是作为除数,因此结果最大的做法是将x3到xn的所有除法转换为乘法,即x1/(x2/…/xn)=x1/x2*x3*…*xn. string optimalDivision(vector<int>
机器学习如何重塑最优定价
点击上方“AI公园”,关注公众号,选择加“星标“或“置顶” 作者:Javier 编译:ronghuaiyang 正文共:4727 字 6 图 预计阅读时间:14 分钟 导读 智能定价是机器学习的非常重要的应用场景,能够为企业带来直接的利益,了解一下吧。 正确定价的挑战性 为商品或服务定价是经济学理论中的一个老问题。对于不同的目标,有大量的定价策略。一家公司可能会寻求最大化每一个单销售或整体
【中文】PDF文档切分\切片\拆分最优方案-数据预处理阶段,为后续导入RAG向量数据库和ES数据库实现双路召回
目的 将PDF文档拆开,拆开后每个数据是文档中的某一段,目的是保证每条数据都有较完整的语义,并且长度不会太长 项目自述 看了很多切分项目,包括langchain、Langchain-Chatchat、、Chinese-LangChain、LangChain-ChatGLM-Webui、ChatPDF、semchunk等等,效果还行,但是不够完美,毕竟他们的对"\n"的优先级设置的较高,使用p