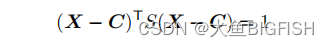拟合专题
OpenCV结构分析与形状描述符(11)椭圆拟合函数fitEllipse()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C++11 算法描述 围绕一组2D点拟合一个椭圆。 该函数计算出一个椭圆,该椭圆在最小二乘意义上最好地拟合一组2D点。它返回一个内切椭圆的旋转矩形。使用了由[90]描述的第一个算法。开发者应该注意,由于数据点靠近包含的 Mat 元素的边界,返回的椭圆/旋转矩形数据
6. 深度学习中的正则化技术:防止过拟合
引言 过拟合是深度学习模型在训练过程中常遇到的挑战。过拟合会导致模型在训练数据上表现良好,但在新数据上表现不佳。为了防止过拟合,研究者们提出了多种正则化技术,如L1/L2正则化、Dropout、数据增强等。这些技术通过约束模型的复杂度或增加数据的多样性,有效提高了模型的泛化能力。本篇博文将深入探讨这些正则化技术的原理、应用及其在实际深度学习任务中的效果。 1. 过拟合的原因与影响 过拟合通常
沐风老师3DMax地形拟合插件使用方法详解
3DMax地形拟合插件使用教程 3DMax地形拟合插件,只需单击几下鼠标,即可将地形表面与道路对齐。它很容易使用。 (注意:如果不仔细阅读,会误认为是这是一个道路拟合(投影)到地形的插件,实际上恰恰相反,这是一个地面拟合到道路的插件。) 【适用版本】 3dMax2010及更高版本 【安
机器学习项目——基于机器学习(RNN LSTM 高斯拟合 MLP)的锂离子电池剩余寿命预测方法研究(代码/论文)
完整的论文代码见文章末尾 以下为核心内容和部分结果 摘要 机器学习方法在电池寿命预测中的应用主要包括监督学习、无监督学习和强化学习等。监督学习方法通过构建回归模型或分类模型,直接预测电池的剩余寿命或健康状态。无监督学习方法则通过聚类分析和降维技术,识别电池数据中的潜在模式和特征。强化学习方法通过构建动态决策模型,在电池运行过程中不断优化预测策略和调整参数。上述方法不仅可以提高预测精度,还可以在
方差(Variance) 偏差(bias) 过拟合 欠拟合
机器学习中方差(Variance)和偏差(bias)的区别?与过拟合欠拟合的关系? (1)bias描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距,简单讲,就是在样本上拟合的好不好。 低偏差和高方差(对应右上图)是使得模型复杂,增加了模型的参数,这样容易过拟合。 这种情况下,形象的讲,瞄的很准,但手不一定稳。 (2)varience描述的是样本上训练出来的模型
人工智能:模型复杂度、模型误差、欠拟合、过拟合/泛化能力、过拟合的检测、过拟合解决方案【更多训练数据、Regularization/正则、Shallow、Dropout、Early Stopping】
人工智能:模型复杂度、模型误差、欠拟合、过拟合/泛化能力、过拟合的检测、过拟合解决方案【更多训练数据、Regularization/正则、Shallow、Dropout、Early Stopping】 一、模型误差与模型复杂度的关系1、梯度下降法2、泛化误差2.1 方差2.2 偏差2.3 噪声2.4 泛化误差的拆分 3、偏差-方差窘境(bias-variance dilemma)4、Bias
深度学习100问43:什么是过拟合
嘿,咱来聊聊过拟合是什么。 想象一下,有个机器学习的模型就像一个学生在准备考试。如果这个模型对训练数据就像学生把课本上的题目背得超级熟,在训练数据上表现得那叫一个棒,就像学生在做课本上的题时成绩超高。但是呢,一旦碰到新的、从来没见过的数据,就傻眼了,表现得一塌糊涂。这时候就可以说这个模型过拟合啦。 为啥会过拟合呢?一方面可能是这个模型太复杂了,就像学生学得太“死”,记住了训练数据里的一些小
过度拟合------正则化
转载: 1. The Problem of Overfitting 1 还是来看预测房价的这个例子,我们先对该数据做线性回归,也就是左边第一张图。 如果这么做,我们可以获得拟合数据的这样一条直线,但是,实际上这并不是一个很好的模型。我们看看这些数据,很明显,随着房子面积增大,住房价格的变化趋于稳定或者说越往右越平缓。因此线性回归并没有很好拟合训练数据。 我们把此类情况称为欠拟合(u
建模杂谈系列249 增量数据的正态分布拟合
说明 从分布开始,分布又要从正态开始 假设有一批数据,只有通过在线的方式增量获得。 内容 1 生成 先通过numpy生成一堆随机数据,从3个正态分布生成,然后拼接起来。 import numpy as npimport matplotlib.pyplot as pltfrom sklearn.mixture import GaussianMixture# 生成示例数据np.
【tensorflow】1.拟合曲线
写demo的时候,遇到一个问题,排查了很久也找不到原因。 若生成训练数据的时候,用这种方式生成 num_points = 1000x = np.linspace(0,10,num_points )y = a * x * x + b * x + c 则在求loss的时候,loss越来越大,至至NAN,排查半天发现,这里linspace参数必须(0,1),也就是x必须0-1之间,才能正常求出
采用不高于3次的勒让德多项式拟合原函数
利用勒让德多项式进行拟合的区域是[-1,1],如果不是这个区域,比如是[a,b],利用转化到[-1,1]。 参考以下例题计算系数 C语言代码如下 //用三阶的勒让德多项式进行拟合#include<math.h>#include<stdio.h>#include "main.c"double f(double x);double fl1(double x);double f
【R语言】基于nls函数的非线性拟合
非线性拟合 1.写在前面2.实现代码 1.写在前面 以下代码记录了立地指数的计算过程,包括了优势树筛选、误差清理、非线性拟合以及结果成图。 优势树木确定以及数据清理过程: 相关导向函数: 2.实现代码 ##*******************************************************************************----
概率统计Python计算:假设检验应用——分布拟合检验
对来自总体 X X X的样本 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn,及给定的显著水平 α \alpha α检验假设 H 0 : X 的分布函数为 F ( x ) ( H 1 : X 的分布函数不是 F ( x ) ) . H_0:X\text{的分布函数为}F(x)(H_1:X\text{的分布函数不是}F(x)). H0:X
正则化方法:防止过拟合,提高泛化能力
本文是《Neural networks and deep learning》概览 中第三章的一部分,讲机器学习/深度学习算法中常用的正则化方法。(本文会不断补充) 正则化方法:防止过拟合,提高泛化能力 在训练数据不够多时,或者overtraining时,常常会导致overfitting(过拟合)。其直观的表现如下图所示,随着训练过程的进行,模型复杂度增加,在training da
机器学习十-欠拟合和过拟合
在机器学习中,欠拟合和过拟合是常见的两个问题,影响模型的性能和泛化能力。理解它们的区别和解决方法对于构建高效的模型至关重要。 欠拟合(Underfitting) 欠拟合指的是模型对训练数据的学习不足,未能捕捉数据中的潜在规律或结构,导致模型在训练集和测试集上的表现都很差。 特点: 模型复杂度低,无法很好地拟合数据。在训练集上表现不好,测试集上的表现同样不好。常见于模型过于简单、特征不足或训
基于NURBS曲线的数据拟合算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 4.1NURBS曲线基础 4.2 数据拟合原理 5.完整程序 1.程序功能描述 基于NURBS曲线的数据拟合算法,非均匀有理B样条(Non-Uniform Rational B-Splines,简称NURBS)曲线是一种强大的数学工具,广泛应用于计算机图形学、CAD/CA
B样条曲线曲面--拟合技术
B样条曲线曲面 1.B样条曲线 B样条曲线(B-spline curve)是一种在计算机图形学和计算几何中广泛使用的参数曲线。它是贝塞尔曲线(Bezier curve)的一种推广,提供了更好的局部控制能力。B样条曲线由一组控制点(也称为控制顶点)和一组基函数(称为B样条基函数)定义。 1.1.B样条曲线的定义 给定一组 ( n + 1 ) 个控制点 ( P i ) 和一组节点( k n
Bezier曲线曲面--拟合技术
Bezier曲线曲面–拟合应用 1.Bezier曲线 1.1.Bezier曲线的定义 给定一组控制点 P_0, P_1, …, P_n,其中 n 是曲线的阶数,Bezier曲线的参数方程可以表示为: B ( t ) = ∑ i = 0 n P i b i , n ( t ) , t ∈ [ 0 , 1 ] B(t) = \sum_{i=0}^{n} P_i b_{i,n}(t), \qua
有理B样条曲线曲面(NURBS)--拟合技术
非有理B样条曲线曲面(NURBS) 1.NURBS曲线 NURBS(Non-Uniform Rational B-Spline)曲线是一种在计算机辅助设计(CAD)和计算机图形学中广泛使用的数学表示方法,用于精确地定义和渲染复杂的曲线和曲面。NURBS曲线结合了B-Spline曲线和Bezier曲线的优点,提供了对曲线形状的精确控制以及对曲线几何和拓扑属性的灵活操作。 1.1.NURBS曲线
【matlab】数据拟合
一、拟合的概念 数据拟合又称曲线拟合,俗称拉曲线,是一种把现有数据透过数学方法来代入一条数式的表示方式。科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合(fitting)。 二、曲线拟合matlab实现 1.多项式函数拟合: a=polyfit(xdata,yda
MATLAB数据拟合中的若干问题(待续)
1. 多项式拟合 多项式拟合的形式如下: y=∑i=1Npixn−i+1=p1xn+p2xn−1+⋅⋅⋅+pnx+pn+1 y=\sum_{i=1}^Np_ix^{n-i+1}=p_1x^n+p_2x^{n-1}+···+p_nx+p_{n+1} 其中 p p为权重向量P=[p1,p2,⋅⋅⋅,pn,pn+1]\mathbf{P}=[p_1,p_2,···,p_n,p_
PCL 拟合二维椭圆(迭代法)
文章目录 一、简介二、实现代码三、实现效果参考资料 一、简介 一般情况,我们会用椭圆拟合二维点,用椭球拟合三维点。在n维中,这些对象被称为超椭球体,由二次方程隐式定义 超椭球的中心是n×1向量C,n×n矩阵S是正定的,n×1向量X是超椭球上的任意点。矩阵S可以用特征分解,S = R D R T RDR^T RD