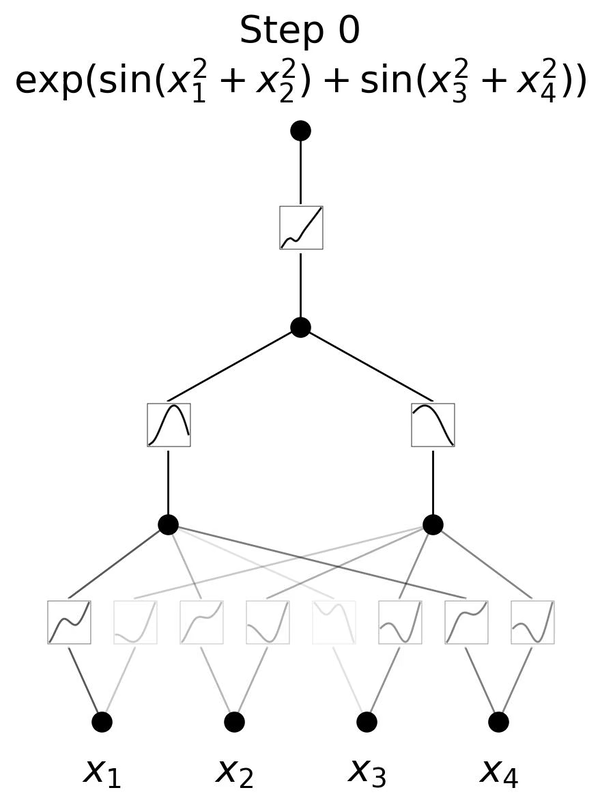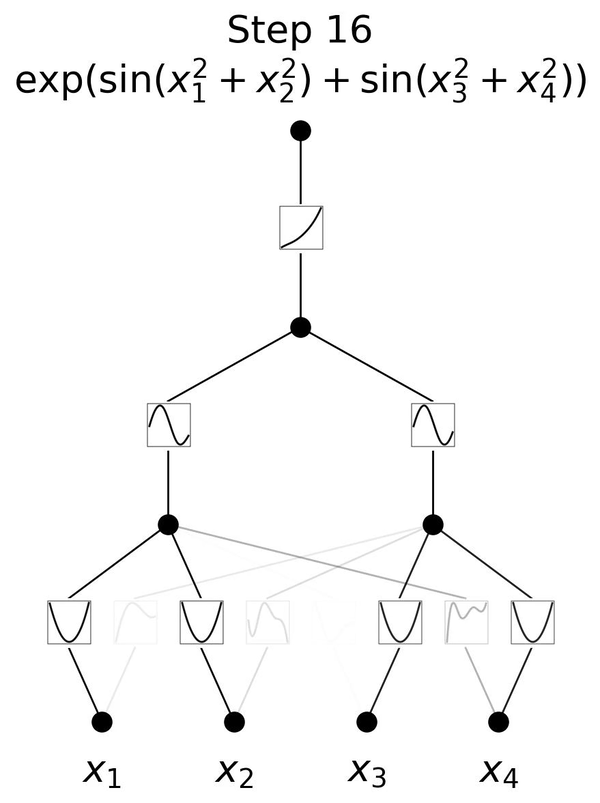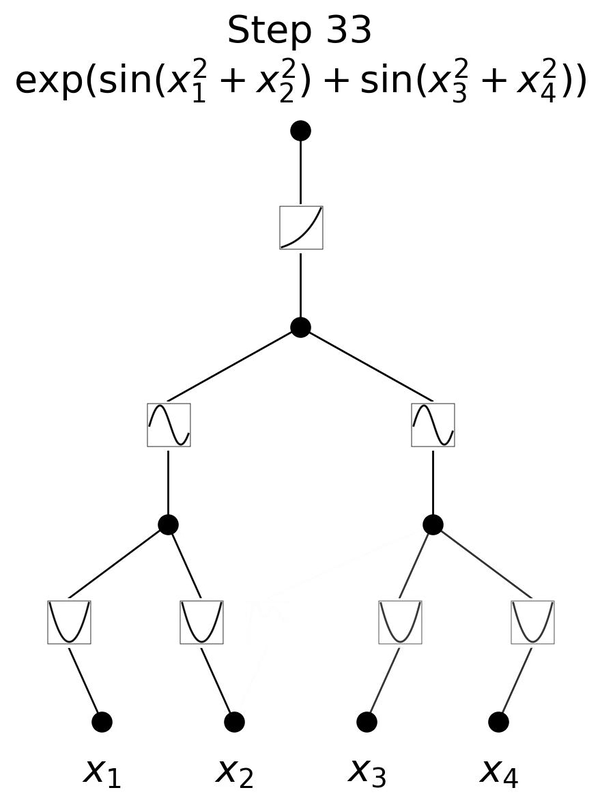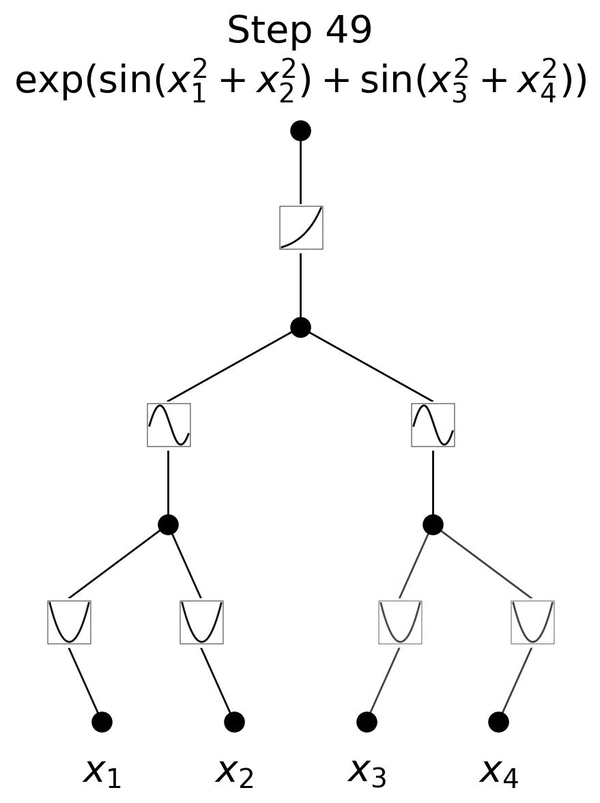
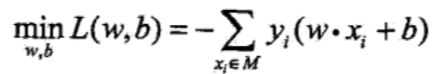感知机专题
【2.1 深度学习中的感知机是什么】
2.1 深度学习中的感知机是什么 深度学习是机器学习的一个分支,它模拟人脑的工作方式来处理数据,尤其是通过神经网络的结构来自动提取数据的特征并进行分类、回归或其他复杂的任务。在深度学习的早期发展中,许多基础概念和模型为后续的复杂网络奠定了基础。其中,**感知机(Perceptron)**是一个非常重要的基础模型,它实际上是神经网络和深度学习的前身之一。 感知机的基本概念 感知机是一种二分
Tensorflow实现与门感知机
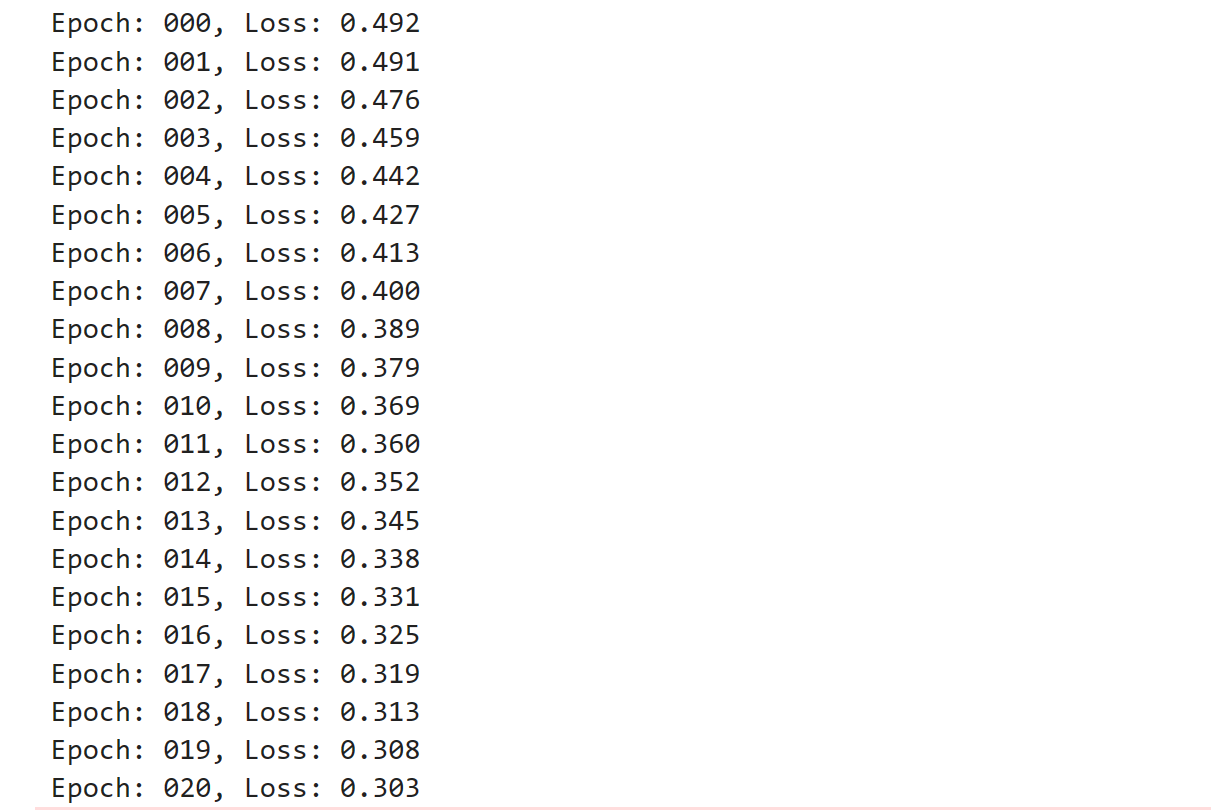
感知机是最简单的神经网络,通过输入,进行加权处理,经过刺激函数,得到输出。通过输出计算误差,调整权重,最终,得到合适的加权函数。 今天,我通过tensorflow实现简单的感知机。 首先,初始化变量: num_nodes = 2 output_units = 1 w = tf.Variable(tf.truncated_normal([num_nodes,output
(感知机-Perceptron)—有监督学习方法、非概率模型、判别模型、线性模型、参数化模型、批量学习、核方法
定义 假设输入空间(特征空间)是 χ \chi χ ⊆ R n \subseteq R^n ⊆Rn,输出空间是y = { + 1 , − 1 } =\{+1,-1 \} ={+1,−1} 。输入 x ∈ χ x \in \chi x∈χ表示实例的特征向量,对应于输入空间(特征空间)的点;输出 y ∈ y \in y∈y表示实例的类别。由输入空间到输出空间的如下函数: f ( x ) = s
【技术干货】一文搞懂感知机算法:从理论到Python实战
一 引言 在机器学习中,感知机(perceptron)是二分类的线性分类模型,属于监督学习算法。输入为实例的特征向量,输出为实例的类别(取+1和-1)。感知机对应于输入空间中将实例划分为两类的分离超平面。感知机旨在求出该超平面,为求得超平面导入了基于误分类的损失函数,利用梯度下降法对损失函数进行最优化(最优化)。感知机的学习算法具有简单而易于实现的优点,分为原始形式和对偶形式。感知机预测是用学习
【机器学习-监督学习】神经网络与多层感知机
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈Python机器学习 ⌋ ⌋ ⌋ 机器学习是一门人工智能的分支学科,通过算法和模型让计算机从数据中学习,进行模型训练和优化,做出预测、分类和决策支持。Python成为机器学习的首选语言,依赖于强大的开源库如Scikit-learn、TensorFlow和PyTorch。本专栏介绍机器学习的相关算法以及基于Python的算法实现。
机器学习第一篇----感知机
《统计学习方法》看到第三遍,准备给大家分享一下感悟,已经一些算法的代码实现 首先来看下《统计学习方法》对感知机的定义 其实我们想象一下,就是一条线(直线<线性可分>,曲线都可以<非线性可分>),把空间一分为二,很容易理解。 f(x) 是一个激励函数,经过拟合的参数w,b计算,输入的x,然后就可以将X的空间分为{+1,-1}。 但是w,b什么时候达到最优呢?看下面的算法: 注意:y
神经网络第一篇:激活函数是连接感知机和神经网络的桥梁
前面发布的文章介绍了感知机,了解了感知机可以通过叠加层表示复杂的函数。遗憾的是,设定合适的、能符合预期的输入与输出的权重,是由人工进行的。从本章开始,将进入神经网络的学习,首先介绍激活函数,因为它是连接感知机和神经网络的桥梁。如果读者认知阅读了本专题知识,相信你必有收获。 感知机数学表达式的简化 前面我们介绍了用感知机接收两个输入信号的数学表示如下:
多层感知机不等于神经网络?
在前一章节(https://blog.csdn.net/u012132349/article/details/86166324),我们介绍了感知机可以实现与门、或门、非门。只需给定合适的参数(w1, w2, b)并利用Python就可以简单实现对输入的任意(x1,x2),输出0或1。 今天我们将介绍感知机的局限性(严格说是单层感知机的局限性)。这里我们想用感知机实现异或门,所谓异
动手学深度学习(Pytorch版)代码实践 -深度学习基础-08多层感知机简洁版
08多层感知机简洁版 import torchfrom torch import nnfrom d2l import torch as d2limport liliPytorch as lpnet = nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),nn.Linear(256,10) )#函数接受一个参数 m,通常是一个神
《李航:统计学习方法》笔记之感知机
感知机学习旨在求出将训练数据集进行线性划分的分类超平面,为此,导入了基于误分类的损失函数,然后利用梯度下降法对损失函数进行极小化,从而求出感知机模型。感知机模型是神经网络和支持向量机的基础。也是现代流行的深度学习网络模型的基础。下面分别从感知机学习的模型、策略和算法三个方面来介绍。 1. 感知机模型 感知机模型如下: f(x)= sign(w*x+b) 其中,x
【动手学深度学习】多层感知机之暂退法研究详情
目录 🌊1. 研究目的 🌊2. 研究准备 🌊3. 研究内容 🌍3.1 多层感知机暂退法 🌍3.2 基础练习 🌊4. 研究体会 🌊1. 研究目的 防止过拟合:权重衰减和暂退法都是用来控制模型的复杂度,防止模型在训练集上过拟合;提高模型泛化能力:通过在训练过程中应用权重衰减或暂退法,可以限制模型对训练数据的过度依赖,从而提高模型在未见过的测试数据上
【动手学深度学习】多层感知机之暂退法问题研究详情
目录 🌊问题研究1 🌞问题研究2 🌲问题研究3 🌍问题研究4 🌳问题研究5 🌌问题研究6 🌊问题研究1 如果更改第一层和第二层的暂退法概率,会发生什么情况?具体地说,如果交换这两个层,会发生什么情况?设计一个实验来回答这些问题,定量描述该结果,并总结定性的结论 在原始的代码中,首先应用了nn.Linear层,然后在第一个全连接层之后添加了
Pytorch实用教程:pytorch中nn.Linear()用法详解 | 构建多层感知机 | nn.Module的作用 | nn.Sequential的作用
文章目录 1. nn.Linear()用法构造函数参数示例使用场景 2. 构建多层感知机步骤代码示例注意事项 3. 继承自nn.Module的作用是什么?1. 组织网络结构2. 参数管理3. 模型保存和加载4. 设备管理不继承 `nn.Module` 的后果
统计学习方法笔记-感知机
感知机是二类分类的线性模型,其输入为实例的特征向量,输出为实例的类别,取+1和-1二值,属于判别模型。分为原始形式和对偶形式。是神经网络与支持向量机的基础。 由输入空间到输出空间的如下函数:f(x) = sign(w·x + b) 称为感知机. 其中,w和b为感知机模型参数, 叫做权值或权值向量, 叫做偏置, sign是符号函数,即
【深度学习】2.单层感知机
目标: 实现一个简单的二分类模型的训练过程,通过模拟数据集进行训练和优化,训练目标是使模型能够根据输入特征正确分类数据。 演示: 1.通过PyTorch生成了一个模拟的二分类数据集,包括特征矩阵data_x和对应的标签数据data_y。标签数据通过基于特征的线性组合生成,并转换成独热编码的形式。 import torch# 从torch库中导入神经网络模块nn,用于构建神经网络模
机器学习实战——感知机
感知机学习策略具体实现 数据集最大最小规范化训练过程测试最终结果 感知机是二分类的线性分类模型,由Rosenblatt于1957年提出,是支持向量机和神经网络的基础。感知机将学习到一个线性划分的分离超平面,属于判别模型。 感知机 输入空间为 Rn R^n空间, n n是特征数目,输出空间y={+1,−1}y=\{+1,-1\}。感知机学习一个如下的符号函数: f
前馈神经网络FNN、多层感知机MLP和反向传播推导
目录 一、前馈神经网络FNN 激活函数的使用 二、多层感知机MLP MLP的典型结构 多层感知机MLP的特点 和前馈神经网络FNN的区别 三、传播推导 1、前向传播(Forward propagation) (1)输入层到隐藏层 (2)隐藏层到输出层 2、反向传播(Backward propagation) (1)正向传播(Forward Pass) (2)反向传播(Ba
4. 从感知机到神经网络
目录 1. 从感知机到神经网络 2. 最简单的神经网络 3. 激活函数的引入 1. 从感知机到神经网络 之前章节我们了解了感知机,感知机可以处理与门、非与门、或门、异或门等逻辑运算;不过在感知机中设定权重的工作是由人工来做的,而设定合适的,符合预期的输入与输出的权重,是一项非常繁重的工作。神经网络就是为了实现这一工作,它的一个重要性质就是可以自动的从数据中学到合适
动手学深度学习——多层感知机
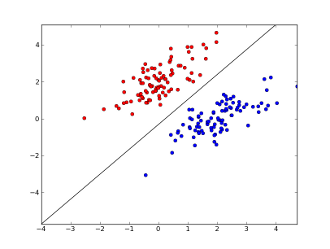
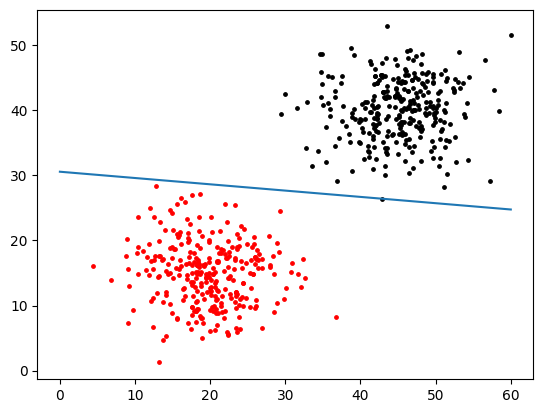
1. 感知机 感知机本质上是一个二分类问题。给定输入x、权重w、偏置b,感知机输出: 以猫和狗的分类问题为例,它本质上就是找到下面这条黑色的分割线,使得所有的猫和狗都能被正确的分类。 与线性回归和softmax的不同点: vs 线性回归:输出的都是一个数,但线性回归输出的是实数,而感知机输出的是离散的分类。vs softmax: softmax是一个多分类(如果有n个分类,softmax
机器学习:感知机--Perceptron
机器学习:感知机–Perceptron 感知器是具有二进制输入和阶梯激活函数的神经元。 输入:0或者1 输出:0或者1 激活函数:阶梯函数 举例 (1)与门 H(x)表示阶梯函数,或者说Heaviside函数 y = H ( x 1 + x 2 − 1.5 ) y = H(x_1+x_2-1.5) y=H(x1+x2−1.5) (2)或门 y = H ( x 1 + x
【Kolmogorov-Arnold网络 替代多层感知机MLPs】KAN: Kolmogorov-Arnold Networks
KAN: Kolmogorov-Arnold Networks 论文地址 代码地址 知乎上的讨论(看一下评论区更正) Abstract Inspired by the Kolmogorov-Arnold representation theorem, we propose Kolmogorov-Arnold Networks (KANs) as promising alternati
神经网络的基础:从感知机到复杂网络的进化
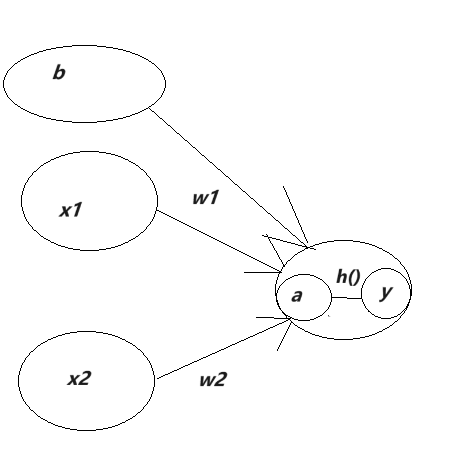
文章目录 一、神经网络的例子二、理解神经信号的传递2.1 感知机的结构和功能2.2 优化函数2.3 明确表示偏置 三、理解感知机和激活函数的作用3.1 基础感知机模型3.2 激活函数的引入 一、神经网络的例子 理解感知机 在探索神经网络之前,我们首先回顾了感知机的基本概念。感知机是一种二分类的线性分类模型,它的基本功能是将输入的特征向量转化为一个预测结果。虽然感知机在理论
语音识别--基于MFCC和多层感知机的语音情感识别
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计3077字,阅读大概需要3分钟 🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿 个人网站:https://jerry-jy.co/ ❗❗❗知识付费,🈲止白嫖,有需要请后台私信或【文末】个人微信公众号联系我 语音识别--基于MFCC和多层感知机的语音情感识别 基于MFCC和多
多层感知机(MLP)示例
通过5个条件判定一件事情是否会发生,5个条件对这件事情是否发生的影响力不同,计算每个条件对这件事情发生的影响力多大,写一个多层感知机模型pytorch程序,最后打印5个条件分别的影响力。 一 在多层感知机(MLP)模型中,输入特征(本例中的5个条件)通过多个全连接层进行非线性变换,最终产生输出。与线性模型不同,MLP能够学习特征之间的复杂交互,并且通过隐藏层的激活函数引入非线性。 影响