统计学习-感知机

本文主要是介绍统计学习-感知机，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

感知机(perceptron)是二类分类的线性模型，其输入为实例的特征向量，输出为实例的类别，取值（-1，+1）。感知机由1957年Rosenblatt提出，是神经网络和SVM的基础。

1.感知机模型：
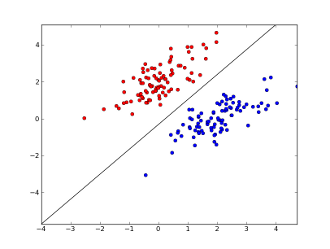
$f(x)=sign(w*x+b)$对应于下图中的黑线，专业术语就是分离超平面（separating hyperplane）.红色点标记为+1，蓝色点标记为-1。感知机可以处理的问题是数据是线性可分的（线性不可分的经典例子就是异或问题）。

2.感知机学习策略：定义损失函数并将损失函数极小化。感知机定义的损失函数：
$L(w,b) = - \sum_{x_i\epsilon M} y_i(w*x_{0}+b)$这就是函数距离。该损失函数对于参数$w和b$都是连续可导函数。所以我们需要寻找$w^*和b^*$使得损失函数极小化;
3.感知机学习算法：感知机学习问题转化为求解损失函数的最优化问题，而求解最优化问题最典型的就是梯度下降法：
代价函数：$L(w,b) = - \sum_{x_i\epsilon M} y_i(w*x_{0}+b)$
对参数$w和b$求梯度：
$\frac{\partial L(w,b)}{\partial w} = - \sum_{x_i\epsilon M}y_ix_i$
$\frac{\partial L(w,b)}{\partial b} = - \sum_{x_i\epsilon M}y_i$
而参数$w和b$的更新基于以下公式：
$w \leftarrow w + \eta y_ix_i$
$b \leftarrow b + \eta y_i$
故可以确定最终的参数$w和b$：
$w={\eta}\sum_{i=1}^{N}{\alpha_i}y_ix_i$
$b={\eta}\sum_{i=1}^{N}{\alpha_i}x_i$
其中的$\alpha_i$表示第i个实例点由于误分而进行更新的次数，实例点更新次数越多，意味着它离超平面越近，也就越难正确分类。
4.感知器算法的对偶形式：
输入：已知样本集$T=\{(x_i,y_i)\}$和学习率$\eta$
输出：$\alpha和b$;感知机模型：$f(x)=sign(\sum_{i=1}^{N}{\alpha_i}y_ix_i*x+b)$
对偶形式中训练实例仅以内积的形式出现。（个人感觉可以引入核函数处理线性不可分的情况，但是前段时间面试网易的时候直接被否决了）

这篇关于统计学习-感知机的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---