本文主要是介绍【技术干货】一文搞懂感知机算法:从理论到Python实战,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一 引言
在机器学习中,感知机(perceptron)是二分类的线性分类模型,属于监督学习算法。输入为实例的特征向量,输出为实例的类别(取+1和-1)。感知机对应于输入空间中将实例划分为两类的分离超平面。感知机旨在求出该超平面,为求得超平面导入了基于误分类的损失函数,利用梯度下降法对损失函数进行最优化(最优化)。感知机的学习算法具有简单而易于实现的优点,分为原始形式和对偶形式。感知机预测是用学习得到的感知机模型对新的实例进行预测的,因此属于判别模型。感知机由Rosenblatt于1957年提出的。
在神经网络、支持向量机等算法盛行的当下,感知机模型应用得并不多,但必须承认,感知机却是神经网络和支持向量机的基础,所以还是很有必要学习一下的,本文接下来的内容将从感知机数学描述、损失函数、两种不同学习形式等方面详细介绍感知机,最后使用Python实现感知机两种学习形式。
二 感知机模型及损失函数
2.1 定义
对于给定训练样本数据集 D = { ( x i , y i ) } i = 1 m D = \{ ({x_i},{y_i})\} _{i = 1}^m D={(xi,yi)}i=1m, x i ∈ X ⊆ R n {x_i} \in X \subseteq {R^n} xi∈X⊆Rn表示训练样本的特征向量,${y_i} \in Y = { + 1, - 1} 表示样本类别。 表示样本类别。 表示样本类别。x 与 与 与y$之间的如下函数关系:
y = f ( x ) = s i g n ( w ⋅ x + b ) y = f(x) = sign(w \cdot x + b) y=f(x)=sign(w⋅x+b)
称为感知机。其中, w ∈ R n w \in {R^n} w∈Rn称为感知机的权值系数或者权值向量weight, b ∈ R b \in R b∈R称为偏置bias, w ⋅ x w⋅x w⋅x表示 w w w和 x x x的点积
∑ i = 1 m w i x i = w 1 x 1 + w 2 x 2 + . . . + w n x n \sum_{i=1}^m w_i x_i= w_1x_1+w_2x_2+...+w_nx_n i=1∑mwixi=w1x1+w2x2+...+wnxn
s i g n sign sign是符号函数,有:
f ( x ) = { − 1 , x < 0 + 1 , x ⩾ 0 f(x) = \left\{ {_{ - 1, x < 0}^{ + 1, x \geqslant 0}} \right. f(x)={−1,x<0+1,x⩾0
从定义上可以看出,感知机最终目标就是求解出 w w w和 b b b。我们可以从几何上对感知机进行理解,如果以 w w w为法向量,以 b b b为截距,可以确定一超平面:
w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0
通过这一超平面,可以顺利将对数据集进行划分。
以二维数据为例,如下图所示,当样本点 x x x刚好落在超平面上时,有 w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0,当 x x x落在超平面下方时,有 w ⋅ x + b < 0 w \cdot x + b < 0 w⋅x+b<0,通过 s i g n sign sign函数后输出为 − 1 -1 −1,也就是标记为 − 1 -1 −1类;当 x x x落在超平面上方时,有 w ⋅ x + b > 0 w \cdot x + b > 0 w⋅x+b>0,通过 s i g n sign sign函数后输出为 + 1 +1 +1,也就是标记为 + 1 +1 +1类。

注意,这样的超平面一般不唯一,也就是说感知机最终解可以有很多个,受参数初始值、训练样本输入顺序等因素的影响,每次训练时所获得的超平面都可能不一样。
2.2 损失函数
为了求解参数 w w w和 b b b,确定最终的分割超平面,我们需要定义一个目标函数或者说损失函数,通过最小化损失函数来达到目的。在感知机模型中,以误分类的样本对象与分割超平面间的距离之和最为损失函数。我们高中时学过,对于点 ( x 0 , y 0 ) ({x_0},{y_0}) (x0,y0),到平面 A ⋅ x + B ⋅ y + C = 0 A \cdot x + B \cdot y + C = 0 A⋅x+B⋅y+C=0的距离为:
d i s t = ∣ A ⋅ x 0 + B ⋅ y 0 + C ∣ A 2 + B 2 dist = \frac{{|A \cdot {x_0} + B \cdot {y_0} + C|}}{{\sqrt {{A^2} + {B^2}} }} dist=A2+B2∣A⋅x0+B⋅y0+C∣
将这一公式扩展到超平面中,对于超平面 w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0,误分类点 x i x_i xi到超平面的距离为:
d i s t = ∣ w ⋅ x i + b ∣ ∥ w ∥ dist = \frac{{|w \cdot xi + b|}}{{\left\| w \right\|}} dist=∥w∥∣w⋅xi+b∣
式中, ∥ w ∥ {\left\| w \right\|} ∥w∥是 w w w的 L 2 L_2 L2范数,等同于上面的 A 2 + B 2 {\sqrt {{A^2} + {B^2}} } A2+B2。
为了方便计算,我们需要将分子中的绝对值去掉,怎么去掉呢?因为 ( x i , y i ) ({x_i},{y_i}) (xi,yi)是误分类样本点, y i y_i yi与 w ⋅ x i + b {w \cdot xi + b} w⋅xi+b一定是异号的,所以:
$$
- {y_i} \cdot (w \cdot x_i + b) > 0
$$
且因为 ∣ y i ∣ = 1 |{y_i}| = 1 ∣yi∣=1,所以:
$$
- {y_i} \cdot (w \cdot x_i + b) = |w \cdot x_i + b|
KaTeX parse error: Can't use function '$' in math mode at position 5: 于是,$̲({x_i},{y_i})$到…
\frac{{ - {y_i} \cdot (w \cdot x_i + b)}}{{\left| w \right|}}
KaTeX parse error: Can't use function '$' in math mode at position 4: 假设$̲M$是所有误分类点组成的集合,…
\sum\limits_{{x_i} \in M} {\frac{{ - {y_i} \cdot (w \cdot {x_i} + b)}}{{\left| w \right|}}} \tag{1}
KaTeX parse error: Can't use function '$' in math mode at position 38: …是雏形,是因为我们还可以通过令$̲\left\| w \righ…
L(w,b) = \sum\limits_{{x_i} \in M} { - {y_i} \cdot (w \cdot {x_i} + b)} \tag{2}
$$
L ( w , b ) L(w,b) L(w,b)就是我们最终需要的损失函数。
为什么可以直接令 ∥ w ∥ = 1 \left\| w \right\|{\text{ = }}1 ∥w∥ = 1来化简式(1)呢?
我们可以在权值向量 w w w中添加一个 w 0 w_0 w0元素,在特征向量 x i x_i xi中添加一个第0纬度 x ( 0 ) = 1 {x^{(0)}} = 1 x(0)=1,令偏置 b = w 0 ⋅ x ( 0 ) b = {w_0} \cdot {x^{(0)}} b=w0⋅x(0),这样,我们就把偏置 b b b也放进了权值向量 w w w中,那式(1)就变为:
∑ x i ∈ M − y i ⋅ w ⋅ x i ∥ w ∥ \sum\limits_{{x_i} \in M} {\frac{{ - {y_i} \cdot w \cdot {x_i}}}{{\left\| w \right\|}}} xi∈M∑∥w∥−yi⋅w⋅xi
此时,分子和分母都含有 w w w,当分子的 w w w扩大 N N N倍时,分母的 L 2 L_2 L2范数也会扩大N倍。也就是说,分子和分母有固定的倍数关系。那么我们可以固定分子或者分母为1,然后求分母的倒数或者分子自己的最小化作为损失函数,这样可以简化我们的损失函数。在感知机模型中,采用的是保留分子的策略。
另一种解释,当把偏置 b b b包含进 w w w后,超平面表达式也简化成 w ⋅ x i = 0 w \cdot {x_i} = 0 w⋅xi=0,无论是把 w w w扩大多少倍、缩小多少倍,都对超平面没有影响(就像 x + y − 1 = 0 x + y - 1 = 0 x+y−1=0与 2 x + 2 y − 2 = 0 2x + 2y - 2 = 0 2x+2y−2=0始终表示同一条直线),那么我们总能找到一个倍数,将 w w w缩小到满足 ∥ w ∥ = 1 {\left\| w \right\|}=1 ∥w∥=1,但并不影响我们获得最终的超平面,但是令 ∥ w ∥ = 1 {\left\| w \right\|}=1 ∥w∥=1后却有助于我们化简和求解。
三 优化方法
上一节中,我们介绍了感知机模型损失函数 L ( w , b ) L(w,b) L(w,b)的由来,接下来就要说说怎么通过优化损失函数来获得最终的超平面。在感知机模型中,有两种优化方式:原始形式和对偶形式。
3.1 原始形式
原始形式采用的是梯度下降法进行求解,如果对梯度下降法不了解,可以参看前面写过的一篇梯度下降法。这里需要注意的是,在上一小节中说过,感知机是基于误分类驱动的一种模型,所以不能使用整个数据集进行梯度下降优化,只能对误分类样本集合 M M M采用随机梯度下降法或者小批量梯度下降法进行优化。
对损失函数 L ( w , b ) L(w,b) L(w,b)求偏导:
∂ L ( w , b ) ∂ w = − ∑ x i ∈ M y i ⋅ x i \frac{{\partial L(w,b)}}{{\partial w}} = - \sum\limits_{{x_i} \in M} {{y_i} \cdot {x_i}} ∂w∂L(w,b)=−xi∈M∑yi⋅xi
∂ L ( w , b ) ∂ b = − ∑ x i ∈ M y i \frac{{\partial L(w,b)}}{{\partial b}} = - \sum\limits_{{x_i} \in M} {{y_i}} ∂b∂L(w,b)=−xi∈M∑yi
那么, w w w的梯度下降迭代公式为:
w = w + α ⋅ ∑ x i ∈ M y i ⋅ x i w = w + \alpha \cdot \sum\limits_{{x_i} \in M} {{y_i} \cdot {x_i}} w=w+α⋅xi∈M∑yi⋅xi
偏置 b b b的梯度下降迭代公式为:
b = b + α ⋅ ∑ x i ∈ M y i b = b + \alpha \cdot \sum\limits_{{x_i} \in M} {{y_i}} b=b+α⋅xi∈M∑yi
式中,$\alpha 是学习率。感知机模型中,一般采用随机梯度下降法进行优化,每次使用一个误分类样本点进行梯度更新。假设 是学习率。 感知机模型中,一般采用随机梯度下降法进行优化,每次使用一个误分类样本点进行梯度更新。假设 是学习率。感知机模型中,一般采用随机梯度下降法进行优化,每次使用一个误分类样本点进行梯度更新。假设(x_i,y_i) 是 是 是M$中的一个误分类点,进行梯度更新:
w = w + α ⋅ y i x i (3) w = w + \alpha \cdot {y_i}{x_i} \tag{3} w=w+α⋅yixi(3)
b = b + α ⋅ y i (4) b = b + \alpha \cdot {y_i} \tag{4} b=b+α⋅yi(4)
总结一下原始形式优化步骤。
输入:训练样本数据集 D = { ( x i , y i ) } i = 1 m D = \{ ({x_i},{y_i})\} _{i = 1}^m D={(xi,yi)}i=1m, x i ∈ X ⊆ R n {x_i} \in X \subseteq {R^n} xi∈X⊆Rn,${y_i} \in Y = { + 1, - 1} $,学习率% α ∈ ( 0 , 1 ) \alpha \in (0,1) α∈(0,1)
输出: w w w, b b b;感知机模型$f(x) = sign(w \cdot x + b) $
- 初始化 w 0 w_0 w0, b 0 b_0 b0;
- 在 D D D中选取任意点 ( x i , y i ) (x_i,y_i) (xi,yi);
- 通过 y i ⋅ ( w ⋅ x i + b ) {y_i} \cdot (w \cdot {x_i} + b) yi⋅(w⋅xi+b)的值判断是否是误分类点,如果是,使用式(3)、(4)更新参数;
- 回到步骤2直到准确率满足条件。
3.2 对偶形式
对偶形式时原始形式在执行效率上的优化。通过3.1小节中,我们知道,每当一个样本点 x i x_i xi被错误分类一次时,都会使用式(3)(4)更新一次参数,那么,如果样本点 x i x_i xi在迭代过程中被错误分类多次(假设 n i n_i ni次),那么就回有 n i n_i ni次参与到参数更新中,我们假设参数 w w w和 b b b的初始值都为0向量,那么,最终获得的参数 w w w和 b b b为:
w = ∑ i = 1 N β i y i x i (5) w = \sum\limits_{i = 1}^N {{\beta _i} {y_i}{x_i}} \tag{5} w=i=1∑Nβiyixi(5)
b = ∑ i = 1 N β i y i (6) b = \sum\limits_{i = 1}^N {{\beta _i} {y_i}} \tag{6} b=i=1∑Nβiyi(6)
这是在对偶形式中的参数更新方式,式中, β i = n i α {\beta _i} ={n_i}\alpha βi=niα。另外,在原始形式中,我们使用 y i ( w ⋅ x i + b ) ⩽ 0 {y_i}(w \cdot {x_i} + b) \leqslant 0 yi(w⋅xi+b)⩽0来判断样本点 x i x_i xi是否被错误分类,将式(5)(6)代入这一判别式中,得:
y i ( ∑ i = 1 N β i y i x i ⋅ x j + ∑ i = 1 N β i y i ) ⩽ 0 (7) {y_i}(\sum\limits_{i = 1}^N {{\beta _i} {y_i}{x_i}} \cdot {x_j} + \sum\limits_{i = 1}^N {{\beta _i} {y_i}}) \leqslant 0 \tag{7} yi(i=1∑Nβiyixi⋅xj+i=1∑Nβiyi)⩽0(7)
在对偶形式中,采用式(7)判断样本点是否正确分类,观察后可以发现,式(7)中有两个样本点 x i x_i xi和 x j x_j xj内积计算,这个内积计算的结果在下面的迭代过程中需要多次被重复使用,如果我们事先用矩阵运算计算出所有的样本之间的内积,那么在算法迭代过程中, 仅仅一次的矩阵内积运算比原始形式中每遍历一个样本点都要计算 w w w与 x i x_i xi的内积要省时得多,这也是对偶形式的感知机模型比原始形式优的原因。
在感知机模型中,样本的内积矩阵称为Gram矩阵,它是一个对称矩阵,记为 G = [ x i , x j ] m × m G = {[{x_i},{x_j}]_{m \times m}} G=[xi,xj]m×m。
总结一下对偶形式的步骤。
输入:训练样本数据集 D = { ( x i , y i ) } i = 1 m D = \{ ({x_i},{y_i})\} _{i = 1}^m D={(xi,yi)}i=1m, x i ∈ X ⊆ R n {x_i} \in X \subseteq {R^n} xi∈X⊆Rn,${y_i} \in Y = { + 1, - 1} $,学习率% α ∈ ( 0 , 1 ) \alpha \in (0,1) α∈(0,1)
输出: w w w, b b b;感知机模型$f(x) = sign(w \cdot x + b) $
(1)初始化所有 n i n_i ni值为0;
(2)计算Gram矩阵;
(3)在 D D D中选取任意点 ( x i , y i ) (x_i,y_i) (xi,yi);
(4)如果 y i ( ∑ i = 1 N β i y i x i ⋅ x j + ∑ i = 1 N β i y i ) ⩽ 0 {y_i}(\sum\limits_{i = 1}^N {{\beta _i} {y_i}{x_i}} \cdot {x_j} + \sum\limits_{i = 1}^N {{\beta _i} {y_i}}) \leqslant 0 yi(i=1∑Nβiyixi⋅xj+i=1∑Nβiyi)⩽0,令 β i = β i + α {\beta _i} = {\beta _i} + \alpha βi=βi+α;
(5)检查是否还有误分类样本点,如果有,回到步骤(2);如果没有,(5)(6)计算 w w w、 b b b最终值。
四 算法实现
# 导入包
import numpy as np
import matplotlib.pyplot as plt
import copy
# 先来制造一批数据
a = np.random.normal(20,5,300)
b = np.random.normal(15,5,300)
cluster1 = np.array([[x, y, -1] for x, y in zip(a,b)])
a = np.random.normal(45,5,300)
b = np.random.normal(40,5,300)
cluster2 = np.array([[x, y, 1] for x, y in zip(a,b)])
dataset = np.append(cluster1,cluster2, axis=0)
for i in dataset:plt.scatter(i[0], i[1],c='black',s=6)
plt.show()

len(dataset)
600
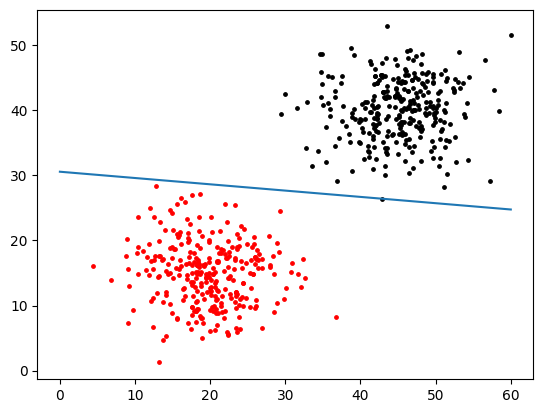
class Perception(object):def __init__(self):"""感知机模型"""self.w = 0self.b = 0def fit_raw_mod(self, train_data, lr=1, max_epoch=None, min_error_rate=0):"""原始模式的感知机训练方法,当达到最大迭代次数或错误率降到最小范围退出train_data:训练数据集lr:学习率max_epoch:最大迭代次数min_error_rate:最小错误率"""self.w = np.zeros(train_data.shape[1]-1) # 根据训练集维度初始化权重系数epoch = 1 # 记录迭代次数while True:error_count = 0 # 记录错误分类样本数for sample in train_data:xi = sample[0:-1]yi = sample[-1]distance = yi * (self.w @ xi + self.b) # yi*(w⋅xi*+b)if distance <= 0: # 对于判断错误的样本点self.w += lr * sample[-1] * sample[0:-1]self.b += lr * sample[-1]error_count += 1# 每完成一次迭代之后,验证一次准确率,准确率达标则退出current_error_rate = float(error_count) / train_data.shape[0]# print('epoch {0},current_error_rate: {1}'.format(epoch+1, current_error_rate))# print('w:{0}, b:{1}'.format(self.w, self.b))# self.show_graph(train_data) # 每一次迭代都展示一次图像if current_error_rate <= min_error_rate:breakif isinstance(max_epoch, int) and epoch >= maxepoch:breakepoch += 1print('w:{0}, b:{1}'.format(self.w, self.b))self.show_graph(train_data)def fit_dual_mod(self,train_data,lr=1):"""对偶模式的感知机训练方法train_data:训练数据集lr:学习率"""x_train = train_data[:,:-1]y_train = train_data[:,-1]num_samples, num_features = x_train.shapebeta = np.zeros((num_samples,))self.b = 0# 计算 Gram 矩阵gram = np.dot(x_train, x_train.T)while True:error_count = 0for i in range(num_samples):inner_product = gram[i]y_i = y_train[i]distance = y_i * (np.sum(beta * y_train * inner_product) + self.b)# 对于误分类点,修正 beta 和 偏置b,跳出本层循环,重新遍历数据计算,开始新的循环if distance <= 0:error_count += 1beta[i] = beta[i] + lrself.b = self.b + lr * y_ibreak # 数据没有误分类点,跳出 while 循环if error_count == 0:breakself.w = np.sum(beta * y_train * x_train.T, axis=1) # 计算w参数最终值print('w:{0}, b:{1}'.format(self.w, self.b))self.show_graph(train_data) # 展示图像def predict(self, sample):"""输入一个样本点,判断是-1类还是+1类sample:样本点"""output = self.w @ sample + self.breturn 1 if output >= 0 else -1def show_graph(self, train_data):"""把训练出来的超平面图像展示出来"""for sample in train_data:if sample[-1] == 1:plt.scatter(sample[0], sample[1],c='black',s=6)else:plt.scatter(sample[0], sample[1],c='red',s=6)x = np.linspace(0.,60.,200)y = -(self.w[0]*x + self.b) / self.w[1]plt.plot(x,y)plt.show()# 创建模型
model = Perception()
model.fit_raw_mod(dataset, lr=1)
w:[ 5.32765856 53.28693893], b:-1625.0

model = Perception()
model.fit_dual_mod(dataset, lr=1)
w:[ 5.00139101 51.70138198], b:-1580.0
model.predict(np.array([20,30]))
1
model.predict(np.array([50,50]))
1
这篇关于【技术干货】一文搞懂感知机算法:从理论到Python实战的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




