搞懂专题
【数据结构】——原来排序算法搞懂这些就行，轻松拿捏
前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
CSP-J基础之数学基础 初等数论 一篇搞懂(一)
文章目录 前言声明初等数论是什么初等数论历史1. **古代时期**2. **中世纪时期**3. **文艺复兴与近代**4. **现代时期** 整数的整除性约数什么样的整数除什么样的整数才能得到整数？条件：举例说明：一般化： 判断两个数能否被整除 因数与倍数质数与复合数使用开根号法判定质数哥德巴赫猜想最大公因数与辗转相除法计算最大公因数的常用方法：举几个例子：例子 1: 计算 12 和 18
CSP-J基础之数学基础 初等数论 一篇搞懂(二)
文章目录 前言算术基本定理简介什么是质数？举个简单例子：重要的结论：算术基本定理公式解释：举例： 算术基本定理的求法如何找出质因数：举个简单的例子： 重要的步骤：C++实现 同余举个例子：同余的性质简介1. 同余的自反性2. 同余的对称性3. 同余的传递性4. 同余的加法性质5. 同余的乘法性质 推论 总结 前言 在计算机科学和数学中，初等数论是一个重要的基础领域，涉及到整数
Flink: 两个递归彻底搞懂operator chain
《2021年最新版大数据面试题全面开启更新》 operator chain是指将满足一定条件的operator 链在一起，放在同一个task里面执行，是Flink任务优化的一种方式，在同一个task里面的operator的数据传输变成函数调用关系，这种方式减少数据传输过程。常见的chain例如：source->map->filter，这样的任务链可以chain在一起，那么其内部是如何决定
5分钟搞懂什么是Nginx?
一、What's nginx? 1、在服务器上可以组装网页并且可以响应(response)浏览器http请求(request)的软件。 2、支持负载均衡。 3、支持静态网页缓存 那么nginx可以扮演的角色为(每个角色可以单独为一台服务器)： 1、web server(组装网页）
学习笔记 | 一文搞懂MySQL体系架构！！！（day22）
本文章的内容会在后面文章中慢慢讲解，该文章主要给各位博友zaipin提供学习思路，也希望大家在评论区发言表述，觉得文章有不足指出也可点评，希望大家多多支持！！！ 目录 一、MySQL 1.1 数据库概述 1.2 数据库分类 1.2.1 关系型数据库 1.2.2 非关系型数据库 1.3 MySQL的安装 1.4 访问数据库服务器 1.5 SQL分类 1.6 MySQL注解
一文搞懂 JavaScript 模块化规范：CommonJS、AMD、ES6 Module
🔥 个人主页：空白诗 文章目录 一、为什么需要模块化？二、早期的模块化标准2.1 CommonJS 规范2.1.1 CommonJS 简介2.1.2 CommonJS 的特性2.1.3 CommonJS 的使用示例2.1.4 CommonJS 可能出现的问题 2.2. AMD 规范2.2.1 AMD 简介2.2.2 AMD 的特性2.2.3 AMD 的使用示例2.2.4 A
一文彻底搞懂大模型 - RAG（检索、增强、生成）
最近这一两周看到不少互联网公司都已经开始秋招提前批面试了。 不同以往的是，当前职场环境已不再是那个双向奔赴时代了。求职者在变多，HC 在变少，岗位要求还更高了。 最近，我们又陆续整理了很多大厂的面试题，帮助一些球友解惑答疑，分享技术面试中的那些弯弯绕绕。 《大模型面试宝典》(2024版) 正式发布 喜欢本文记得收藏、关注、点赞。文末技术交流 RAG（Retrieval-Augment
一篇搞懂classpath,resources
Classpath（类路径）在Java开发中是一个非常重要的概念，它指定了Java虚拟机（JVM）和Java编译器寻找类文件和包的位置。具体来说，Classpath告诉Java执行环境在哪些目录下可以找到所要执行的Java程序所需要的类或者包。这些目录可以是文件系统中的普通目录，也可以是包含编译后的Java类文件（.class文件）的JAR文件或ZIP文件。 Classpath的作用 类加载
一篇搞懂C++ STL 元组std::tuple
文章目录 前言什么是 `std::tuple`为什么要使用 `std::tuple``std::tuple` 的构造函数和操作函数1. 构造函数2. 操作函数 make_tuple函数`std::make_tuple` 的功能函数原型参数返回值使用示例`std::make_tuple` 的特点 示例代码总结 前言 在 C++ 中，元组（Tuple）是一种用于将多个不同类型的值
一篇搞懂C++ STL 存储重复键值对容器std::multimap
文章目录 前言为什么使用 `std::multimap``std::multimap` 与 `std::map` 的区别字符串图表示区别`std::multimap` 的构造函数和操作函数构造函数成员函数 示例代码 总结 前言 std::multimap 是 C++ STL 中的一个关联容器，用于存储键值对。与 std::map 不同，std::multimap 允许一个键关
【技术干货】一文搞懂感知机算法：从理论到Python实战
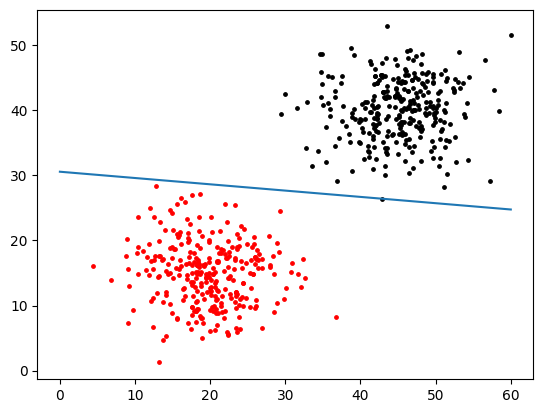
一 引言 在机器学习中，感知机（perceptron）是二分类的线性分类模型，属于监督学习算法。输入为实例的特征向量，输出为实例的类别（取+1和-1）。感知机对应于输入空间中将实例划分为两类的分离超平面。感知机旨在求出该超平面，为求得超平面导入了基于误分类的损失函数，利用梯度下降法对损失函数进行最优化（最优化）。感知机的学习算法具有简单而易于实现的优点，分为原始形式和对偶形式。感知机预测是用学习
一文彻底搞懂Fine-tuning - 预训练和微调（Pre-training vs Fine-tuning）
Pre-training vs Fine-tuning 预训练（Pre-training）是预先在大量数据上训练模型以学习通用特征，而微调（Fine-tuning）是在特定任务的小数据集上微调预训练模型以优化性能。 Pre-training vs Fine-tuning 为什么需要预训练？ 预训练是为了让模型在见到特定任务数据之前，先通过学习大量通用数据来捕获广泛有用的特征，从而
一文彻底搞懂Fine-tuning - 超参数（Hyperparameter）
Hyperparameter 超参数（Hyperparameter）， 是机器学习算法中的调优参数，用于控制模型的学习过程和结构。与模型参数（Model Parameter）不同，模型参数是在训练过程中通过数据学习得到的，而超参数是在训练之前由开发者或实践者直接设定的，并且在训练过程中保持不变。 Hyperparameter vs Model Parameter 超参数是机器学习算法
神经网络算法 - 一文搞懂Loss Function（损失函数）
本文将从损失函数的本质、损失函数的原理、损失函数的算法三个方面，带您一文搞懂损失函数 Loss Function 。。 损失函数 机器学习“三板斧”： 选择模型家族，定义损失函数量化预测误差， 通过优化算法找到最小化损失的最优模型参数。 机器学习 vs 人类学习 定义一个函数集合（模型选择） 目标：确定一个合适的假设空间或模型家族。 示例：线性回归、逻辑回归、神经网络、决
一文彻底搞懂CNN - 手写数字识别（LeNet-5）
LeNet-5是Yann LeCun在1998年设计的用于手写数字识别的卷积神经网络，是深度学习领域中的早期重要里程碑之一。它是第一个成功应用于手写数字识别的卷积神经网络，标志着深度学习在计算机视觉领域的初步应用。 MNIST数据集 LeNet-5以其简洁而有效的结构，成为了早期卷积神经网络中最具代表性之一。它成功奠定了卷积神经网络在计算机视觉领域的地位。 LeNet-5 一、CN
【超实用！】一文搞懂Transformer原理！✨
Hey小伙伴们！👋 今天要和大家分享一个超酷的技术点：Transformer模型的原理！如果你对深度学习和自然语言处理感兴趣，那么这篇文章绝对不容错过！👩💻✨ 📚 Transformer是什么？ Transformer是由Google的研究员们在2017年提出的一种全新的序列到序列模型。它彻底改变了自然语言处理领域，尤其是翻译、文本生成和问答等领域。相比于之前的RNN和LSTM模型，
一文彻底搞懂CNN - 卷积和池化（Convolution And Pooling）
Convolutional Neural Network CNN（卷积神经网络）最核心的两大操作就是卷积（Convolution）和池化（Pooling）。卷积用于特征提取，通过卷积核在输入数据上滑动计算加权和；池化用于特征降维，通过聚合统计池化窗口内的元素来减少数据空间大小。 Convolution And Pooling 一、_卷积（Convolution） 卷积（Convol
一文搞懂aPaaS与iPaaS（附低代码平台研究报告）
一、aPaaS（应用程序平台即服务） aPaaS，全称Application Platform as a Service，即应用程序平台即服务，是一种基于PaaS（平台即服务）的云服务模型。它为软件应用程序的开发和运行提供了一个全面的环境，支持应用程序在云端的开发、部署和运行。 1、功能特点： 快速开发环境：aPaaS平台提供了快速开发的环境，使用户能够在几个小时内完成应用的开发、测试、部署
神经网络算法 - 一文搞懂Gradient Descent（梯度下降）
本文将从梯度下降的本质、梯度下降的原理、梯度下降的算法 三个方面，带您一文搞懂梯度下降 Gradient Descent | GD。 梯度下降 机器学习“三板斧”：选择模型家族，定义损失函数量化预测误差，通过优化算法找到最小化损失的最优模型参数。 机器学习 vs 人类学习 定义一个函数集合（模型选择） 目标：确定一个合适的假设空间或模型家族。 示例：线性回归、逻辑回归、神
【面向对象】06一文搞懂抽象和接口 类与类之间的关系 抽象类与接口的相同点与不同点(多代码)
文章目录 一、抽象1.抽象类与抽象方法2.抽象方法的特点 二、接口1.interface2.接口特征 三、类与类之间的关系四、抽象类 VS 接口相同点不同点 一、抽象 1.抽象类与抽象方法 // 抽象类public abstract class Pet {// 抽象方法public abstract void toHospital() ;} 2.抽象方法的特点 修
一文彻底搞懂Transformer - Why Self-Attention（为什么是自注意力）
Transformer 使用自注意力（Self-Attention）机制在序列处理任务中，特别是自然语言处理（NLP）领域，变得越来越流行，主要是因为它在计算复杂度、并行化能力、长距离依赖的建模能力 等多个关键方面相较于传统的循环神经网络（RNNs）和卷积神经网络（CNNs）具有显著的优势。 一、计算复杂度 计算复杂度： 自注意力机制尽管计算复杂度为O(n^2)，但通过高度优化的矩阵运算库
神经网络算法 - 一文搞懂Embedding（嵌入）
本文将从Embedding的本质、Embedding的原理、Embedding的应用三个方面，带您一文搞懂Embedding（嵌入） “Embedding”在字面上的翻译是“嵌入”，但在机器学习和自然语言处理的上下文中，我们更倾向于将其理解为一种“向量化”或“向量表示”的技术，这有助于更准确地描述其在这些领域中的应用和作用。 1. 机器学习中的Embedding 原理：将离散数据映
一文彻底搞懂Transformer - 总体架构，零基础入门到精通，收藏这一篇就够了
Transformer 一、RNN编码器-解码器架构**** ********序列到序列模型（Seq2Seq）：Seq2Seq模型的目标是将一个输入序列转换成另一个输出序列，这在多种应用中都具有广泛的实用价值，例如语言建模、机器翻译、对话生成等。 Seq2Seq **RNN编码器-解码器架构：**Transformer出来之前，主流的序列转换模型都基于复杂的循环神经网络（RNN），