奇异专题
特征值分解(EVD)和奇异值分解(SVD)—应用于图片压缩
特征值分解(EVD)和奇异值分解(SVD)—应用于图片压缩 目录 前言 一、特征值分解 二、应用特征值分解对图片进行压缩 三、矩阵的奇异值分解 四、应用奇异值分解对图片进行压缩 五、MATLAB仿真代码 前言 学习了特征值分解和奇异值分解相关知识,发现其可以用于图片压缩,但网上没有找到相应代码,本文在学习了之后编写出了图片压缩的代码,发现奇异值分
基于Python的机器学习系列(23):奇异值分解(SVD)
在本篇中,我们将介绍如何利用奇异值分解(SVD)进行降维。SVD 是一种强大的矩阵分解方法,可以帮助我们提取数据中的重要特征,广泛应用于数据分析、图像处理等领域。 问题定义 在数据分析中,特别是当数据维度很高时,我们经常需要减少数据的维度以便于处理和可视化。奇异值分解(SVD)提供了一种有效的方法来实现这一目标。SVD 通过将原始数据矩阵分解成三个矩阵的乘积,从
奇异递归模板模式(Curiously Recurring Template Pattern)
奇异递归模板模式(Curiously Recurring Template Pattern) - 知乎 (zhihu.com) 本文来自上面的文章!!!本菜鸡学习和记录一下。 CRTP是C++模板编程时的一种惯用法:把派生类作为基类的模板参数。 1.静态多态 #include <iostream>using namespace std;template <typename Child>
特征值分解(EVD)和奇异值分解(SVD)
两篇博文,写得很好: http://blog.sina.com.cn/s/blog_3f738ee00102val0.html http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
PCA降维奇异值分解SVD
PCA降维 涉及高维数据的问题容易陷入维数灾难,随着数据集维数的增加,算法学习所需的样本数量呈指数级增加,且需要更多的内存和处理能力,消耗资源。主成分分析也称为K-L变换,常用于高位数据预处理和可视化。PCA可以把可能具有相关性的高维变量合成线性无关的低维变量,称为主成分。原理就是PCA将高维具有相关性的数据进行线性变换映射到一个低维子空间,尽可能多的保留更多变量(代表原特征),降维成一个线性无
主成分分析与奇异值分解
机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用 版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gmail.com。也可以加我的微博: @leftnoteasy 转载https://www.cnblogs.com/Left
奇异递归Template有啥奇的?
如果一个模版看起来很头痛,那么大概率这种模版是用来炫技,没啥用的,但是CRTP这个模版,虽然看起来头大,但是却经常被端上桌~ 奇异递归模板模式(Curiously Recurring Template Pattern, CRTP)是一种 C++ 模板编程技巧,用于实现静态多态。这种模式利用模板递归来允许一个类继承自一个模板类,其中模板参数是该类自身。这种模式可以用于各种用途,包括实现类型安全的单
奇异值与潜在语义索引LSI
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html 潜在语义索引(Latent Semantic Indexing)与PCA不太一样,至少不是实现了SVD就可以直接用的,不过LSI也是一个严重依赖于SVD的算法,之前吴军老师在矩阵计算与文本处理中的分类问题中谈到: “三个矩阵有
【转】奇异值分解(SVD)原理详解及推导
本文转载于陈靖博客http://blog.csdn.net/zhongkejingwang/article/details/43053513 在网上看到有很多文章介绍SVD的,讲的也都不错,但是感觉还是有需要补充的,特别是关于矩阵和映射之间的对应关系。前段时间看了国外的一篇文章,叫A Singularly Valuable Decomposition The SVD of a Ma
奇异值分解简介:从原理到基础机器学习应用
矩阵分解在机器学习应用中的重要性无需多言。本文对适用范围很广的奇异值分解方法进行了介绍,并通过代码演示说明了其工作方式、计算方法及其常见的几种基础应用。 矩阵分解也叫矩阵因子分解,涉及到用给定矩阵的组成元素描述该矩阵。 奇异值分解(SVD)可能是最著名和使用最广泛的矩阵分解方法。所有矩阵都有一种 SVD 方法,这使得其比特征分解(eigendecomposition)等其它方法更加稳定。因
【图像隐藏】基于奇异值分解SVD实现数字水印嵌入提取,相关系数NC附Matlab代码
以下是使用奇异值分解(SVD)实现数字水印嵌入和提取的相关系数(NC)的Matlab代码示例: matlab % 数字水印嵌入 function watermarked_image = embed_watermark(original_image, watermark, strength) % 将原始图像进行SVD分解 [U, S, V] = svd(double(original_image
基于机器学习和奇异值分解SVD的电池剩余使用寿命预测(Python)
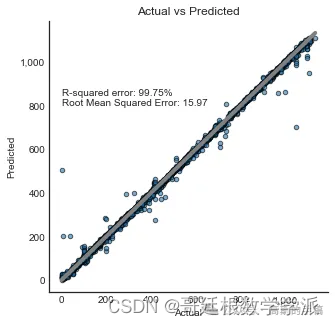
采用k-最近邻KNN和随机森林算法建立预测模型。 import pandas as pdfrom sklearn.model_selection import train_test_splitfrom sklearn.svm import SVC # Support Vector Classifierfrom sklearn.preprocessing import StandardSc
特征值分解、奇异值分解、PCA概念整理
特征值分解、奇异值分解、PCA概念整理 一、特征值与特征向量的几何意义 1. 矩阵乘法 在介绍特征值与特征向量的几何意义之前,先介绍矩阵乘法的几何意义。 矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度的新向量。在这个变化过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某些向量只发生伸缩变换,不产生旋转效果,那么这些向量就称为这
【机器学习】必会降维算法之:奇异值分解(SVD)
奇异值分解(SVD) 1、引言2、奇异值分解(SVD)2.1 定义2.2 应用场景2.3 核心原理2.4 算法公式2.5 代码示例 3、总结 1、引言 一转眼, 小屌丝:鱼哥,就要到每年最开心的节日了:六一儿童节。 小鱼:你有啥想法? 小屌丝:想法没有,玩的地方倒是想 小鱼:拉倒吧, 我可不去 小屌丝:确定? 小鱼:看情况。 小屌丝:嘿嘿, 难得过节日,我们也得放松一下 小鱼:正
C++中的奇异递归模板CRTP
CRTP 的基本概念: CRTP 的核心思想是:一个基类(Base)将派生类(Derived)作为模板参数。在基类中,可以定义一些依赖于派生类行为的成员函数。这样可以在编译期间实现类似于动态多态性(即虚函数机制),但没有运行时开销。 基本示例: #include <iostream>// 基类模板template <typename Derived>class B
奇异值分解的几何原理
转载地址http://blog.sciencenet.cn/home.php?mod=space&uid=696950&do=blog&quickforward=1&id=699380
【设计模式】JAVA Design Patterns——Curiously Recurring Template Pattern(奇异递归模板模式)
🔍目的 允许派生组件从与派生类型兼容的基本组件继承某些功能。 🔍解释 真实世界例子 对于正在策划赛事的综合格斗推广活动来说,确保在相同重量级的运动员之间组织比赛至关重要。这样可以防止体型明显不同的拳手之间的不匹配,例如重量级拳手与雏量级拳手的对决。 通俗描述 使类型中的某些方法接受特定于其子类型的参数。 维基百科 奇异递归模板模式(curiously
数据可视化(十二):Pandas太阳黑子数据、图像处理——离散极值、核密度、拟合曲线、奇异值分解等高级操作
Tips:"分享是快乐的源泉💧,在我的博客里,不仅有知识的海洋🌊,还有满满的正能量加持💪,快来和我一起分享这份快乐吧😊! 喜欢我的博客的话,记得点个红心❤️和小关小注哦!您的支持是我创作的动力!数据源存放在我的资源下载区啦! 数据可视化(十二):Pandas太阳黑子数据、图像处理——离散极值、核密度、拟合曲线、奇异值分解等高级操作 目录 数据可视化(十二):Pandas太
特征值分解、奇异值分解(SVD)、主成分分析(PCA)
1、 特征值分解(SVD): A=Q∑Q−1 A=Q\sum Q^{-1} Q= [v1,v2,...] [v_1,v_2,...] ∑=⎡⎣⎢λ1000λ20
AI学习指南线性代数篇-奇异值分解
AI学习指南线性代数篇-奇异值分解 一、概述 在人工智能领域,线性代数是一项非常重要的基础知识,而奇异值分解(Singular Value Decomposition, SVD)作为线性代数中的一种重要工具,被广泛应用于机器学习、数据科学等领域。本文将深入探讨奇异值分解的相关概念、使用场景、定义、意义和公式讲解。 二、奇异值分解在AI中的使用场景 奇异值分解在人工智能领域被广泛应用,特别是
关于奇异值分解SVD很好的解释
上一次写了关于 PCA与LDA的文章,PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值分解去实现的。在上篇文章中便是基于特征值分解的一种解释。特征值和奇异值在大部分人的印象中,往往是停留在纯粹的数学计算中。而且线性代数或者矩阵论里面,也很少讲任何跟特征值与奇异值有关的应用背景。奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的
【推荐架构day7】爱奇异推荐算法的演进之路
在当前这个移动互联网时代,除了专业内容的丰富,UGC内容更是爆发式发展,每个用户既是内容的消费者,也成为了内容的创造者。这些海量的内容在满足了我们需求的同时,也使我们寻找所需内容更加困难,在这种情况下个性化推荐应运而生。 个性化推荐是在大数据分析和人工智能技术的基础上,通过研究用户的兴趣偏好,进行个性化计算,从而给用户提供高质量的个性化内容,解决信息过载的问题,更好的满足用户的需求。 爱
Singular Value Decomposition:奇异值分解(降维)
SVD 降维 相似度计算: 1.欧式距离 向量的范数2 2.皮尔逊相关系数 cov(X,Y)varxvary c o v ( X , Y ) v a r x v a r y \frac{cov_{(X,Y)}}{var{x} var{y}} 均值意义:样本集合的中间点 方差意义: 样本点的离散程度 协方差意义: 度量两个随机变量关系的统计量 度量各个维度偏离其均值的程度 协方差计
【图像隐写】基于matlab离散小波变换(DWT)与奇异值分解(SVD)数字水印(含PSNR、NC)【含Matlab源码 521期】
✅博主简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,Matlab项目合作可私信。 🍎个人主页:海神之光 🏆代码获取方式: 海神之光Matlab王者学习之路—代码获取方式 ⛳️座右铭:行百里者,半于九十。 更多Matlab仿真内容点击👇 Matlab图像处理(进阶版) 路径规划(Matlab) 神经网络预测与分类(Matlab) 优化求解(Matlab) 语音处理(Matlab