周期性专题
周期性清除Spark Streaming流状态的方法
在Spark Streaming程序中，我们经常需要使用有状态的流来统计一些累积性的指标，比如各个商品的PV。简单的代码描述如下，使用mapWithState()算子： 现在的问题是，PV并不是一直累加的，而是每天归零，重新统计数据。要达到在凌晨0点清除状态的目的，有以下两种方法。 编写脚本重启Streaming程序 用crontab、Azkaban等在凌晨0点调度执行下面的Shell脚本
实时Linux性能监控脚本：周期性自动统计CPU、内存和IO使用情况
Linux Shell 脚本实现每3秒钟统计 CPU 占用率、内存空间、IO、单核 CPU 占用率、CPU 占用率最高的前10个应用进程以及指定目录 /opt 的磁盘空间变化。 Shell脚本 #!/bin/bash# 输出文件路径OUTPUT_FILE="/var/log/system_monitor.log"# 创建/清空输出文件> $OUTPUT_FILE# 获取 CPU 核心数量
【watch】周期性的执行指定命令，并以全屏方式显示结果
【watch】周期性的执行指定命令，并以全屏方式显示结果 例如： watch 'cat /etc/passwd' //则每隔两秒执行一次cat /etc/passwd命令 参数 【-n #】:指定周期长度，单位为秒，默认为2 格式：watch -n # 'COMMAND'
【深度学习】如何理解 Transformer 位置编码：每个位置的编码真的都是唯一的吗？还是周期性的？
文章目录 理解 Transformer 位置编码：每个位置的编码真的都是唯一的吗？位置编码的基本原理位置编码真的独一无二吗？周期性与最小公倍数 如何计算周期最小公倍数的计算实际中的周期重复实际应用中的位置编码总结 理解 Transformer 位置编码：每个位置的编码真的都是唯一的吗？ 在深入学习自然语言处理（NLP）模型的过程中，Transformer 模型以其强大的性能
3.6. 马氏链-极限分布与周期性
极限分布与周期性 1. 返回次数收敛性1.1. 时间 n n n前访问 y y y次数的极限分布1.2. 时间 n n n前访问 z z z的次数-比率极限定理 2. p n ( x , y ) p_n(x,y) pn(x,y)的极限分布(非周期情形)2.1. 周期的定义和性质2.2. 不可约+非周期+有平稳分布 → ρ n ( x , y ) \rightarrow \rho^n(x
crond 周期性计划使用方法
一、crond简介 crond是linux下用来周期性的执行某种任务或等待处理某些事件的一个守护进程，与windows下的计划任务类似，当安装完成操作系统后，默认会安装此服务工具，并且会自动启动crond进程，crond进程每分钟会定期检查是否有要执行的任务，如果有要执行的任务，则自动执行该任务。 Linux下的任务调度分为两类，系统任务调度和用户任务调度。 系统任务调度：系统周期性所要执行
椭圆轨道的周期性运动轨道
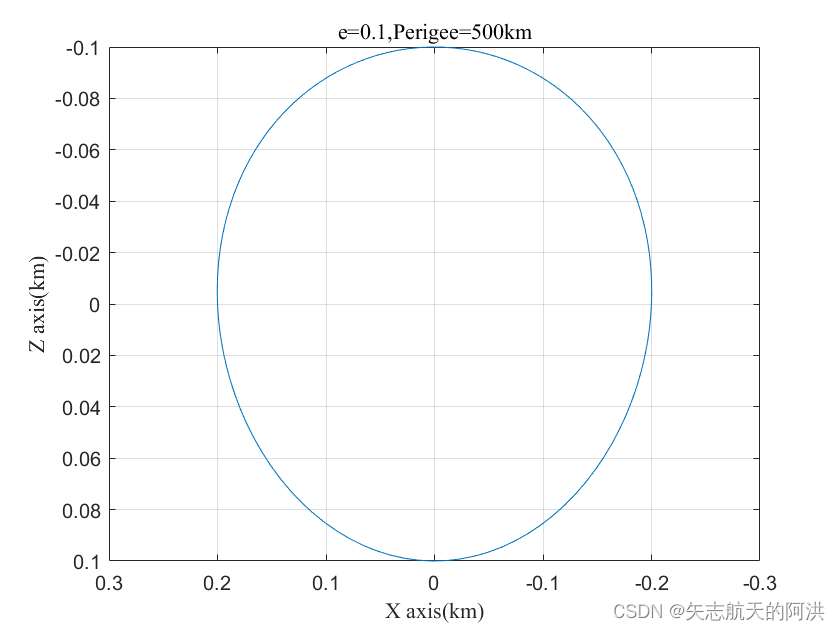
一、背景介绍 本节将从轨道六根数的角度，探究目标星为椭圆轨道，追踪星周期性环绕目标的必要条件。根据航天动力学的原理，对于一个椭圆轨道，其轨道能量为 对于能够不产生漂移的情况，绕飞编队的能量。对于追踪星到目标星的能量差，可以写 因此，对于零能量差的形式可以写为 通过使用下列离心率的关系 式中：为轨道近地点位置，所以离心率偏差可以写为近地点角的偏差，即 通过对上式修改，
Linux CFS调度器之周期性调度器scheduler_tick函数
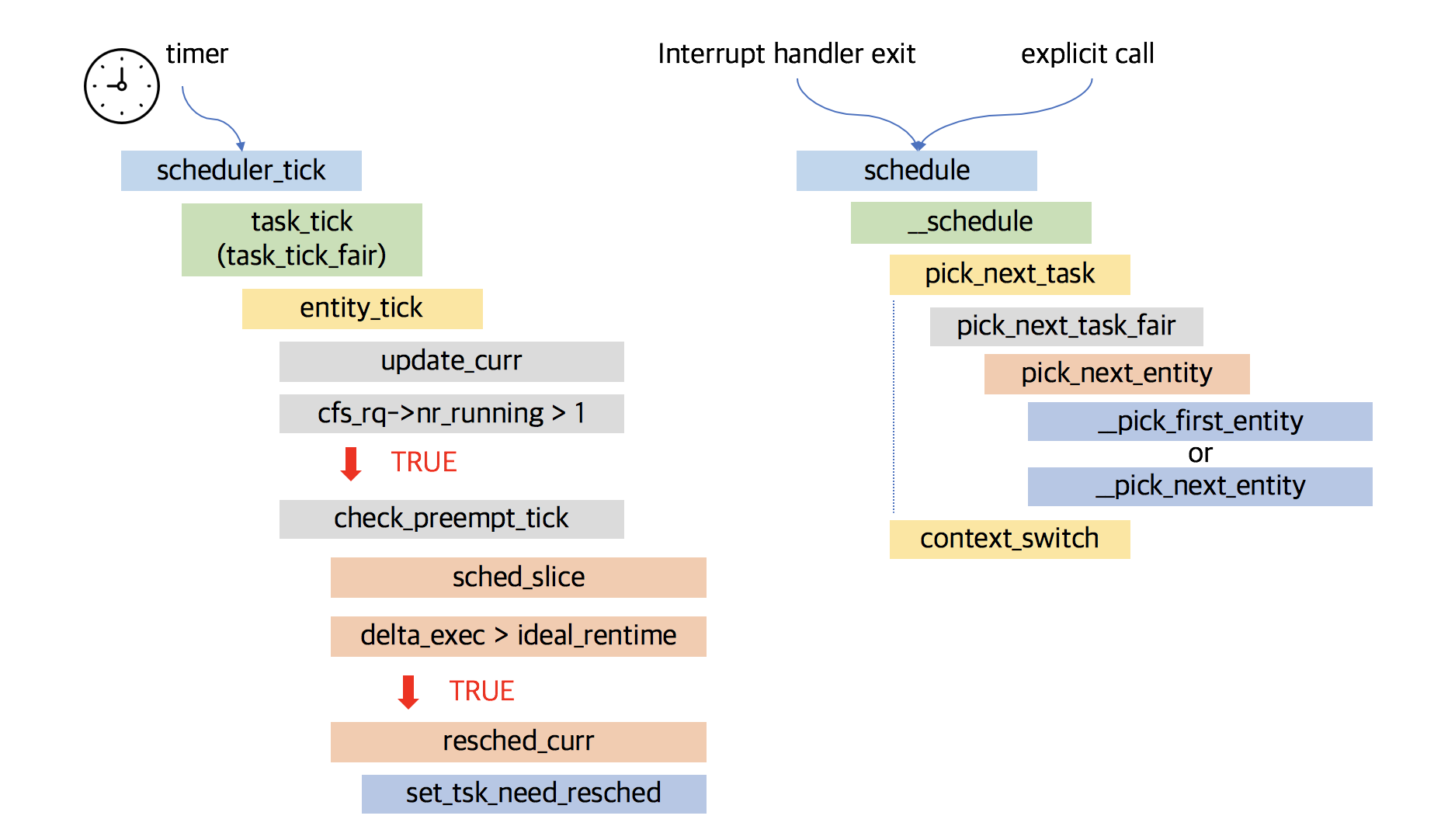
文章目录 前言一、简介二、源码分析2.1 scheduler_tick2.2 task_tick2.3 entity_tick2.4 check_preempt_tick2.5 resched_curr 参考资料 前言 Linux内核调度器主要是主调度器和周期性调度器，主调度器请参考：Linux 进程调度之schdule主调度器 一、简介 每当定时器中断发生时，都会调用定时器
ScheduledThreadPoolExecutor 周期性执行任务的线程池作用，基本使用，使用场景
ScheduledThreadPoolExecutor是Java并发编程中一个非常实用的类，它是java.util.concurrent包下的一个线程池实现，专为定时或周期性任务执行而设计。它提供了灵活且强大的定时任务调度功能，相比传统的Timer类，它具备更好的并发控制能力和错误处理机制。 作用 定时执行：可以安排任务在未来的某个特定时间点执行一次。周期性执行：支持任务按照固定的延迟时间重复
OpenCV的周期性噪声去除滤波器(70)
返回:OpenCV系列文章目录（持续更新中......） 上一篇:OpenCV如何通过梯度结构张量进行各向异性图像分割(69) 下一篇 :OpenCV如何为我们的应用程序添加跟踪栏(71) 目录 目标 理论 如何消除傅里叶域中的周期性噪声？ 源代码 解释 结果 目标 在本教程中，您将学习： 如何消除傅里叶域中的周期性噪声 理论 注意 解释基于该书[108]。此
UE5 GAS开发P40 周期性效果,持续治疗
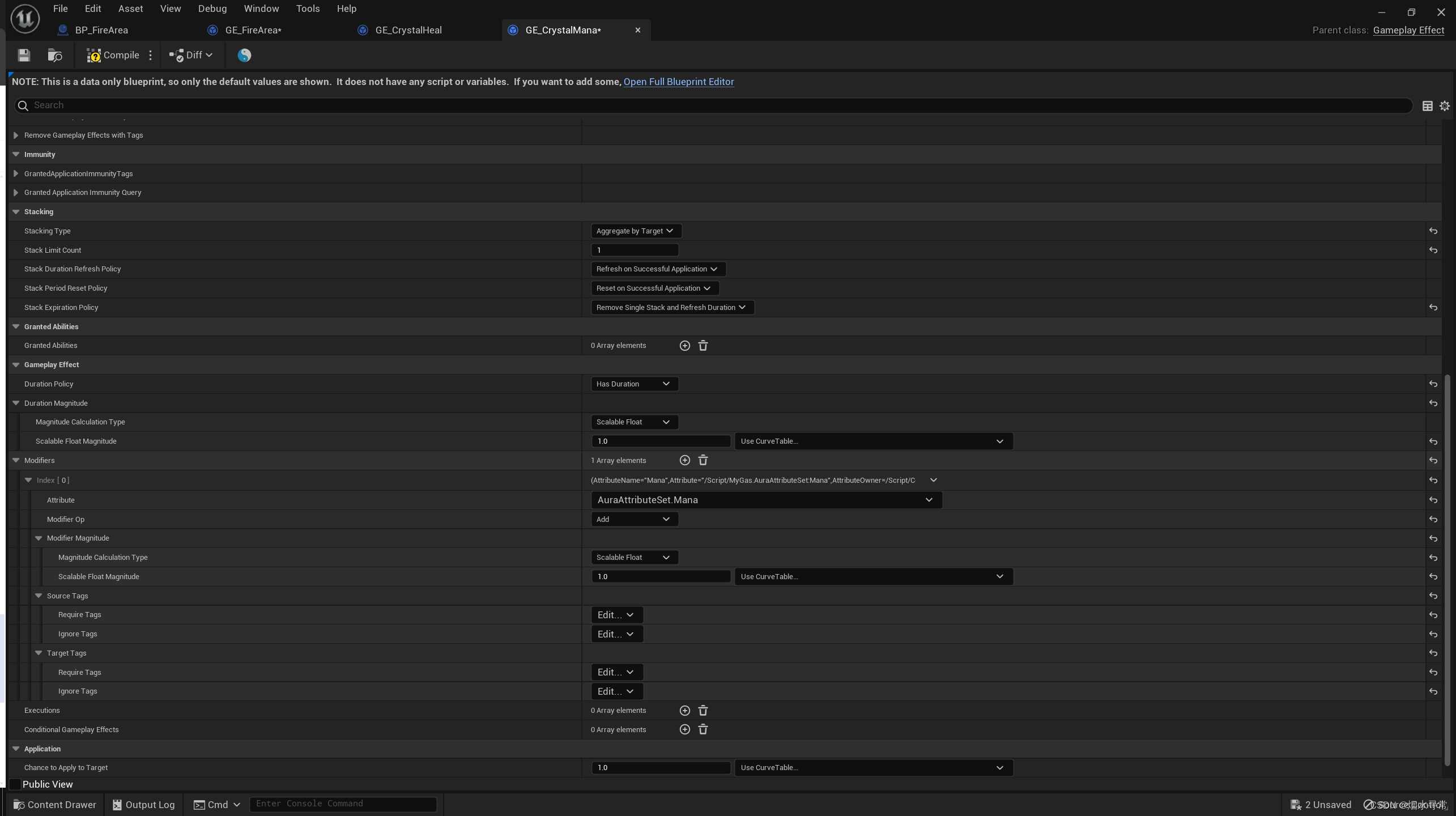
Periodic Gameplay Effects周期性的游戏效果 它们在一段时间内以固定的间隔重复应用到目标上。这种效果通常用于表示持续性伤害、治疗或其他影响，例如中毒、灼烧或回复效果。 修改GE_CrystalHeal,在Period改为每0.1秒执行一次 假如同时有三个持续时间在进行,那么这个时候蓝量就会超出Max的范围.这个时候就要引入Stacking(堆栈)的概念
数学分析复习：三角函数的周期性
文章目录 三角函数的周期性 本篇文章适合个人复习翻阅，不建议新手入门使用 三角函数的周期性 本节的主题是研究三角函数的周期性，我们之前已经解析地定义三角函数为 cos x = ∑ k = 0 ∞ ( − 1 ) k x 2 k ( 2 k ) ! , sin x = ∑ k = 0 ∞ ( − 1 ) k x 2 k + 1 ( 2 k + 1 ) ! \cos
基于Linux定时任务实现的MySQL周期性备份
1、创建备份目录 sudo mkdir -p /var/backups/mysql/database_name 2、创建备份脚本 sudo touch /var/backups/mysql/mysqldump.sh# 用VIM编辑脚本文件，写入备份命令sudo vim /var/backups/mysql/mysqldump.sh# 内如如下#!/bin/bashmysqldu
![【洛谷 P8700】[蓝桥杯 2019 国 B] 解谜游戏 题解（字符串+映射+周期性）](https://img-blog.csdnimg.cn/img_convert/c1733f6b4f09b37cf356fb26028fffe0.png)
【洛谷 P8700】[蓝桥杯 2019 国 B] 解谜游戏 题解（字符串+映射+周期性）
[蓝桥杯 2019 国 B] 解谜游戏 题目背景 题目描述 小明正在玩一款解谜游戏。谜题由 24 24 24 根塑料棒组成，其中黄色塑料棒 4 4 4 根，红色 8 8 8 根，绿色 12 12 12 根 (后面用 Y 表示黄色、R 表示红色、G 表示绿色)。初始时这些塑料棒排成三圈，如上图所示，外圈 12 12 12 根，中圈 8 8 8 根，内圈 4 4 4 根。 小
esp32蜂鸣器进行周期性鸣叫
板载蜂鸣器 无源蜂鸣器是一种简单的声音发生器，它通常由振片和共振腔组成。无源蜂鸣器不具备驱动电路，因此需要外部的电子设备来产生声音。当给无源蜂鸣器施加交变电压时，振片会振动并产生声音。无源蜂鸣器的工作频率由施加的电压频率决定。在使用无源蜂鸣器时，我们需要通过控制电压的频率和占空比来控制蜂鸣器的声音。通过改变交变电压的频率和占空比，我们可以产生不同的音调和音乐效果。无源蜂鸣器发出声音需要让io口输
每日shell脚本之自动化备份数据库周期性灾备
每日shell脚本之自动化备份数据库周期性灾备 使用本脚本前在服务器安装 物理备份工具-xtrabackup #!/usr/bin/bash #CSDN :M乔木 #Email:2776617348@qq.com #解释器:这是一个shell脚本 #数据库用户密码user=数据库用户passwd=数据库密码#检查备份情况bm(){if [ $?
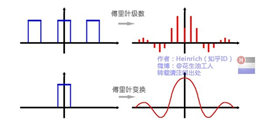
音频信号周期性的判断及周期测量
对于一般的周期信号 ，将 展开成傅里叶级数得： f ( t ) = ∑ n = − ∞ ∞ F n e j n w 1 t f(t)=\sum\limits_{n=-\infty }^{\infty }{{{F}_{n}}{{e}^{jn{{w}_{1}}t}}} f(t)=n=−∞∑∞Fnejnw1t 将上式两边取傅里叶变换得： F [ f ( t ) ] = 2 π ∑ n =
解决crond周期性调度重复执行问题
crond是linux下用来周期性执行某种任务或等待处理某些事件的一个守护进程，crond进程每分钟会定期检查是否有要执行的任务，如果有，就会自动执行该任务。 例如： */1 * * * * cd /home/nxuser/sdqx&&./run.sh >> run.log 2>&1 但如果周期内未执行完，导致重复执行，如何解决？ 利用 linux flock 锁机制： 格式：
利用task实现周期性任务
通过run函数返回值〉0 来实现周期性任务，返回值以毫秒为单位，将插入到taskthread中的OSHeap fHeap中。 class RTCPTask:public Task{public:RTCPTask(void);~RTCPTask(void);SInt64 Run();}; #include "RTCPTask
【零基础学习CAPL】——CAN报文的发送（按下按钮同时周期性发送）
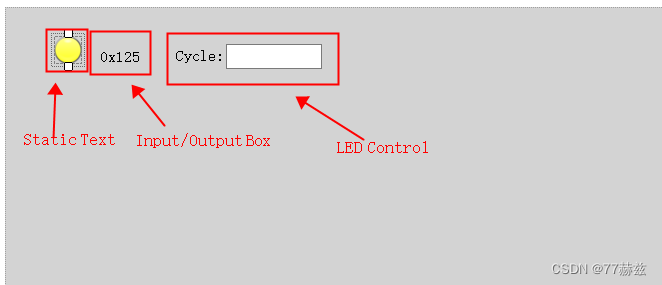
🙋♂️【零基础学习CAPL】系列💁♂️点击跳转 文章目录 1.概述2.面板创建3.系统变量创建4.CAPL实现4.1.函数展示4.2.全量报文展示 5.效果 1.概述 本章主要介绍使用CAPL和Panel在按下按钮时发送周期性CAN报文。 本章主要在“【零基础学习CAPL】——CAN报文的发送（配合Panel面板单次发送）”基础上进一步进行讲解。 2.面板创建 在面板
MATLAB - 仿真单摆的周期性摆动
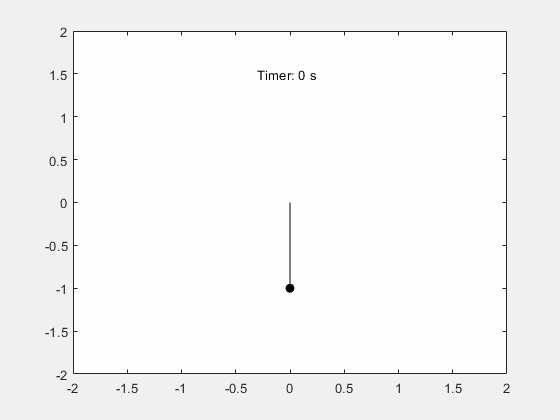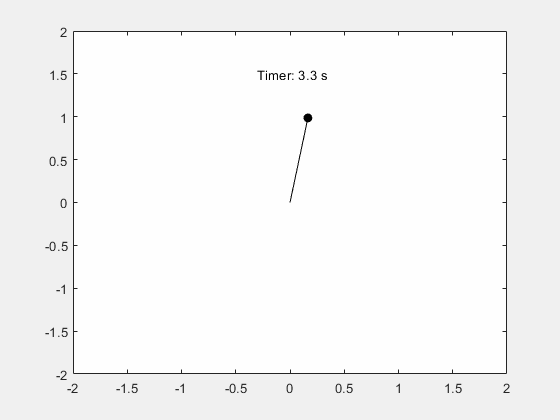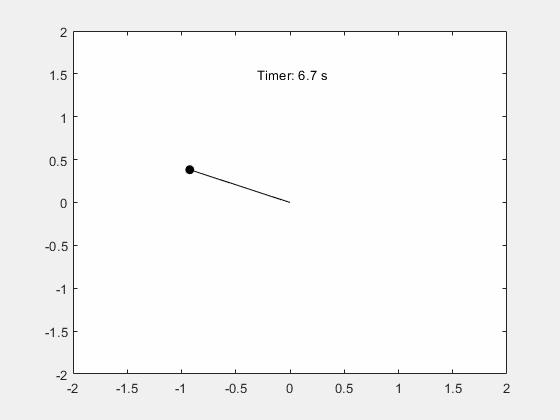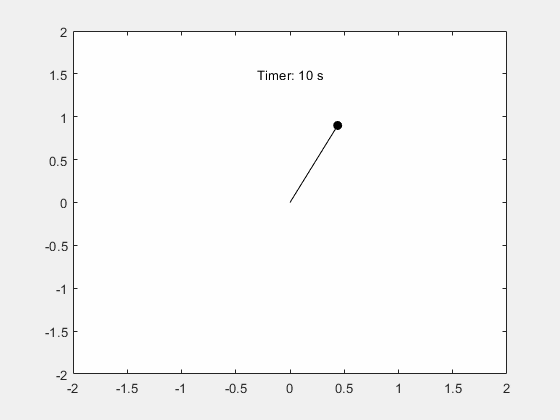
系列文章目录 前言 本例演示如何使用 Symbolic Math Toolbox™ 模拟单摆的运动。推导摆的运动方程，然后对小角度进行分析求解，对任意角度进行数值求解。 一、步骤 1：推导运动方程 摆是一个遵循微分方程的简单机械系统。摆最初静止在垂直位置。当摆移动一个角度 θ 并释放时，重力将其拉回静止位置。它的动量会使它过冲并到达 -θ 角（如果没有摩擦力），以此类推
BIEE周期性认证失败故障解决
环境： 操作系统：win 7 x64 BIEE版本： 11.1.1.7 RCU数据库：Oracle 11.2.0.1 现象： BIEE启动正常运行一段时间后，出现无法登录analytics应用的情况。 重启BIEE之后，analytics可用，但运行一段时间后再次出现无法登录的错误。 此现象周期性发生。 检查domain日志
普通Java工程利用注解Spring做周期性任务调度框架搭建
需求： 利用注解Spring做周期任务执行操作，这样如果利用spring的task去操作那么会非常简单。 实现： lib依赖： <dependency><groupId>org.springframework</groupId><artifactId>spring-core</artifactId><version>3.2.0.RELEASE</version></dependency><d
周期性定时事件的处理
文章目录 1 周期性定时事件的处理1.1 定时要求1.2 周期性触发软定时器 1 周期性定时事件的处理 1.1 定时要求 1.2 周期性触发软定时器 代码如下： /*** @brief tOS应用示例* @details* @author 01课堂 李述铜 http://01ketang.cc* @date 2017-06-01* @version 1.0* @
一个H3C交换机周期性断网并自动恢复的排查案例
一个朋友发我一个H3C日志，这个交换机是汇聚层交换机，1和2口是trunk口，其它接口是access接口，17-21口据说接的都是监控、终端。日志里面看到大量的拓朴改变，好几个网口up、down的日志，怀疑是环路，排除了本机环路后，我让他对access端口开启了端口保护，然后就排查两个trunk口的问题 我怀疑两个trunk口，可能一个是上联到核心，一个是下联
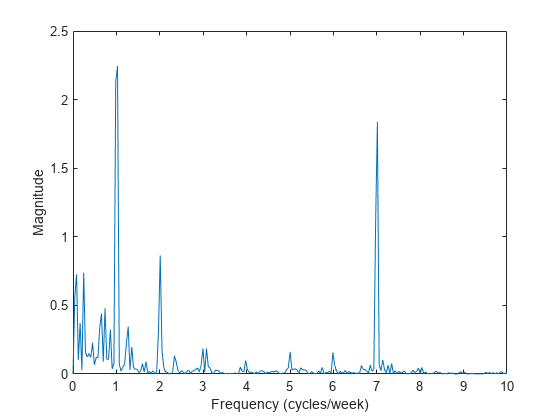
使用频率分析求周期性
通常很难通过观察时间测量值来表征数据中的振荡行为。频谱分析有助于确定信号是否为周期性信号并测量不同周期。 办公楼内的温度计每半小时测量一次室内温度，持续四个月。加载数据并对其绘图。将温度转换为摄氏度。测量时间以周为单位。因此，采样率为 2 次测量/小时 × 24 小时/天 × 7 天/周 = 336 次测量/周。 load officetemptempC = (