椭圆轨道的周期性运动轨道

本文主要是介绍椭圆轨道的周期性运动轨道，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、背景介绍

本节将从轨道六根数的角度，探究目标星为椭圆轨道，追踪星周期性环绕目标的必要条件。根据航天动力学的原理，对于一个椭圆轨道，其轨道能量为

$\varepsilon=-(\mu/2a)$

对于能够不产生漂移的情况，绕飞编队的能量 $\varepsilon_{i}$ 。对于追踪星到目标星的能量差，可以写

$\delta\varepsilon=\varepsilon_{i}-\varepsilon=(V^{2}_{pi}/2-\mu/r_{Pi})-(V_{p}^2-\mu/r_p)$

因此，对于零能量差的形式可以写为

$V_{Pi}^{2}-V_{P}^{2}=2\mu(\frac{r_p-r_{pi}}{r_p r_{pi}})$

通过使用下列离心率的关系

$e=1-\frac{r_p}{a}$

式中： $r_p$ 为轨道近地点位置，所以离心率偏差 $\delta e_{i}$ 可以写为近地点角的偏差 $\delta r_{i}$ ，即

$\delta e_{i}=e_i-e=(1-\frac{r_{pi}}{a})-(1-\frac{r_p}{a})=-(\delta r_i/a)$

通过对上式修改，可以得到

$\frac{V_{pi}}{V_p}=\sqrt{1-\frac{2\mu}{V_p^{2}}[\frac{\delta r_i}{a^2(1-e)(1-e_i)}]}=\sqrt{1+\frac{2\mu}{aV_p^{2}}[\frac{\delta e_{i}}{(1-e)(1-e_i)}]}$

上述是微分能量的精确表达式，注意到 $V_{pi}$ 和 $e_i$ 存在复杂的耦合关系。最后的表达式近似表达为

$\frac{V_{pi}}{V_p}\approx1+\frac{\mu}{aV_p^2}[\frac{\delta e_i}{(1-e)^2}]$

假设 $\left | \delta e_i \right | \ll1$ 且 $V_p\geq V_{cs}$ 。在这里 $V_{cs}=\sqrt{\frac{\mu}{a}}$ 是给定半长轴圆轨道的速度

$V_p^2=\frac{\mu(1+e)}{a(1-e)}$

所以 $V_p\geq V_{cs}$ ，对于任意 $0\leq e<1$ ，等式被写为

$\delta V_{pi}\approx\frac{\mu}{aV_p}[\frac{\delta e_i}{(1-e)^2}]=-\frac{\mu}{a^2V_p}[\frac{\delta r_i}{(1-e)^2}]=-\frac{n\delta r_{i}}{(1-e)^{\frac{3}{2}}(1+e)^{\frac{1}{2}}}$

根据运动学关系 $\delta \boldsymbol{V}_{\textup{abs}}=\delta \boldsymbol{V}_{\textup{rel}}+\boldsymbol{\omega} \times \delta\boldsymbol{ r}$ ，在线性化的框架中，对于给定的几何形状，可以计算按到底层中心的参考的微分速度，在绝对惯性坐标系下，目标星在近地点的角速度

$\omega =\dot{\theta }(0)=\frac{n(1+e)}{(1-e)^{\frac{3}{2}}(1+e)^{\frac{1}{2}}}$

在目标星的相对坐标系，追踪星的速度可以写为

$\delta V_{P_{\textup{abs}}}=-\frac{n(2+e)\delta r_i}{(1-e)^{\frac{3}{2}}(1+e)^{\frac{1}{2}}}$

在VVLH坐标系下，初始条件满足关系式即为

$\frac{z(0)}{x^{'}(0)}=\frac{n(2+e)}{(1+e)^{\frac{1}{2}}(1-e)^{\frac{3}{2}}}$

二、STK仿真验证

下面这段代码，在之前TH方程的基础上，在STK添加VVLH报表后，进行仿真得到的结果

% 使用STK验证VVLH坐标系
clc;clear
uiApplication = actxGetRunningServer('STK12.application');
root = uiApplication.Personality2;
checkempty = root.Children.Count;
if checkempty ~= 0root.CurrentScenario.Unloadroot.CloseScenario;
end
root.NewScenario('VVLH');
StartTime = '26 Jan 2024 04:00:00.000';    % 场景开始时间
StopTime = '10 Feb 2024 04:00:00.000';     % 场景结束时间
root.ExecuteCommand(['SetAnalysisTimePeriod * "',StartTime,'" "',StopTime,'"']);
root.ExecuteCommand(' Animate * Reset');
SatName = 'Target';       %  SAR_   GX_   Sat_  GX_1_  SAR_1_
satellite = root.CurrentScenario.Children.New('eSatellite', SatName);
satellite.SetPropagatorType('ePropagatorAstrogator');   %  不设置的时候默认为二体模型  ePropagatorJ4Perturbation
satellite.Propagator;
Perigee=6378.137+500;
Ecc=0.1;
sma=Perigee/(1-Ecc);
Inc=30;
w=0;
RAAN=0;
TA=0;
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' SetValue MainSequence.SegmentList Initial_State Propagate']);
InitialState=satellite.Propagator.MainSequence.Item(0);
%% 初始化卫星参数
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' SetValue MainSequence.SegmentList.Initial_State.CoordinateType Modified Keplerian']);
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' SetValue MainSequence.SegmentList.Initial_State.InitialState.Epoch ',StartTime,' UTCG']);
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' SetValue MainSequence.SegmentList.Initial_State.InitialState.Keplerian.sma ',num2str(sma),' km']);
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' SetValue MainSequence.SegmentList.Initial_State.InitialState.Keplerian.ecc ',num2str(Ecc)]);
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' SetValue MainSequence.SegmentList.Initial_State.InitialState.Keplerian.inc ',num2str(Inc),' deg']);
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' SetValue MainSequence.SegmentList.Initial_State.InitialState.Keplerian.w ',num2str(w),' deg']);
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' SetValue MainSequence.SegmentList.Initial_State.InitialState.Keplerian.RAAN ',num2str(RAAN),' deg']);
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' SetValue MainSequence.SegmentList.Initial_State.InitialState.Keplerian.TA ',num2str(TA),' deg']);
%% 二体传播
Propagate=satellite.Propagator.MainSequence.Item(1);
Propagate.PropagatorName='Earth Point Mass';
root.ExecuteCommand(['Astrogator */Satellite/',SatName,' RunMCS']);% 插入目标星
SatName2 = 'Chaser';       %  SAR_   GX_   Sat_  GX_1_  SAR_1_
satellite2 = root.CurrentScenario.Children.New('eSatellite', SatName2);
satellite2.SetPropagatorType('ePropagatorAstrogator');   %  不设置的时候默认为二体模型  ePropagatorJ4Perturbation
satellite2.Propagator;
InitialState2=satellite2.Propagator.MainSequence.Item(0);
InitialState2.CoordSystemName='Satellite/Target VVLH';
Z=0.1;
n=sqrt(3.986e5/sma^3);
Vx1 =  n*(2+Ecc);
Vx2 = (1+Ecc)^(1/2)*(1-Ecc)^(3/2);
Vx  = Vx1/Vx2 * Z;InitialState2.Element.X=0;
InitialState2.Element.Y=0;
InitialState2.Element.Z=Z;
InitialState2.Element.Vx=Vx;
InitialState2.Element.Vy=0;
InitialState2.Element.Vz=0;
Propagate2=satellite2.Propagator.MainSequence.Item(1);
Propagate2.PropagatorName='Earth Point Mass';
root.ExecuteCommand(['Astrogator */Satellite/',SatName2,' RunMCS']);% 报告二颗卫星的三维关系
satellite.VO.OrbitSystems.InertialByWindow.IsVisible=0;
satellite2.VO.OrbitSystems.InertialByWindow.IsVisible=0;
satellite2.VO.OrbitSystems.Add('Satellite/Target VVLH System')
satellite.VO.Vector.RefCrdns.Item(2).Visible=1;targetdata=root.ExecuteCommand(['Report_RM */Satellite/Target  Style "VVLH" TimePeriod "26 Jan 2024 04:00:00.000" "26 Jan 2024 16:00:00.000" TimeStep 60']);
Num=targetdata.Count;
for j=1:Num-2struct=regexp(targetdata.Item(j),',','split');Tar_x(j)=str2double(struct{2});Tar_y(j)=str2double(struct{3});Tar_z(j)=str2double(struct{4});
end
%
figure(1)
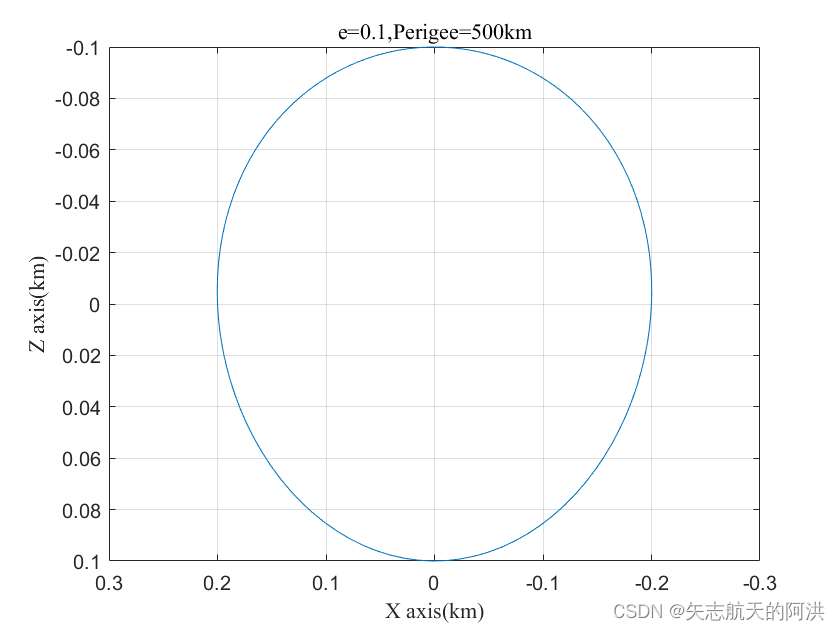
plot(Tar_x(1:220),Tar_z(1:220));set(gca,'XDir','reverse');
set(gca,'YDir','reverse');
xlabel('X axis(km)','FontName','Times New Roman')
ylabel('Z axis(km)','FontName','Times New Roman')
title('e=0.1,Perigee=500km','FontName','Times New Roman')figure(2)
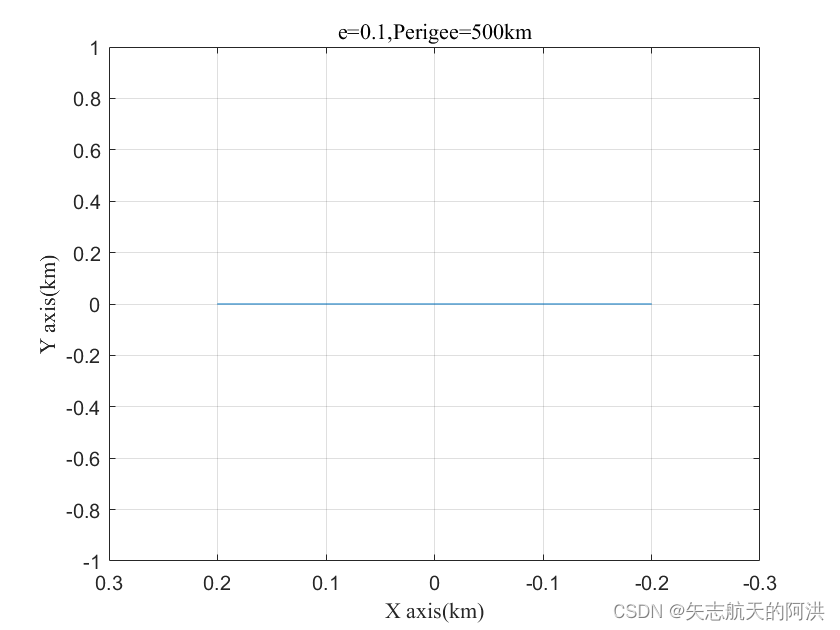
plot(Tar_x(1:220),Tar_y(1:220));set(gca,'XDir','reverse');
xlabel('X axis(km)','FontName','Times New Roman')
ylabel('Y axis(km)','FontName','Times New Roman')
title('e=0.1,Perigee=500km','FontName','Times New Roman')
grid on