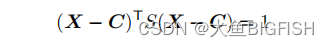椭圆专题
OpenCV结构分析与形状描述符(11)椭圆拟合函数fitEllipse()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C++11 算法描述 围绕一组2D点拟合一个椭圆。 该函数计算出一个椭圆,该椭圆在最小二乘意义上最好地拟合一组2D点。它返回一个内切椭圆的旋转矩形。使用了由[90]描述的第一个算法。开发者应该注意,由于数据点靠近包含的 Mat 元素的边界,返回的椭圆/旋转矩形数据
(4)SVG-path中的椭圆弧A(绝对)或a(相对)
1、概念 表示经过起始点(即上一条命令的结束点),到结束点之间画一段椭圆弧 2、7个参数 rx,ry,x-axis-rotation,large-arc-flag,sweep-flag,x,y (1)和(2)rx,ry rx:椭圆的x轴半径(即水平半径) ry:椭圆的y轴半径(即垂直半径) 这两个参数好理解,就是椭圆的两条对称轴半径,相等即为圆 也可以写比例,写比例时默认用符合条件
python实现椭圆曲线加密算法(ECC)
目录 椭圆曲线加密算法(ECC)简介ECC的数学基础椭圆曲线的定义ECC的基本操作 ECC加密和解密流程Python面向对象实现ECC加密和解密代码解释场景应用:安全通信总结 椭圆曲线加密算法(ECC)简介 椭圆曲线加密算法(Elliptic Curve Cryptography, ECC)是一种基于椭圆曲线数学结构的公钥加密算法。ECC以其较高的安全性和较小的密钥长度而闻名
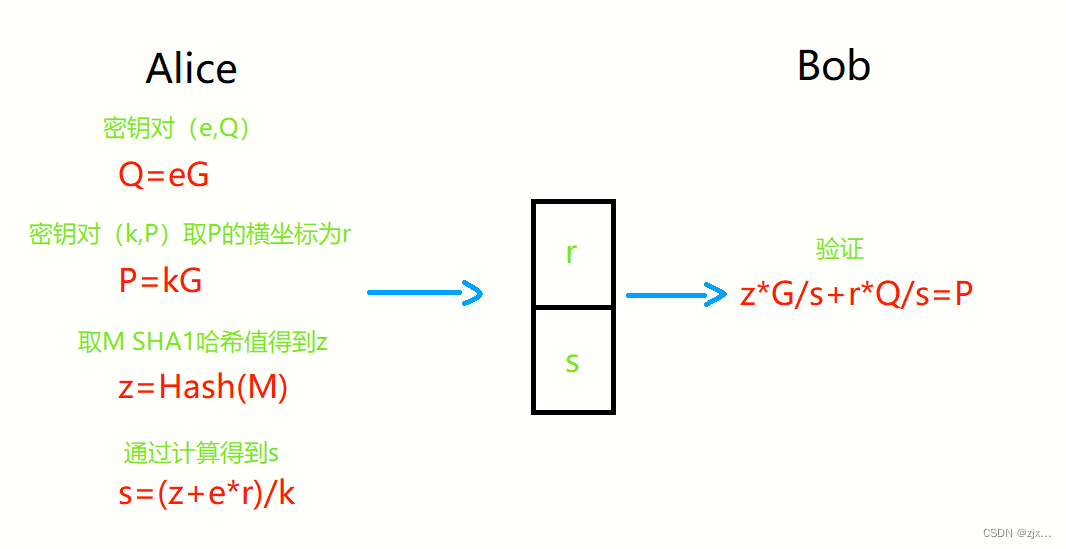
零知识证明-椭圆曲线(四)
前言 零知识证明(Zero—Knowledge Proof),是指一种密码学工具,允许互不信任的通信双方之间证明某个命题的有效性,同时不泄露任何额外信息 上章介绍了基础数字知识,这章主要讲 椭圆曲线 方程 2:椭圆曲线方程 y2+axy+by=x3+cx2+dx+e 式中,a、b、c、d、e均为实数,x和y在实数集上取值。 在加密领域一般采用如下简化后的数学形式: 有限域椭圆曲线 y2= x3+
OpenCV绘图函数(7)从一个椭圆定义中提取出多边形的顶点坐标函数ellipse2Poly()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C++11 算法描述 近似一个椭圆弧为一个多边形线。 函数 ellipse2Poly 计算近似指定椭圆弧的多边形线的顶点。它被 ellipse 函数所使用。如果 arcStart 大于 arcEnd,它们会被交换。 函数原型1 void cv::ellipse2
前端使用 Konva 实现可视化设计器(21)- 绘制图形(椭圆)
本章开始补充一些基础的图形绘制,比如绘制:直线、曲线、圆/椭形、矩形。这一章主要分享一下本示例是如何开始绘制一个图形的,并以绘制圆/椭形为实现目标。 请大家动动小手,给我一个免费的 Star 吧~ 大家如果发现了 Bug,欢迎来提 Issue 哟~ github源码 gitee源码 示例地址 接下来主要说说: UIGraph(图形)canvas2svg 打补丁拐点旋转修复 UI -
关于椭圆的方程(有Python画的动图)
关于椭圆的方程(有Python画的动图) flyfish 几何定义 椭圆是平面上所有到两个固定点(焦点)的距离之和为常数的点的集合。这两个固定点叫做焦点。 解析几何描述 设椭圆的两个焦点为 F 1 F_1 F1 和 F 2 F_2 F2,焦距(两焦点之间的距离的一半)为 c c c,长轴的半长轴为 a a a,短轴的半短轴为 b b b,椭圆上任意一点到这两个焦点的距离之
椭圆的标准方程与协方差矩阵的特征值和特征向量的关系
椭圆的标准方程与协方差矩阵的特征值和特征向量的关系 flyfish 单位圆 :单位圆表示在标准正交基下的分布。 椭圆 :通过协方差矩阵的特征向量和特征值变换得到的椭圆,表示数据在新的坐标系下的分布。 特征向量 :红色箭头表示特征向量方向,即椭圆的主要轴方向。 特征值 :红色箭头的长度表示特征值大小,即椭圆沿主要轴的伸缩程度。 import numpy as npimport ma
高级数字签名之椭圆曲线数字签名算法(ECDSA)
@TOC 1. 算法简述 该算法是微软操作系统及办公软件的序列号验证算法。 ECDSA(Elliptic Curve Digital Signature Algorithm, 椭圆曲线数字签名算法) 于1999年作为ANSI标准, 并于2000年成为IEEE和NIST标准。 ECDSA算法具有速度快、强度高、签名短等有点。 3. 代码实现 Java中未对该算法做实现, 而在Bouncy
IOS Quartz 各种绘制图形用法---实现画图片、写文字、画线、椭圆、矩形、棱形等
- (void)drawRect:(CGRect)rect { CGContextRef context = UIGraphicsGetCurrentContext(); /*NO.1画一条线 CGContextSetRGBStrokeColor(context, 0.5, 0.5, 0.5, 0.5
PCL 拟合二维椭圆(迭代法)
文章目录 一、简介二、实现代码三、实现效果参考资料 一、简介 一般情况,我们会用椭圆拟合二维点,用椭球拟合三维点。在n维中,这些对象被称为超椭球体,由二次方程隐式定义 超椭球的中心是n×1向量C,n×n矩阵S是正定的,n×1向量X是超椭球上的任意点。矩阵S可以用特征分解,S = R D R T RDR^T RD
椭圆曲线加密算法中公钥与私钥互换性分析
PrimiHub一款由密码学专家团队打造的开源隐私计算平台,专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。 在现代密码学中,椭圆曲线加密算法(Elliptic Curve Cryptography, ECC)因其高效的加密速度、较小的密钥尺寸和较高的安全性而受到广泛关注。ECC基于椭圆曲线数学,利用椭圆曲线上的点构成的阿贝尔群和相应的离散对数问题来实现加密和数字
PCL 绘制二维椭圆
文章目录 一、简介二、实现代码三、实现效果 一、简介 与绘制圆形相同,我们将椭圆使用参数t进行表示(参数化): 其中, t ∈ [ 0 , 2 ∗ π ] t\in[0,2*\pi] t∈
Android计算点击坐标是否在圆内和椭圆内
最近工作需要,顺带学了波数学。 要判断点是否在圆内,可以使用圆的几何性质:如果点的坐标(x, y)满足(x - 圆心x)^2 + (y - 圆心y)^2 < 半径^2,则该点在圆内。 计算点击坐标是否在圆内 // 圆的半径float radius =circleView.getWidth() / 2;// 按下的坐标float touchX = event.getX();float
opencv 皮肤检测 椭圆模型+轮廓去噪
一、经过前人学者大量的皮肤统计信息可以知道,如果将皮肤信息映射到YCrCb空间,则在CrCb二维空间中这些皮肤像素点近似成一个椭圆分布。 如果我们得到了一个皮肤CrCb的椭圆,我们只需判断它是否在椭圆内(包括边界),如果是,则可以判断其为皮肤,否则就是非皮肤像素点。 void ellipse(Mat& img, Point center, Size axes, double angle,
如何用MFC画出直线、虚线、折线、圆、椭圆、矩形、弧形(附上源码)
我创建的工程名字是默认的,叫MFCApplication3 首先在MFCApplication3Dlg.h这个文件中添加构造说明: public:CPen m_pen[5];CPoint m_point[5];public:void DrawLine(CDC *pDC);void DrawPolyline(CDC *pDC);void DrawPolygon(CDC *pDC);void
椭圆轨道的周期性运动轨道
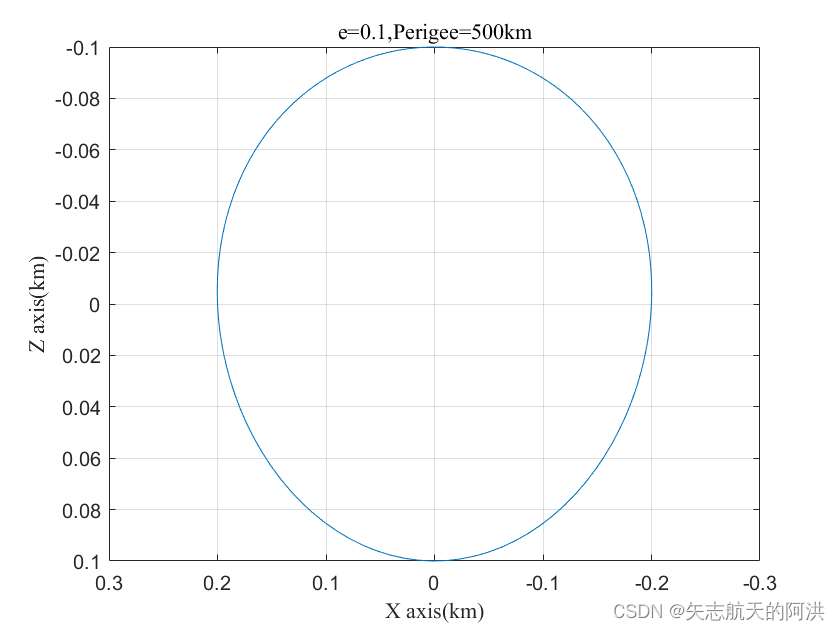
一、背景介绍 本节将从轨道六根数的角度,探究目标星为椭圆轨道,追踪星周期性环绕目标的必要条件。根据航天动力学的原理,对于一个椭圆轨道,其轨道能量为 对于能够不产生漂移的情况,绕飞编队的能量。对于追踪星到目标星的能量差,可以写 因此,对于零能量差的形式可以写为 通过使用下列离心率的关系 式中:为轨道近地点位置,所以离心率偏差可以写为近地点角的偏差,即 通过对上式修改,
Quartz 2d 用CGContextRef 绘制各种图形 (文字、圆、直线、弧线、矩形、扇形、椭圆、三角形、圆角形、贝塞尔曲线、图片)
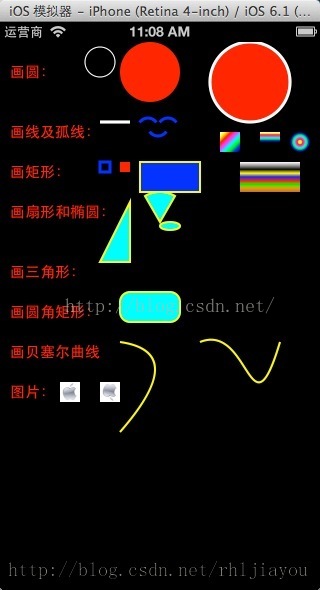
首先了解下 CGContextRef Graphics Context是图形上下文,可以将其理解为一块画布,我们可以在上面进行绘画操作,绘制完成后,将画布放到我们的View 中显示即可,View看着是一个画框。 自己学习时实现的Demo,希望对大家有帮助,具体的实现看代码,并有完美的注释解释,还有一些对我们帮助的博文供大家参考。 看下Demo 效果图先: 自定义Cu
OpenCV如何为等值线创建边界旋转框和椭圆(63)
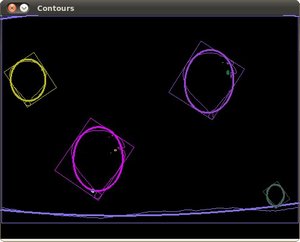
返回:OpenCV系列文章目录(持续更新中......) 上一篇:OpenCV 为轮廓创建边界框和圆(62) 下一篇:OpenCV的图像矩(64) 目标 在本教程中,您将学习如何: 使用 OpenCV 函数 cv::minAreaRect使用 OpenCV 函数 cv::fitEllipse cv::minAreaRect 和 cv::fitEllipse 都是 OpenCV
OpenCV08绘制线、矩形、圆、椭圆等基本几何形状,添加文字
/* txwtech2021.3.28OpenCV08 绘制形状与文字 使用cv::Point与cv::Scalar 绘制线、矩形、圆、椭圆等基本几何形状 随机生成与绘制文本 Point表示2D平面上一个点x,y Point p; p.x = 10; p.y = 8; or p = Pont(10,8); Scalar表示四个元素的向量 Scalar(a, b, c);// a = blue,
【区块链】椭圆曲线数字签名算法(ECDSA)
本文主要参考: 一文读懂ECDSA算法如何保护数据 椭圆曲线数字签名算法 1. ECDSA算法简介 ECDSA 是 Elliptic Curve Digital Signature Algorithm 的简称,主要用于对数据(比如一个文件)创建数字签名,以便于你在不破坏它的安全性的前提下对它的真实性进行验证。 你不应该将 ECDSA 与用来对数据进行加密的 AES(高级加密标准)相混
Trias技术丨关于椭圆曲线密码学的探究
椭圆曲线密码学(ECC),是一种基于椭圆曲线数学诞生的非对称秘钥加密的算法,加密过后只有特定的人才能对其进行解密。例如,ECC可用于确保用户在发送电子邮件时,除了收件人之外,没有人可以阅读这封邮件。 椭圆曲线是近几十年来被广泛探索的一个重要数学新领域。它作为一种解决复杂数字问题的工具,以及在密码学中的应用显示出巨大的潜力。 本文内容整理自Trias技术团队与北大软微学院的学术沙龙活
密码学 | 椭圆曲线密码学 ECC 入门(二)
目录 4 椭圆曲线:更好的陷门函数 5 奇异的对称性 6 让我们变得奇特 ⚠️ 原文地址:A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography ⚠️ 写在前面:本文属搬运博客,自己留着学习。如果你和我一样是小白,那么看完本文我们将仍然不能理解下图具体是在干什么,但能够对 RSA 和
密码学 | 椭圆曲线密码学 ECC 入门(一)
目录 正文 1 公共密钥密码学的兴起 2 玩具版 RSA 算法 2.1 RSA 基本原理 2.2 RSA 举例说明 1 加密 2 解密 3 不是完美的陷门函数 ⚠️ 原文地址:A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography ⚠️ 写在前面:本文属搬运博客,自