本文主要是介绍音频信号周期性的判断及周期测量,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
对于一般的周期信号 ,将 展开成傅里叶级数得:
f ( t ) = ∑ n = − ∞ ∞ F n e j n w 1 t f(t)=\sum\limits_{n=-\infty }^{\infty }{{{F}_{n}}{{e}^{jn{{w}_{1}}t}}} f(t)=n=−∞∑∞Fnejnw1t
将上式两边取傅里叶变换得:
F [ f ( t ) ] = 2 π ∑ n = − ∞ ∞ F n δ ( ω − n ω 1 ) F[f(t)]=2\pi \sum\limits_{n=-\infty }^{\infty }{{{F}_{n}}\delta (\omega -n{{\omega }_{1}})} F[f(t)]=2πn=−∞∑∞Fnδ(ω−nω1)
对于傅里叶级数,在时域中是一个周期且连续的函数,而在频域是一个非周期离散的函数,由一系列的冲激函数组成的离散频谱,且冲击发生在信号的谐波频率处。对于傅里叶变换,在时域中是一个非周期的连续函数,在频域是一个非周期的连续函数,所以在频谱上不可能有大的阶跃。
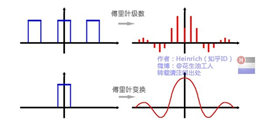
根据时域中周期信号和非周期信号在频域中特性的不同,可通过设定功率门限值,如果有大于门限值的频谱存在就是时域的周期信号,反之则不是。当判信号为周期信号时,将信号送入比较器,产生的脉冲信号送入单片机计数从而判断其周期。经过多次试验,选择一个较好的门限值,这样就能判断很大部分的信号(如三角波、锯齿波、正弦波)是否具有周期性,从而准确计算出信号的周期。
这篇关于音频信号周期性的判断及周期测量的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







