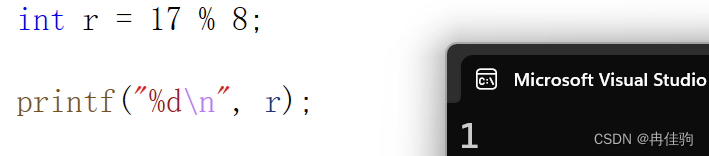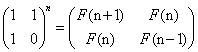取模专题
排列数+时间戳+逆元取模
前言:这个题目是真的难,不会做,看了题解才发现是咋回事 题目地址 最主要的就是为啥是除以3,c之前需要完成a 和 b,d 和 e 对我们的答案没有影响,所以我们要除以 A(3,3) ,但是 a 和 b 的排列没有要求,所以乘以 A( 2 , 2 ) 抵消得到 3 #include<bits/stdc++.h>using i64 = long long;using u64 =
CSU - 1556 Jerry's trouble(快速幂取模)
【题目链接】:click here 【题目大意】:计算x1^m+x2^m+..xn^m(1<=x1<=n)( 1 <= n < 1 000 000, 1 <= m < 1000) 【解题思路】:快速幂取模 代码: solution one: #include<bits/stdc++.h>#define LL long longusing namespace std;const
UESTC 1712 Easy Problem With Numbers 除法对和数取模,分解,线段树
附上神牛原版思路: 如果这个题只有乘法,那么你肯定会做吧?线段树更新区间查找区间。 那么有除法呢?当一个数x和m互质的时候,除以x可以改为乘以x的逆元。(至于互质的数求逆元用扩展欧几里德,这个网上可以随便找到) 但是这题并不能保证除的数与m互质吧?什么时候x与m不互质呢?就是x与m含有公因子吧? 那么我们一开始就把m分解,分解出来m有p1,p2,p3,p4...pn等一
mycat水平分库-对用户id取模
schema.xml: <?xml version="1.0"?><!DOCTYPE mycat:schema SYSTEM "schema.dtd"><mycat:schema xmlns:mycat="http://io.mycat/"><schema name="TESTDB" checkSQLschema="false" sqlMaxLimit="100" ><table name=
JavaScript 取模应用 各行换色
<!DOCTYPE HTML> <html> <head> <meta charset="utf-8"> <title>无标题文档</title> <script> window.οnlοad=function () { var aLi=document.getElementsByTagName('li'); for(var i=0;i<aLi.le
算数操作符(除法操作符和取模操作符)
目录 / --- 除法操作符 整数除法 代码举例说明 代码验证 浮点数除法 代码举例说明 代码验证 % --- 取模操作符 代码举例说明 代码验证 除法操作符和取模操作符的相关案例 / --- 除法操作符 整数除法 除号的两端都是整数,执行的就是整数除法整数除法的运行规则:只保留商,去掉余数 代码举例说明 int r = 7 / 2;pri
hdu4506(快速幂取模)
小明系列故事——师兄帮帮忙 Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others) Total Submission(s): 4112 Accepted Submission(s): 1069 Problem Description 小明自从告别了ACM/IC
poj 3358 Period of an Infinite Binary Expansion(数论:欧拉函数+快速幂取模)
不太好理解题意的一道题 给出一个除式 要求找到对应二进制的循环起点和最小循环节长度 这里还考察了分数化小数的知识点。。。 这点不会难怪看题解都觉得很吃力 1/10 分数化小数的规律如下: 0.1 0.2 0.4 0.8 1.6 1.2 0.4(每次取左侧一位×2,如果大于10,小数位取1,再把这一位%10) 0 0 0 0 1 1 0 以1/1
poj 3070 Fibonacci(矩阵快速幂取模)
之前就听过这个东西 但是一直没遇到这个类型的题目 这道题就是典型的矩阵快速幂模板题了 根据斐波那契数列的性质以及矩阵快速幂的做法 可知: 0ms代码如下: #include <cstdio>#include <cstring>#define M 10000using namespace std;struct Matrix {int matrix[2][2];Matrix
取模软件测试版生成的有斜线,但测试字库的功能是好用无限制。只需要自己开发一个字库生成软件。IDA工具,如何搜中文
IDA工具,如何搜中文 在 IDA (Interactive Disassembler) 中搜索中文字符串,可以按照以下步骤操作: 方法一:使用“搜索文本”功能 打开 IDA 并加载目标文件:启动 IDA 并打开你需要分析的二进制文件。打开搜索文本对话框: 在 IDA 的菜单栏中,选择 Search > Text...,或者按快捷键 Alt+T。 输入中文字符串: 在弹出的搜索对话框中,
hdu4704--sum--大数幂取模
做这道题学到了好多好多知识,想起了一些被遗忘的知识,收获还是很大的。 1.费马小定理的应用。首先说明一下什么是费马小定理:假如P是质数,且gcd(a,p)=1(即a,p互质),则a^(p-1)===1(mod p)。 应用为:若P为质数,且gcd(a,p)=1,则可以计算 a^n mod p的值。(n为一个无法用long long存下的大数(若不为大数直接用快速幂其实就可以了))
FZU 2018 计数 快速幂取模
题意:对于方程 x^x = a(mod p), PH想知道对于[0,p-1]内的数,有多少个这样的x满足这个方程。请注意,虽然对于0^0的值有争论,甚至不一定有意义,可是在本题中,PH认为0^0 = 1。 #include <iostream>#include <cstdio>#include <cstring>using namespace std;const int MAXN = 1
求a的b次方、a的b次方对m取模
求a的b次方、a的b次方对m取模 快速计算乘方的算法,求a的b次方 如计算2^13,则传统做法需要进行12次乘法,但是可以优化: 把2*2的结果保存起来看看,是不是成了:4*4*4*4*4*4*2 再把4*4的结果保存起来:16*16*16*2 一共5次运算,分别是2*2、4*4和16*16*16*2 这样分析,我们算法因该是只需要计算一半都不到的乘法了。
快速幂/快速幂取模/矩阵求解快速幂
因为做了一个Fibonacci的题需要用矩阵+快速幂求解所以引发了下面一系列问题!!! 快速幂: 快速幂时间复杂度为 O(log2N), 与朴素的O(N)相比效率有了极大的提高。 例如: 3 ^ 999 = 3 * 3 * 3 * … * 3 直接乘要做998次乘法。但事实上可以这样做: 3 ^ 2 = 3 * 3
nyoj-205--求余数--(大整数取模)
题目链接:http://acm.nyist.net/JudgeOnline/problem.php?pid=205 #include<stdio.h>#include<string.h>int main(){int n,l,i,sum;char s[1000000];scanf("%d",&n);getchar();while(n--){gets(s);l=strlen(s);sum=
快速幂取模运算(Modular Exponentiation)
不考虑取模的快速幂运算(迭代法) /* Iterative Function to calculate (x^y) in O(logy) */int power(int x, unsigned int y){int res = 1; // Initialize resultwhile (y > 0){// If y is odd, multiply x with resultif (
Js 取模运算、取商、取整方法
//求余数 document.write(1%4); document.write(6%4); //求商 console.info(1/4); console.info(6/4); //求商,取整 console.info(parseInt(1/4)); console.info(parseInt(6/4)); console.info('----'); /
牛客网:S老师的公式 ← 取模运算
【题目来源】https://ac.nowcoder.com/acm/contest/76652/A【题目描述】 S 老师丢给你了一个简单的数学问题: 求 。 请你求出答案。【输入格式】 一行一个整数 n (1≤n≤10^6)。【输出格式】 一行一个整数表示答案。【说明】 例如,若n=3,则本题求解 gcd(1+2+3,1*2*3)=gcd(6,6)=6【算法分析】 ● 辗转相除法求最大公约数:ht
取模学习之Image2Lcd
使用软件Image2Lcd V0.4 1.:打开图片,图片格式可选如下图,本文使用的.jpg格式 转换后数组例子(数组头数据占前8字节): 2.:扫描模式 由第1个字节低四位配置 (1)水平扫描 0x00 (2)垂直扫描 0x01 (3)数据水平 字节垂直 0x02 (4)数据垂直 字节水平 0x03 3.:第1个字节高四位配置 (1)字节内像素数据反序 0x20