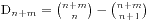卡特兰专题
hdu4828（卡特兰数+逆元）
这题的前几个数据分别为1,2,5,14,32......................然后确定这是个卡特兰数列 下面来介绍下卡特兰数,它的递推式为f[i+1] = f[i]*(4*n - 6)/n，其中f[2] = f[3] =1;f[4] = 2;f[5] = 14;f[6] = 32.................................. 但是这题的n太大了，所以要用到逆元，
HDU 1130(卡特兰数，大数)
题意：如题。 import java.util.*;import java.math.*;public class Main{public static void main(String[] args) {int n;Scanner in=new Scanner(System.in);BigInteger one=BigInteger.ONE;BigInteger four
hdu 2067 小兔的棋盘 （卡特兰数的应用）
/******************* Author:fisty* Data:2014-10-19* hdu 2067*****************/#include <cstdio>#include <algorithm>using namespace std;long long f[110];//卡特兰数int main(){f[0]=1;for(int i=1;i<=35;i
UVa 991 Safe Salutations 卡特兰数
题目来源：UVa 991 Safe Salutations 题意：圆上2*n个点均匀分布 两两相连 求不相交的方案数 思路：卡特兰数的应用 以下总结转自某大牛 /*最典型的四类应用：（实质上却都一样，无非是递归等式的应用，就看你能不能分解问题写出递归式了）1.括号化问题。矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化
uva 10303 - How Many Trees?(卡特兰数）
题目链接：uva 10303 - How Many Trees? 卡特兰数，公式num[i + 1] = num[i] * (4 * i - 6) / i ( i ≥ 3)。 #include <stdio.h>#include <string.h>#include <iostream>using namespace std;const int N = 6005;str
【CF1924D】Balanced Subsequences 【卡特兰数，组合数，数学】
C F 1924 D . CF1924D. CF1924D.Balanced Subsequences 题意为：给定 n , m , k n,m,k n,m,k，求有多少个由 n n n 个 (， m m m 个 ) 组成的序列满足最长的合法括号子序列的长度恰为 2 k 2k 2k（对 1 0 9 + 7 10^9+7 109+7 取模）。 思路 我们很容易想到这跟 C a t
卡特兰数（Catalan）的原理和题目
Catalan数的定义令h(1)=1，Catalan数满足递归式：h(n) = h(1)*h(n-1) +h(2)*h(n-2) + ... + h(n-1)h(1)，n>=2该递推关系的解为： 证明： 令1表示进栈，0表示出栈，则可转化为求一个2n位、含n个1、n个0的二进制数，满足从左往右扫描到任意一位时，经过的0数不多于1数（也就是1的个数>=0的个数)。显然含n个1、n个0的2n位二进
算法 卡特兰Catalan数
介绍 Catalan数是组合数学中一个常在各种计数问题中出现的数列。一般项公式为 Cn的另一个表达形式为 一般来说，我们编程时使用递推关系会更方便计算 或 即：C(n) = C(1)*C(n-1) + C(2)*C(n-2) + … + C(n-1)C(1). 它的前几项为: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796。可以先通
hdu 1131 卡特兰数，大数
这道题和hdu1130 是姊妹题。 hdu 1130是典型的卡特兰数题。这题又加了标签，所以总数是卡特兰数乘以n的阶乘。 /** create by zzy at 2017,2:03:40 PM*/import java.math.BigInteger;import java.util.Scanner;public class Main {static int max=105;sta
leetcode - 96. Unique Binary Search Trees【卡特兰数 + 整数处理注意】
题目 Given n, how many structurally unique BST's (binary search trees) that store values 1...n? For example, Given n = 3, there are a total of 5 unique BST's. 1 3 3 2 1\
UVa 10303 How Many Trees? (卡特兰数高精度)
10303 - How Many Trees? Time limit: 3.000 seconds http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=115&page=show_problem&problem=1244 A binary search tree is a bina
![[递归与递推] 栈与卡特兰数](https://img-blog.csdnimg.cn/img_convert/59d08e3624e3d4aa59626c792c656c84.png)
[递归与递推] 栈与卡特兰数
题目背景 栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。 栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。 栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。 题目描述 宁宁考虑的是这样一个问题：一个操作数
快速求第n个卡特兰数模板
卡特兰数的应用：https://blog.csdn.net/SunPeishuai/article/details/81407126 快速求第n位卡特兰数 模板： 递推法： /*通过递推 求卡特兰数的方法*/#include<cstdio>#include<iostream>using namespace std;int main(){int n=0;scanf("%d", &n)
卡特兰数的应用，你知道几个？
来自：https://blog.csdn.net/zhangmh93425/article/details/44677891 卡特兰递推公式 1. 2. 3. 4. 5. 卡特兰数的应用 1. 由n个+1和n个-1构成2n项其部分和满足的序列个数等于第n个Catalan数。 假设不满足条件的序列个数为，那么就有。而对于不满足的序列，必然存在某一个奇数位使，而且
C++ 数论相关题目：卡特兰数应用、快速幂求组合数。满足条件的01序列
给定 n 个 0 和 n 个 1 ，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。 输出的答案对 109+7 取模。 输入格式 共一行，包含整数 n 。 输出格式 共一行，包含一个整数，表示答案。 数据范围 1≤n≤105 输入样例： 3 输出样例： 5 上述描述了本题的公式
csu 1950: 谈笑风生 卡特兰数
题目链接点这里 基佬出的毒瘤题啊。。。 看完题目我们很容易把第x个左括号和其右括号内的看成独立一部分设为Q，枚举这个里面的括号数。这里很简单，， 然后那？，，然后还剩下Q左右的2部分。。接下来该怎么考虑？。。一开始我是把2部分放在一起考虑的，结果非常复杂，考虑的东西非常多 其实那，我们只需要单独考虑2部份就可以了。 我们需要知道一个公式：Cm(i,j)=C(i+j,j)
【leetcode系列】【算法】【中等】不同的二叉搜索树 II(卡特兰数问题))
题目： 题目链接： https://leetcode-cn.com/problems/unique-binary-search-trees-ii/ 解题思路： 如果只是求个数，可直接通过卡特兰数递推公式求解： 假设是卡特兰数的第n + 1项，则： 其中， 其他常见的符合卡特兰数递推公式的例子有：括号化、出栈次序、凸多边形三角划分、n对括号正确匹配数目 所以如果不需要列
卡特兰数 hdu 5673
卡特兰数的性质 卡特兰数有一些优美的性质，如 通项公式一 Cn=1n+1Cn2n=Cn2n−Cn−12n Cn=1n+1C2nn=C2nn−C2nn−1； 通项公式二 Cn=1n+1∑i=0n(Cin)2 Cn=1n+1∑i=0n(Cni)2； 递推公式一 Cn+1=2(2n+1)n+2Cn Cn+1=2(2n+1)n+2Cn，且 C0=1 C0=1；
HDU/HDOJ 2067 小兔的棋盘 DP/卡特兰数
HDU/HDOJ 2067 小兔的棋盘 小兔的棋盘 Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 12782 Accepted Submission(s): 6392 Problem Description 小兔
POJ 2084 卡特兰数
卡特兰数 百科名片 卡特兰数又称卡塔兰数，是组合数学中一个常出现在各种计数问题中出现的数列。由以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。 原理 令h(1)=1,h(2)=1，catalan数满足递归式： h(n)= h(1)*h(n-1)+h(2)*h(n-2) + ... + h(n-1)h(1) (其中n>=3)
Problem A:小兔的棋盘（卡特兰数）
题目链接 卡特兰数 求 (0,0到(n,n)的路径数 Problem Description 小兔的叔叔从外面旅游回来给她带来了一个礼物，小兔高兴地跑回自己的房间，拆开一看是一个棋盘，小兔有所失望。不过没过几天发现了棋盘的好玩之处。从起点(0，0)走到终点(n,n)的最短路径数是C(2n,n),现在小兔又想如果不穿越对角线(但可接触对角线上的格点)，这样的路径数有多少?小兔想了很长时间都没
用卡特兰数来求出栈序列个数
卡特兰数（Catalan数） 定义： 令h(0)=1，h(1)=1，Catalan数满足递归式：h(n) = h(0)*h(n-1) + h(1)*h(n-2) + … + h(n-1)*h(0) (n>=2) 该递推关系的解为：h(n) = C(2n,n)/(n+1)，n=0,1,2,3,… （其中C(2n,n)表示2n个物品中取n个的组合数） 原理： 令h(0)=1,h(1)=1，cata