[递归与递推] 栈与卡特兰数

本文主要是介绍[递归与递推] 栈与卡特兰数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

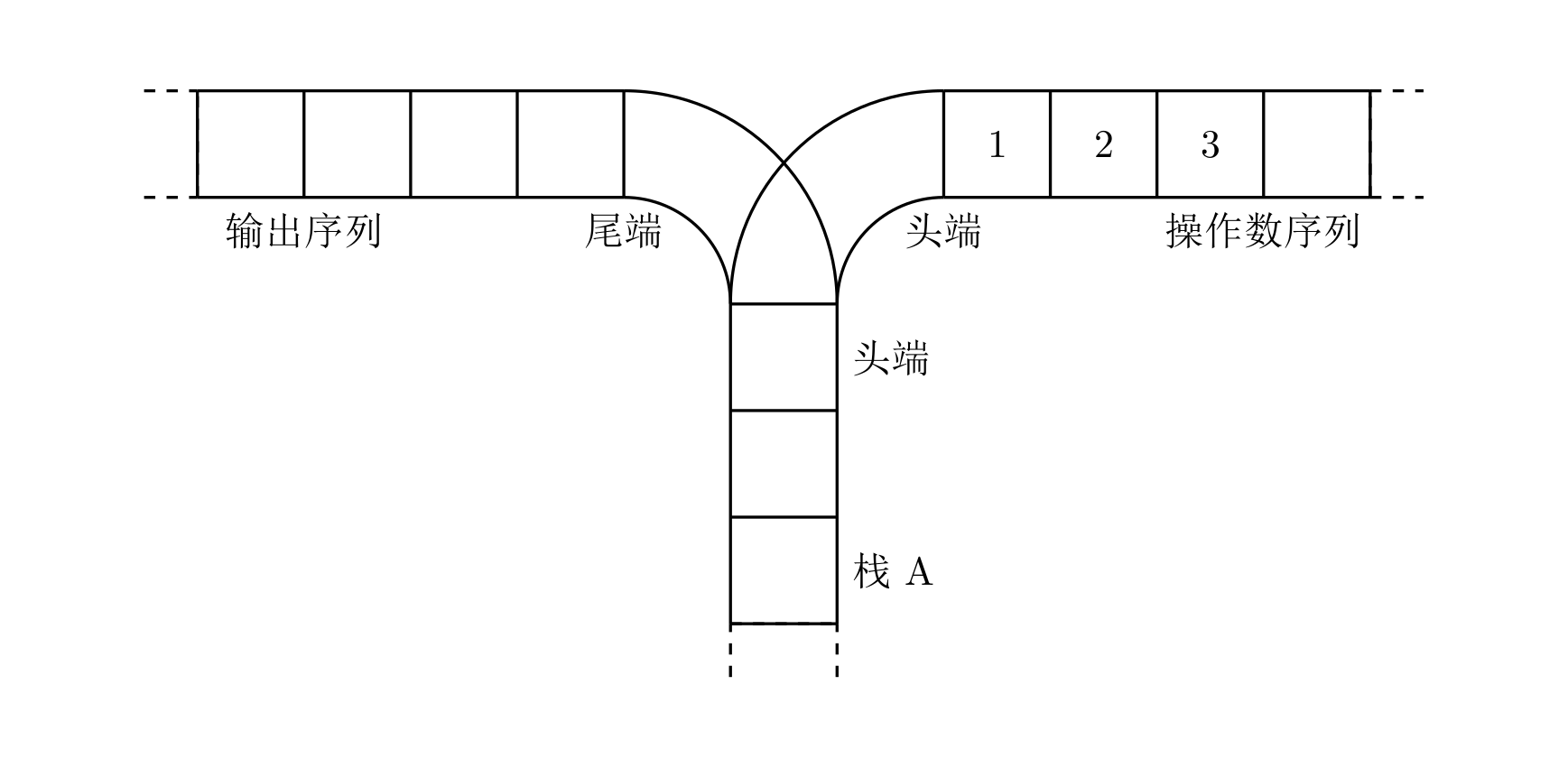
宁宁考虑的是这样一个问题：一个操作数序列，1,2,…,n（图示为 1 到 3 的情况），栈 A 的深度大于 n。

现在可以进行两种操作，

1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

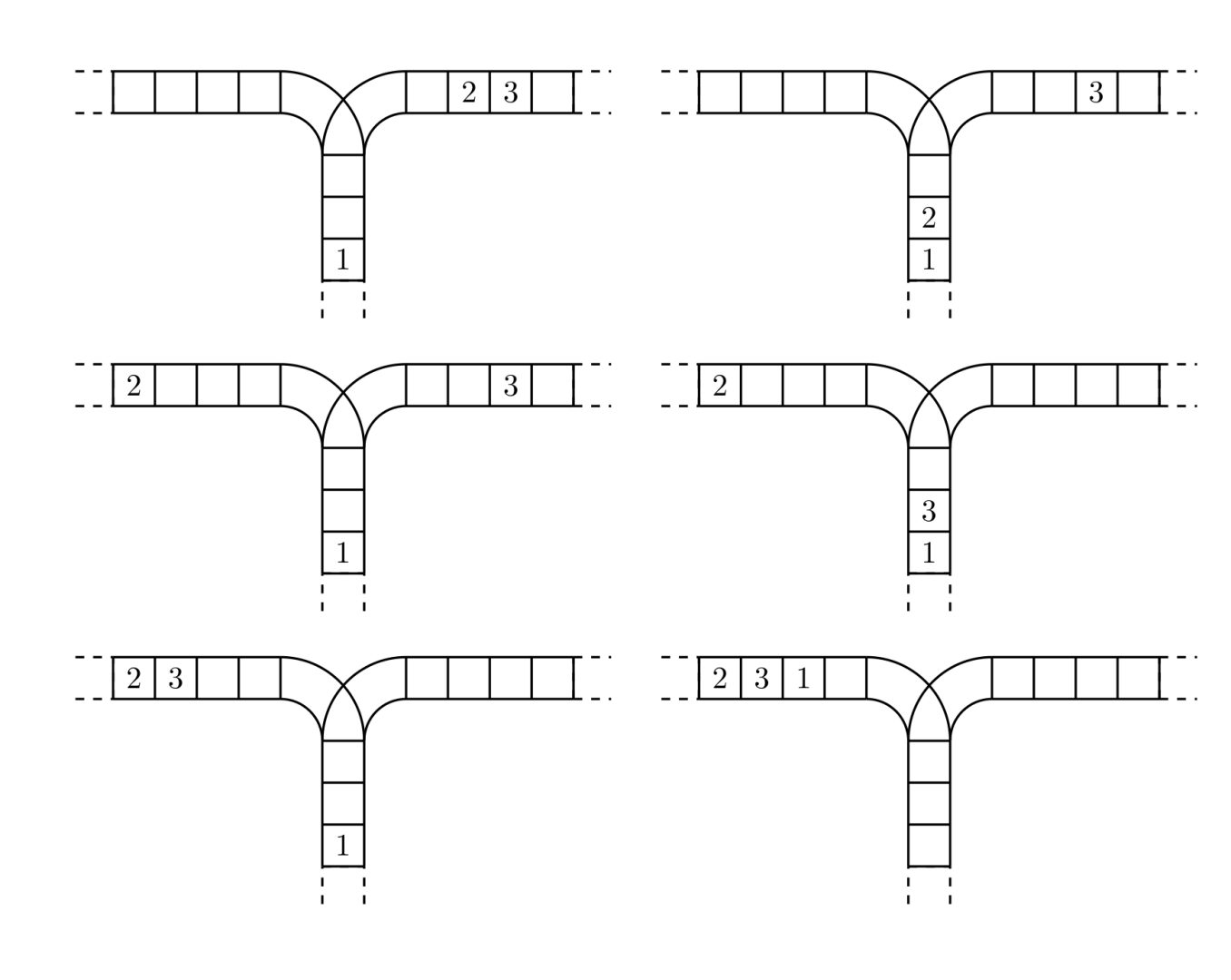
（原始状态如上图所示）

你的程序将对给定的 nn，计算并输出由操作数序列 1,2,…,n 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 n（1≤n≤18）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

输入输出样例

输入 #1

3

输出 #1

5

解题分析

先考虑一下本题的数量级，n<=18，我们知道，一个元素可以往往可以有三种操作，进栈，出栈，或者不出栈，等下一个元素进来出栈后再出栈。那么，如果我们去枚举的话，将要面对的是2^18甚至更高的枚举次数，这显然会导致超时。加上题目并未要求我们把每一个序列都输出，所以虽然题目有栈的背景，但是我们并不需要去使用这个数据结构。

考虑动态规划或者递推的做法，我们先来介绍一下动态规划的做法。我们可以这样去考虑一个函数f(i,j)，i代表在栈内的元素个数，j代表还未进栈的元素个数。先来考虑一些边界的特殊情况，当i为0时，可以自然地想到，我们这个时候只有一种操作，让栈外第一个元素进栈，于是有f(i,j)=f(i+1,j-1)；当j为0时，也就是元素都在栈内了，那没什么好说的，只能让元素出栈了，而且后续都是不停地让元素出栈，这个时候只有一种做法，固f(i,j)=1;接下来就是一个比较复杂的情况了，当栈内和栈外都有元素的时候，i>0,j>0，又该如何去考虑呢？这个时候我们考虑栈内的元素，它是可以出栈的，所以有一种情况是f(i-1,j)，考虑栈外的元素，它是可以进栈的，所以又有一种情况是f(i+1,j-1)，这个时候f(i,j)=f(i-1,j)+f(i+1,j-1)，至此，我们已经讨论完全部情况了，配合记忆化搜索的方法，本题很容易就解决了。

代码实现1

#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int dp[20][20];
int f(int i,int j){if(dp[i][j]) return dp[i][j];if(i==0){return dp[i+1][j-1]=f(i+1,j-1);}if(j==0){return 1;}return dp[i][j]=f(i+1,j-1)+f(i-1,j);
}int main(){int n;cin>>n;cout<<f(0,n)<<endl;return 0;
}

接下来我们分析一下递推的方法，这就涉及到一个特殊的数，卡特兰数。

大致是这么个意思，我们假定dp[i]为i个数依次进栈，随机出栈所能得到的序列个数，那么，我们很容易得到dp[0]=dp[1]=1; 接下来，我们考虑n个数，n>1的情况。

假定数x是最后一个出栈的元素，这是可以实现的，每个元素x我们都可以让比它小的数进栈后全出光再让它进栈，然后把它赖在栈底不走，出光比它大的数。那么，我们很容易就可以知道，当我们进行分类讨论时，我们可以以某个元素最后出栈为我们讨论的标准，那么，一共有x=1,2,3....n,共n种情况，其中当取定x时候，有x-1个数比x小，n-x个数比x大，根据组合数乘法原理，我们可以得到在这种情况下的方法数是f[x-1]*f[n-x]。

也就是说f[n]=f[0]*f[n-1]+f[1]*f[n-2]......f[n-1]*f[0]。

代码实现

#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int f[20]={0};int main(){f[0]=f[1]=1;int n; cin>>n;for(int i=2;i<=n;i++)for(int j=0;j<=i-1;j++){f[i]+=f[j]*f[i-j-1];}cout<<f[n]<<endl;return 0;
}

这篇关于[递归与递推] 栈与卡特兰数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---