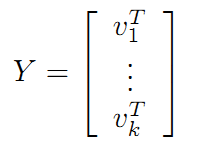svd专题

特征值分解(EVD)和奇异值分解(SVD)—应用于图片压缩

特征值分解(EVD)和奇异值分解(SVD)—应用于图片压缩目录前言一、特征值分解二、应用特征值分解对图片进行压缩三、矩阵的奇异值分解四、应用奇异值分解对图片进行压缩五、MATLAB仿真代码前言学习了特征值分解和奇异值分解相关知识，发现其可以用于图片压缩，但网上没有找到相应代码，本文在学习了之后编写出了图片压缩的代码，发现奇异值分

《机器学习》基于SVD的矩阵分解推导、案例实现

目录一、SVD奇异值分解 1、什么是SVD 2、SVD的应用 1）数据降维 2）推荐算法 3）自然语言处理 3、核心 1）什么是酉矩阵 2）什么是对角矩阵 4、分解过程二、推导 1、如何求解这三个矩阵 1）已知： 2）根据酉矩阵的特点即可得出：

SVD降维

文章目录一、SVD降维的基本原理二、SVD降维的步骤三、SVD降维的优点四、SVD降维的应用五、代码应用六、SVD降维的局限性一、SVD降维的基本原理 SVD是线性代数中的一种技术，它将一个矩阵A分解为三个矩阵的乘积：A = UΣV^T。其中，U和V是正交矩阵，Σ是对角矩阵，对角线上的元素称为奇异值。这些奇异值表示了矩阵A在各个方向上的“重要性”或“能量”。在降维过程中，

[干货汇总]LSA及SVD介绍

1. 前言近期在看关于NER(Named Entity Recognition)的paper，里面涉及到的几个机器学习的算法，需要学习一下，在网上看了一些相关干货，汇总一下前人智慧。首先贴出几篇写的还不错的blog blog1 LSA潜在语义分析该blog是在Wiki中翻译过来，翻译的反正比我看原文理解的好，进行初步了解还是不错的。 blog2 SVD矩阵奇异值分解 &&

基于Python的机器学习系列（23）：奇异值分解（SVD）

在本篇中，我们将介绍如何利用奇异值分解（SVD）进行降维。SVD 是一种强大的矩阵分解方法，可以帮助我们提取数据中的重要特征，广泛应用于数据分析、图像处理等领域。问题定义在数据分析中，特别是当数据维度很高时，我们经常需要减少数据的维度以便于处理和可视化。奇异值分解（SVD）提供了一种有效的方法来实现这一目标。SVD 通过将原始数据矩阵分解成三个矩阵的乘积，从

特征值分解（EVD)和奇异值分解(SVD）

两篇博文，写得很好： http://blog.sina.com.cn/s/blog_3f738ee00102val0.html http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html

PCA降维奇异值分解SVD

PCA降维涉及高维数据的问题容易陷入维数灾难，随着数据集维数的增加，算法学习所需的样本数量呈指数级增加，且需要更多的内存和处理能力，消耗资源。主成分分析也称为K-L变换，常用于高位数据预处理和可视化。PCA可以把可能具有相关性的高维变量合成线性无关的低维变量，称为主成分。原理就是PCA将高维具有相关性的数据进行线性变换映射到一个低维子空间，尽可能多的保留更多变量(代表原特征)，降维成一个线性无

各种数据降维方法ICA、 ISOMAP、 LDA、LE、 LLE、MDS、 PCA、 KPCA、SPCA、SVD、 JADE

独立分量分析 ICA 等度量映射 ISOMAP 线性判别分析 LDA (拉普拉斯)数据降维方法 LE 局部线性嵌入 LLE 多维尺度变换MDS 主成分分析 PCA 核主成分分析 KPCA 稀疏主成分分析SPCA 奇异值分解SVD 特征矩阵的联合近似对角化 JADE 各种数据降维方法(matlab代码)代码获取戳此处代码获取戳此处降维目的：克服维数灾难，获取本质特征，节省存储空

机器学习-SVD

机器学习中SVD总结 https://mp.weixin.qq.com/s/Dv51K8JETakIKe5dPBAPVg 目录：矩阵分解 1.1 矩阵分解作用 1.2 矩阵分解的方法 1.3 推荐学习的经典矩阵分解算法 SVD具体介绍 2.1 特征值、特征向量、特征值分解 2.2 SVD分解 2.3 SVD分解的应用 1. 矩阵分解 1.1 矩阵分解作用

机器学习-SVD分解

ref：https://www.cnblogs.com/lzllovesyl/p/5243370.html 本文先从几何意义上对奇异值分解SVD进行简单介绍，然后分析了特征值分解与奇异值分解的区别与联系，最后用python实现将SVD应用于推荐系统。 1.SVD详解 SVD(singular value decomposition)，翻译成中文就是奇异值分解。SVD的用处有很多，比如：LSA

机器学习实战 --- 利用SVD简化数据

SVD概述：奇异值分解（SVD， Singular Value Decomposition）: 提取信息的一种方法，可以把SVD看成是从噪声中抽取相关的特征。从生物信息学到金融学， SVD是是提取信息的巨大工具。 SVD场景：信息检索 - 隐形语义索引（Lstent Semantic Indexing, LSI）或隐形语义分析（LSA）。隐形语义索引

PCA使用SVD解决

http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html 主成分分析在上一节里面也讲了一些，这里主要谈谈如何用SVD去解PCA的问题。PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量，我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模

文本分类之降维技术之特征抽取之SVD矩阵的分解的原理的介绍

http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html 一、奇异值与特征值基础知识：特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法。两者有着很紧密的关系，我在接下来会谈到，特征值分解和奇异值分解的目的都是一样，就是提取出一个矩阵最重要的特征。先谈谈特征值分解吧：

【转】奇异值分解(SVD)原理详解及推导

本文转载于陈靖博客http://blog.csdn.net/zhongkejingwang/article/details/43053513 在网上看到有很多文章介绍SVD的，讲的也都不错，但是感觉还是有需要补充的，特别是关于矩阵和映射之间的对应关系。前段时间看了国外的一篇文章，叫A Singularly Valuable Decomposition The SVD of a Ma

【图像隐藏】基于奇异值分解SVD实现数字水印嵌入提取，相关系数NC附Matlab代码

以下是使用奇异值分解（SVD）实现数字水印嵌入和提取的相关系数（NC）的Matlab代码示例： matlab % 数字水印嵌入 function watermarked_image = embed_watermark(original_image, watermark, strength) % 将原始图像进行SVD分解 [U, S, V] = svd(double(original_image

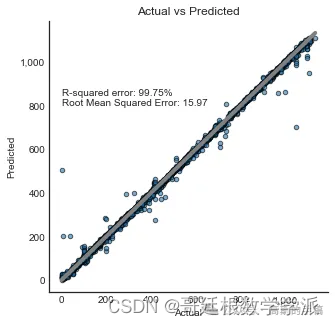
基于机器学习和奇异值分解SVD的电池剩余使用寿命预测（Python）

采用k-最近邻KNN和随机森林算法建立预测模型。 import pandas as pdfrom sklearn.model_selection import train_test_splitfrom sklearn.svm import SVC # Support Vector Classifierfrom sklearn.preprocessing import StandardSc

【机器学习】必会降维算法之：奇异值分解（SVD）

奇异值分解（SVD） 1、引言2、奇异值分解（SVD）2.1 定义2.2 应用场景2.3 核心原理2.4 算法公式2.5 代码示例 3、总结 1、引言一转眼，小屌丝：鱼哥，就要到每年最开心的节日了：六一儿童节。小鱼：你有啥想法？小屌丝：想法没有，玩的地方倒是想小鱼：拉倒吧，我可不去小屌丝：确定？小鱼：看情况。小屌丝：嘿嘿，难得过节日，我们也得放松一下小鱼：正

基于SVD的点云配准

前言为了更加深入透彻的理解点云配准，所以打算从头实现一次配准的过程，从关键点提取、特征提取、对应关系确定、SVD确定变换矩阵，一步一步完成。首先介绍一下配准过程中用到的一些函数 1. ISS3D关键点提取具体来说，它使用ISS（Intrinsic Shape Signatures）关键点检测算法在输入的点云数据中找到关键点

C语言 | 使用Jacobi方法实现SVD分解（附代码）

========================================== 博主github：https://github.com/MichaelBeechan 博主CSDN：https://blog.csdn.net/u011344545 ========================================== 原理

AIGC笔记--SVD中UNet加载预训练权重

1--加载方式 1. 加载全参数（.ckpt） 2. 加载LoRA（.safetensors） 2--简单实例 import syssys.path.append("/mnt/dolphinfs/hdd_pool/docker/user/hadoop-waimai-aigc/liujinfu/Codes/v3d-vgen-motion")import

基于音乐/电影/图书的协同过滤推荐算法代码实现（基于用户推荐、基于项目推荐、基于SlopeOne算法推荐、基于SVD算法推荐、混合加权推荐）

基于音乐/电影/图书的协同过滤推荐算法代码实现（基于用户推荐、基于项目推荐、基于SlopeOne算法推荐、基于SVD算法推荐、加权混合推荐）一、开发工具及使用技术 MyEclipse10、jdk1.7、tomcat7、jsp、javascript、jquery、bootstrap、webuploader、layer、ssh、mysql、navicat、mahout API等。二、开发过程

SVD求解Ax=0

源于计算机视觉life的LiDAR+视觉+IMU多传感器融合SLAM：原理推导+源码逐行详解+项目实战 SVD求解Ax=0 首先，我们需要了解四元数的基本概念。四元数是由三个虚部和一个实部组成的复数扩展，可以用来表示三维空间中的旋转。四元数的乘法规则如下： q 1 ⊗ q 2 = [ q 1 ] L q 2 = [ q 2 ] R q 1 q_1 \otimes q_2 = [q_1]_L

《机器学习实战》笔记之十四——利用SVD简化数据

第十四章利用SVD简化数据 14.1 SVD的应用特点：利用SVD能够用小得多的数据集来表示原始数据集。优点：简化数据，去除噪声，提高算法的结果。缺点：数据的转换可能难以理解。隐性语义索引（LSI）利用SVD的方法为隐性语义索引（Latent Semantic Indexing, LSI）或隐性语义分析（Latent Semantic Ana

关于SVD分解

转自http://leftnoteasy.cnblogs.com, 前言：上一次写了关于PCA与LDA的文章，PCA的实现一般有两种，一种是用特征值分解去实现的，一种是用奇异值分解去实现的。在上篇文章中便是基于特征值分解的一种解释。特征值和奇异值在大部分人的印象中，往往是停留在纯粹的数学计算中。而且线性代数或者矩阵论里面，也很少讲任何跟特征值与奇异值有关的应用背景。奇异

特征值分解、奇异值分解（SVD）、主成分分析（PCA）

1、特征值分解（SVD）: A=Q∑Q−1 A=Q\sum Q^{-1} Q= [v1,v2,...] [v_1,v_2,...] ∑=⎡⎣⎢λ1000λ20

关于奇异值分解SVD很好的解释

上一次写了关于 PCA与LDA的文章，PCA的实现一般有两种，一种是用特征值分解去实现的，一种是用奇异值分解去实现的。在上篇文章中便是基于特征值分解的一种解释。特征值和奇异值在大部分人的印象中，往往是停留在纯粹的数学计算中。而且线性代数或者矩阵论里面，也很少讲任何跟特征值与奇异值有关的应用背景。奇异值分解是一个有着很明显的物理意义的一种方法，它可以将一个比较复杂的矩阵用更小更简单的