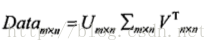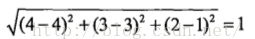《机器学习实战》笔记之十四—

本文主要是介绍《机器学习实战》笔记之十四——利用SVD简化数据，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第十四章利用SVD简化数据

14.1 SVD的应用

特点：

利用SVD能够用小得多的数据集来表示原始数据集。

优点：简化数据，去除噪声，提高算法的结果。

缺点：数据的转换可能难以理解。

隐性语义索引（LSI）

利用SVD的方法为隐性语义索引（Latent Semantic Indexing, LSI）或隐性语义分析（Latent Semantic Analysis, LSA）。在LSI中，一个矩阵是由文档和词语组成的，应用SVD时，会构建出多个奇异值，其代表了文档中的概念或主题。

推荐系统

上述矩阵由餐馆的菜和品菜师对这些菜的意见构成的。品菜师采用1到5之间的任意一个整数来对菜评级，如果品菜师没有尝过某道菜，则评级为0。对上述矩阵进行SVD分解，会得到两个奇异值（注意其特征值位2），也即仿佛有两个概念或主题与此数据集相关联。

14.2 矩阵分解

在很多情况下,数据中的一小段携带了数据集中的大部分信息,其他信息则要么是噪声,要么就是毫不相关的信息。在线性代数中还有很多矩阵分解技术。矩阵分解可以将原始矩阵表示成新的易于处理的形式。

SVD将原始数据集矩阵Data分解成三个矩阵U,sigma,V.T。

Figure 14-1: SVD矩阵分解公式

分解出来的sigma矩阵为对角阵，对角元素从大到小排列，称之为奇异值（Singular Value），这些奇异值为Data*Data.T特征值的平方根。且若是Data的秩为r，则奇异值的个数为r个，也即数据集中仅有r个重要特征。

14.3 利用python实现SVD

python numpy包里有linalg的线性代数工具箱，其有包括处理求范式、逆、行列式、伪逆、秩、qr分解、svd分解等等函数。

Figure 14-2: numpy linalg工具包

代码：

#!/usr/bin/env python
# coding=utf-8
from numpy import *
from numpy import linalg as la
def loadExData():return [[1,1,1,0,0],[2,2,2,0,0],[5,5,5,0,0],[1,1,0,2,2],[0,0,0,3,3],[0,0,0,1,1]]Data = loadExData()
U,Sigma,VT = la.svd(Data)
Sig3 = mat([[Sigma[0],0,0],[0,Sigma[1],0],[0,0,Sigma[2]]])#由于Sigma是以向量的形式存储，故需要将其转为矩阵，
#利用numpy的diag函数，直接Sig3 = np.diag(Sigma)[:3,:3]即可，diag将行向量转为矩阵，值放在对角线上,并取前面3行3列
print Sigma
print U[:,:3]*Sig3*VT[:3,:]#重构原始矩阵

结果：

Figure 14-3: sigma及重构后的矩阵

保留奇异值的数目：

保留矩阵中90%的能量信息。将所有的奇异值求平方和，将奇异值平方和累加到总值的90%为止。
保留上万奇异值中的前面2000到3000个。

14.4 基于协同过滤的推荐引擎

协同过滤通过将用户和其他用户的数据进行对比来实现推荐的。

当知道了两个用户或者两个物品之间的相似度，我们就可以利用已有的数据来预测未知的用户喜好。

唯一所需要的数学方法就是相似度的计算。

相似度计算：

Figure 14-4: 用于展示相似度计算的简单矩阵

手撕猪肉与鳗鱼饭的欧式距离：

相似度化为0到1之间：相似度=1/(1+距离)。

皮尔逊相关系数（Pearson correlation）：

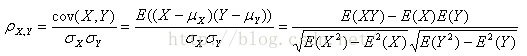
由numpy包中corrcoef()函数计算，化为0到1之间：0.5+0.5*corrcoef()。

余弦相似度（cosine similarity）：

coding:

#!/usr/bin/env python
# coding=utf-8
from numpy import *
from numpy import linalg as la
def loadExData():return [[1,1,1,0,0],[2,2,2,0,0],[5,5,5,0,0],[1,1,0,2,2],[0,0,0,3,3],[0,0,0,1,1]]def eulidSim(inA, inB):return 1.0/(1.0+la.norm(inA - inB))#根据欧式距离计算相似度def pearsSim(inA, inB):if len(inA)<3:return 1.0else:return 0.5+0.5*corrcoef(inA, inB, rowvar = 0)[0][1]def cosSim(inA, inB):num   = float(inA.T*inB)            #向量inA和向量inB点乘,得cos分子denom = la.norm(inA)*la.norm(inB)   #向量inA,inB各自范式相乘，得cos分母return 0.5+0.5*(num/denom)          #从-1到+1归一化到[0,1]myMat = mat(loadExData())
print eulidSim(myMat[:,0], myMat[:,4])#第一行和第五行欧式距离
print eulidSim(myMat[:,0], myMat[:,0])#第一行和第一行欧式距离
print cosSim(myMat[:,0], myMat[:,4])#第一行和第五行cos距离
print cosSim(myMat[:,0], myMat[:,0])#第一行和第一行cos距离
print pearsSim(myMat[:,0], myMat[:,4])#第一行和第五行皮尔逊距离
print pearsSim(myMat[:,0], myMat[:,0])#第一行和第一行皮尔逊距离

Figure 14-5: 三种距离度量的结果

基于物品的相似度还是基于用户的相似度

行与行之间比较的是基于用户的相似度，列与列之间比较的则是基于物品的相似度。基于物品相似度计算的时间会随物品数量的增加而增加，基于用户的相似度计算的时间则会随用户数量的增加而增加。如果用户的数目很多，那么我们可能倾向于使用基于物品相似度的计算方法。对于大部分产品导向的推荐系统而言，用户的数量往往大于物品的数量，即购买商品的用户数会多于出售的商品种类。

推荐系统的评价

我们将某些已知的评分值去掉，然后对它们进行预测，最后计算预测值与真实值之间的差异。通常使用的指标为最小均方根误差（Root Mean Squared Error, RMSE）。

14.5 示例：餐馆菜肴推荐引擎

推荐未尝过的菜肴

过程：给定一个用户，系统会为此用户返回N个最好的推荐菜。需要：

寻找用户没有评级的菜肴，即在用户-物品矩阵中的0值。
在用户没有评级的所有物品中，对每个物品预计一个可能的评级分数。
对这些物品的评分从高到低进行排序，返回前N个物品。
coding:

#===============基于物品相似度的推荐系统===============================
def standEst(dataMat, user, simMeas, item):     #数据矩阵，用户编号，相似度计算方法，物品编号n = shape(dataMat)[1]                       #行为用户，列为物品，n即物品数目simTotal    = 0.0ratSimTotal = 0.0for j in range(n):userRating = dataMat[user, j]           #j为某个物品编号if userRating == 0:continueelse:#寻找两个用户都评级的物品overLap = nonzero(logical_and(dataMat[:, item].A>0, dataMat[:,j].A>0))[0]#为向量if len(overLap)== 0:similarity = 0else:similarity = simMeas(dataMat[overLap, item], dataMat[overLap, j])simTotal += similarityratSimTotal += similarity * userRatingif simTotal == 0:return 0else:return ratSimTotal/simTotaldef recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):#输入用户编号，返回用户对前N个未评级物品预测评分值unratedItems = nonzero(dataMat[user, :].A==0)[1]                    #寻找未评级的物品，nonzero()[1]返回参数的某些为0的列的编号，dataMat中用户user对某个商品评价为0的列if len(unratedItems) == 0:return "you rated everything"else:itemScores = []for item in unratedItems:estimatedScore = estMethod(dataMat, user, simMeas, item)#对未评价的物品item进行进行预测评分，传入函数standEstitemScores.append((item,estimatedScore))return sorted(itemScores, key=lambda e:e[1], reverse = True)[:N]#前N个未评级物品myMat = mat(loadExData())
myMat[0,3] = myMat[0,4] = myMat[1,4] = myMat[2,3] = 4
myMat[4,1] = 2
print myMat
print recommend(myMat, 4)
print recommend(myMat, 4,simMeas = eulidSim)
print recommend(myMat, 4,simMeas = pearsSim)

效果：

Figure 14-6: 对用户4未评分的物品用不同的具体推荐的结果

利用SVD进提高推荐的效果

计算在奇异值的总能量，了解其到底需要多少维特征。

def loadExData2():return [[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],[0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],[0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],[3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],[5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],[0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],[4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],[0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],[0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],[0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],[1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]U,Sigma,VT = la.svd(mat(loadExData2()))
print Sigma
Sig2 =  Sigma**2
print Sig2
print sum(Sig2)*0.9
print sum(Sig2[:2])
print sum(Sig2[:3])

Figure 14-7: 奇异值的能量计算

前3个元素所包含的能量超过总能量的90%，故可以将这个11维的矩阵转换为3维矩阵。

对转换后的三维空间构造出一个相似度计算函数。利用SVD将所有的菜肴映射到一个低维空间。

#======================基于SVD的评分估计==========================
def SVDEst(dataMat, user, simMeas, item):n = shape(dataMat)[1]simTotal = 0.0ratSimTotal = 0.0U, Sigma, VT = la.svd(dataMat)Sig4 = mat(eye(4)*Sigma[:4]) #化为对角阵，或者用linalg.diag()函数可破xformedItems = dataMat.T*U[:,:4]*Sig4.I#构造转换后的物品for j in range(n):userRating = dataMat[user,j]if userRating == 0 or j == item:continueelse:similarity = simMeas(xformedItems[item,:].T, xformedItems[j, :].T)print "the %d and %d similarity is: %f" %(item,j,similarity)simTotal += similarityratSimTotal += similarity*userRatingif simTotal ==0 :return 0else:return ratSimTotal/simTotalmyMat = mat(loadExData2())
print recommend(myMat, 1, estMethod = SVDEst)
print recommend(myMat, 1, estMethod = SVDEst, simMeas = pearsSim)

Figure 14-8：使用SVD评分估计

14.6 示例：基于SVD的图像压缩

原始图像为32×32=1024像素的图像，用SVD对其进行压缩，以节省空间或带宽开销。

coding:

def printMat(inMat, thresh=0.8):for i in range(32):for k in range(32):if float(inMat[i,k]) > thresh:print 1,else:print 0,print ""def imgCompress(numSV=3, thresh=0.8):myl = []for line in open("0_5.txt").readlines():newRow = []for i in range(32):newRow.append(int(line[i]))myl.append(newRow)myMat = mat(myl)print "****original matrix****"printMat(myMat,thresh)U, Sigma, VT = la.svd(myMat)SigRecon = mat(zeros((numSV, numSV)))for k in range(numSV):SigRecon[k,k] = Sigma[k]reconMat = U[:,:numSV]*SigRecon*VT[:numSV,:]#重构矩阵print "****reconstructed matrix using %d singular values****" % numSVprintMat(reconMat, thresh)print imgCompress(2)

效果：