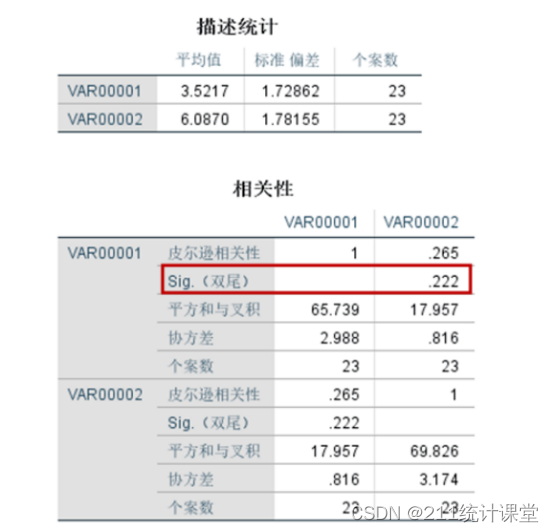
pearson专题

平方Pearson相关系数（SPCC）相关公式的推导

1、PCC及SPCC的定义最近推导了维纳滤波的公式，其中最重要的是当然是最小平方误差准则（MSE）。但是在很多实际应用中，参考信号是不可知的，因此MSE准则不具有实际意义。为了解决这个问题，我们需要寻找另一个准则替代MSE成为新的代价函数。这就是皮尔逊相关系数（Pearson Correlation Coefficient, PCC）的来历。通过研究发现，相较于MSE，PCC具有许多吸引人的优

【Python】豆瓣电影TOP250数据规律分析（Pearson相关系数、折线图、条形图、直方图）

1、数据集预览部分数据说明：豆瓣排名num 评分rating_num 评分人数comment_num 电影时长movie_duration 2、查看电影数据集基本数据信息 import numpy as npimport pandas as pdimport matplotlib.pyplot as pltdata = pd.read_csv('电影排名.csv') #读取数据#

数学建模：数据相关性分析（Pearson和 Spearman相关系数）含python实现

相关性分析是一种用于衡量两个或多个变量之间关系密切程度的方法。相关性分析通常用于探索变量之间的关系，以及预测一个变量如何随着另一个变量的变化而变化。在数学建模中，这是常用的数据分析手段。相关性分析的结果通常用相关系数来表示，相关系数的取值范围为-1到1，其中1表示完全正相关，-1表示完全负相关，0表示没有相关性。我们常用的相关系数包括： Pearson相关系数：用于衡量两个连续变量之

python统计分析——协方差和pearson相关系数

参考资料：用python动手学统计学使用数据见代码： dic={"x":[18.5,18.7,19.1,19.7,21.5,21.7,21.8,22.0,23.4,23.8],"y":[34,39,41,38,45,41,52,44,44,49]}cov_data=pd.DataFrame(dic) 变量x、y的协方差Cov(x,y)的计算公式如下：协方差的含义：协方差大于

Pearson、Spearman 相关性分析使用

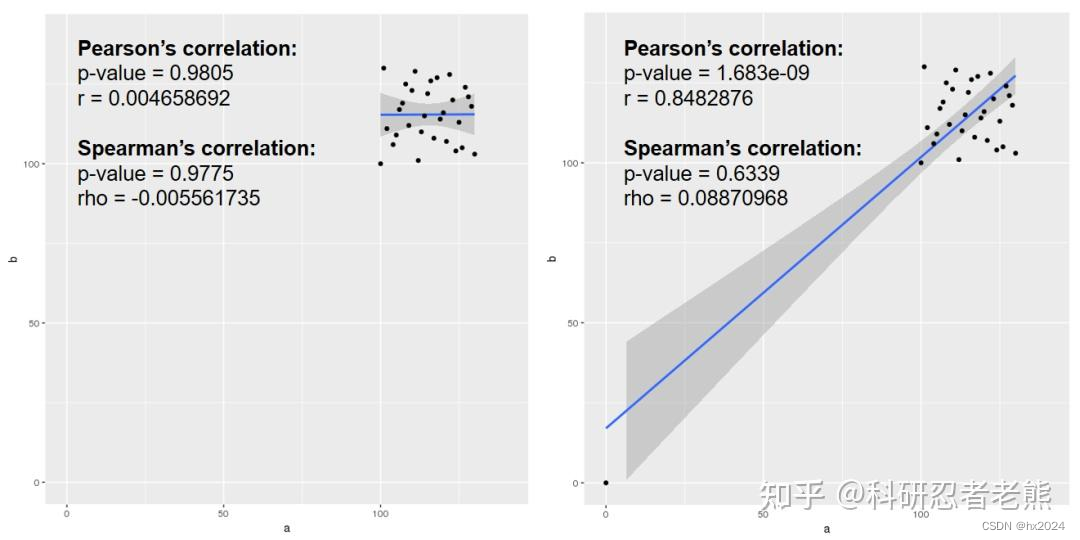
介绍 Pearson 积差相关系数衡量了两个定量变量之间的线性相关程度。用来衡量两个数据集的线性相关程度，仅当一个变量的变化与另一个变量的比例变化相关时，关系才是线性的。 Spearman等级相关系数则衡量分级定序变量之间的相关程度。斯皮尔曼相关系数不关心两个数据集是否线性相关，而是单调相关。它是基于每个变量的排名值，而不是原始数据，所以斯皮尔曼相关也叫等级相关或者秩相关（即rank）。

PKD: General Distillation Framework for Object Detectors via Pearson Correlation Coefﬁcient阅读笔记

(一) Title 论文地址:https://arxiv.org/abs/2207.02039 (二) Summary 研究背景：在目标检测任务中KD发挥着压缩模型的作用，但是对于heterogeneous detectors(异构)之间的蒸馏仍然lack of study。本文的主要工作来自异构教师的FPN feature能够帮助具有不同detect head和label ass

[论文阅读]PKD——基于Pearson相关系数的目标检测器通用蒸馏框架

PKD General Distillation Framework for Object Detectors via Pearson Correlation Coefficient 基于Pearson相关系数的目标检测器通用蒸馏框架论文网址：PKD 创新点 1.提出FPN特征模仿适用于异构检测器对。之前的工作大多只考虑同质检测器对,很少研究异构情况。 2.指出直接最小化特征图之间的均方误

论文阅读——《A new combination method based on Pearson coefficient and information entropy for multi-sens》

文章目录前言一、DS证据理论合成规则计算二、论文提出的方法的计算过程1、构造相关矩阵，并对其进行修正。2、计算两个BBA之间的证据距离，并构造evidence distance matrix D（证据距离矩阵）。3、计算证据 m i m_{i} mi和其他证据之间的距离4、计算证据 m i m_{i} mi 的可信度水平 C r d Crd Crd，并作归一化 C r d ~

统计学三大相关系数之皮尔森（pearson）相关系数

统计相关系数简介统计学的相关系数经常使用的有三种:皮尔森（pearson）相关系数和斯皮尔曼（spearman）相关系数和肯德尔（kendall）相关系数.皮尔森相关系数是衡量线性关联性的程度，p的一个几何解释是其代表两个变量的取值根据均值集中后构成的向量之间夹角的余弦. 相关系数：考察两个事物（在数据里我们称之为变量）之间的相关程度。如果有两个变量：X、Y，最终计算出的相关系数的含义可

【NCC】之一：从Pearson相关系数到模板匹配的NCC方法

文章目录 <center> NCC(Normalized Cross Correlation)1.**Pearson相关系数**2.**协方差 covariance**3. **方差 variance**4.模板匹配中的NCC方法5.实现过程6.测试结果7.部分核心源码NCC.cpp NCC(Normalized Cross Correlation) 从Pearson相关

Pearson correlation皮尔逊相关性分析

在参数检验的相关性分析方法主要是皮尔逊相关（Pearson correlation）。既然是参数检验方法，肯定是有一些前提条件。皮尔逊相关的前提是必须满足以下几个条件：变量是连续变量；比较的两个变量必须来源于同一个总体；没有异常值；两个变量都符合正态分布。正态分布的呈现是倒“U”型曲线。在实际分析过程中，想要一份数据同时满足以上条件，确实是有一定难度的。毕竟我们是没法保证收上来的数