本文主要是介绍PKD: General Distillation Framework for Object Detectors via Pearson Correlation Coefficient阅读笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
(一) Title

论文地址:https://arxiv.org/abs/2207.02039
(二) Summary
研究背景:
- 在目标检测任务中KD发挥着压缩模型的作用,但是对于heterogeneous detectors(异构)之间的蒸馏仍然lack of study。
本文的主要工作
- 来自异构教师的FPN feature能够帮助具有不同detect head和label assignment方式的学生.这里给我的感觉是使用anchor-based框架也能够蒸馏anchor-free的框架
- 引入了皮尔逊相关系数来进行蒸馏实现relax constraints
本文的主要贡献:
- 使用Pearson Correlation Coefficient对于同质和异质的教师-学生蒸馏结构同样有帮助,并且收敛更快
- MaskRCNN-Swin detector作为教师模型,ResNet-50 based RetinaNet
and FCOS achieve 41.5% and 43.9% mAP on COCO2017。
(三) Problem Statement
作者指出直接对齐学生网络和教师网络的特征存在着两个问题:
- 学生网络和教师网络feature magnitude(特征幅度之间的差异)会导致over strict constraint。蒸馏任务中有没有什么方法能够衡量特征语义之间的差异呢?
- 在FPN和具有较大特征幅度的feature layer中,很容易把控住梯度的收敛方向,从而引入更多的噪声进来
从图片展示上来看,如下:
- 上图中左图应该是按照特征激活值所在区间绘制了一个柱状图这里纵坐标上角标单位是 1 e 6 1e6 1e6,应该统计的是FPN的所有特征层,从横坐标上来看,是直接对特征图的值按照取值大小划分区间,对在该区间内的特征点数量进行的统计。
- 中间图的公式略微有点儿难看懂, number i = ∑ u , v 1 [ arg max c s u , v ( c ) = i ] \text { number }_{i}=\sum_{u, v} \mathbb{1}\left[\arg \max _{c} s_{u, v}^{(c)}=i\right] number i=∑u,v1[argmaxcsu,v(c)=i],首先这里的 number i \text { number }_{i} number i表示的是纵坐标的取值,图中横坐标表示特征图P3的通道数,然后里面的 1 [ arg max c s u , v ( c ) = i ] \mathbb{1}\left[\arg \max _{c} s_{u, v}^{(c)}=i\right] 1[argmaxcsu,v(c)=i]表示的是对于第 i i i个通道,如果 ( u , v ) (u,v) (u,v)位置对应的特征取值为所有通道中最大的那个,则取值为1,否则取值为0.由于第 l l l个FPN层的特征为 s l ∈ R C × H × W \boldsymbol{s}_{\boldsymbol{l}} \in \mathbb{R}^{C \times H \times W} sl∈RC×H×W,取最大值来压缩通道数量得到2D的特征图表示。实际上这里统计的是2D特征图上的特征分别来自哪个特征通道,即哪一个特征通道相对来说更加重要。从这个图中我们也可以看到总有一些特征通道的激活值比其他通道大,然而less activated features在蒸馏任务中同样关键,这部分对应的梯度较小
- 最右侧图是对2D图进行0-255归一化之后的可视化图片。这里考虑的是不同stage之间特征的差异问题,上面那组图为教师模型,下为学生模型,教师P6的特征激活值要比P3小很多,从而导致具有较大激活值的stage在梯度反向传播中更加关键,占据更大的梯度向量,此外在同背景无关的位置可视化特征图上也出现了具有较大激活值,这些位置对于蒸馏任务来说会额外的引入噪声。
从上面的描述中,总结下来,希望能够解决的三个问题是:
- FPN不同stage之间特征magnitude差异
- 在文献[34,46]中给出的less activated features are still practical for distillation假设成立的条件下,这里博主对于这个假设持怀疑态度,从之前的论文和实验经历来看,较大激活值的特征在蒸馏过程中能够起到更大的帮助,再加上这个假设也就相当于所有的activation均有用,这个结论并不是很赞同,如何处理具有less activated feature的特征通道?
- 对于非object位置的large magnitude如何避免其引入的额外噪声?
(四) Method
本文提出使用Pearson Correlation Coefficient(PCC)来进行蒸馏,为了解决上述3个问题negative influences of magnitude difference, dominant FPN stages and channels,首先将特征图归一化到0均值,单位方差。这里使用的是哪一个norm方式呢?这里实际上等价于最大化皮尔逊相关系数,此外PCC还能够减少特征幅度对于梯度反传的影响。使得训练过程更加稳定。这里需要注意的是:仅仅对于FPN特征进行了蒸馏。
详细的蒸馏过程如下:
- 首先,对特征图进行0均值,unit 方差的归一化,具体的方式为:
一个mini-batch的特征图的batch大小为 b b b,特征图size为 h w hw hw,令 m = ∥ B ∥ = b ⋅ h w m=\|\mathbb{B}\|=b \cdot h w m=∥B∥=b⋅hw, s ( c ) ∈ R m \boldsymbol{s}^{(c)} \in \mathbb{R}^{m} s(c)∈Rm为mini-batch第 c c c个通道的FPN输出,最终得到归一化的学生和教师网络的特征值: s ^ 1 … m \hat{s}_{1 \ldots m} s^1…m和 t ^ 1 … m \hat{t}_{1 \ldots m} t^1…m。这里的均值和方差的计算方式感觉就是做了一个BN啊!!!- 对应的蒸馏损失函数为:
L F P N = 1 2 m ∑ i = 1 m ( s ^ i − t ^ i ) 2 \mathcal{L}_{F P N}=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{s}_{i}-\hat{t}_{i}\right)^{2} LFPN=2m1i=1∑m(s^i−t^i)2
最大化皮尔逊相关系数的表示方式为:
对应到文中的表达形式为:
r ( s , t ) = ∑ i = 1 m ( s i − μ s ) ( t i − μ t ) ∑ i = 1 m ( s i − μ s ) 2 ∑ i = 1 m ( t i − μ t ) 2 r(\boldsymbol{s}, \boldsymbol{t})=\frac{\sum_{i=1}^{m}\left(s_{i}-\mu_{s}\right)\left(t_{i}-\mu_{t}\right)}{\sqrt{\sum_{i=1}^{m}\left(s_{i}-\mu_{s}\right)^{2}} \sqrt{\sum_{i=1}^{m}\left(t_{i}-\mu_{t}\right)^{2}}} r(s,t)=∑i=1m(si−μs)2∑i=1m(ti−μt)2∑i=1m(si−μs)(ti−μt)
这里 s ^ , t ^ ∼ N ( 0 , 1 ) \hat{\boldsymbol{s}}, \hat{\boldsymbol{t}} \sim \mathcal{N}(0,1) s^,t^∼N(0,1)服从标准正态分布,并且有 1 m − 1 ∑ i s ^ i 2 = 1 , 1 m − 1 ∑ i t ^ i 2 = 1 \frac{1}{m-1} \sum_{i} \hat{s}_{i}^{2}=1, \frac{1}{m-1} \sum_{i} \hat{t}_{i}^{2}=1 m−11∑is^i2=1,m−11∑it^i2=1成立,此时上述的损失函数就变成了:
L F P N = 1 2 m ( ( 2 m − 2 ) − 2 ∑ i = 1 m s ^ i t ^ i ) = 2 m − 2 2 m ( 1 − r ( s , t ) ) ≈ 1 − r ( s , t ) \begin{aligned} \mathcal{L}_{F P N} &=\frac{1}{2 m}\left((2 m-2)-2 \sum_{i=1}^{m} \hat{s}_{i} \hat{t}_{i}\right) \\ &=\frac{2 m-2}{2 m}(1-r(\boldsymbol{s}, \boldsymbol{t})) \approx 1-r(\boldsymbol{s}, \boldsymbol{t}) \end{aligned} LFPN=2m1((2m−2)−2i=1∑ms^it^i)=2m2m−2(1−r(s,t))≈1−r(s,t)
即最小化损失等价于最大化皮尔逊相关系数。此时对于损失对于FPN特征输出 s i s_i si的梯度为:
∂ L F P N ∂ s i = 1 m σ s ( s i ^ ⋅ r ( s , t ) − t i ^ ) \frac{\partial \mathcal{L}_{F P N}}{\partial s_{i}}=\frac{1}{m \sigma_{s}}\left(\hat{s_{i}} \cdot r(\boldsymbol{s}, \boldsymbol{t})-\hat{t_{i}}\right) ∂si∂LFPN=mσs1(si^⋅r(s,t)−ti^)
这里梯度计算为什么为多了一个 r ( s , t ) r(\boldsymbol{s}, \boldsymbol{t}) r(s,t)呢?首先 L F P N = 1 2 m ∑ i = 1 m ( s ^ i − t ^ i ) 2 \mathcal{L}_{F P N}=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{s}_{i}-\hat{t}_{i}\right)^{2} LFPN=2m1∑i=1m(s^i−t^i)2, s ^ i = s i − μ s σ s \hat{s}_{i}=\frac{s_{i}-\mu_s}{\sigma_s} s^i=σssi−μs, L F P N \mathcal{L}_{F P N} LFPN直接对 s i s_{i} si求导,从这里看应该是 ∂ L F P N ∂ s i = 1 m σ s ( s i ^ − t i ^ ) \frac{\partial \mathcal{L}_{F P N}}{\partial s_{i}}=\frac{1}{m \sigma_{s}}\left(\hat{s_{i}}-\hat{t_{i}}\right) ∂si∂LFPN=mσs1(si^−ti^)吧?没看出来是怎么引入皮尔逊相关系数的
从上述的梯度表达式中可以看出,皮尔逊系数对于学生网络激活输出进行了加权,从加权结果中来看,实际上这里假设不相关,然后 r ( s , t ) = 0 r(\boldsymbol{s}, \boldsymbol{t})=0 r(s,t)=0,此时梯度完全收教师网络值把控?梯度并不为0,整体给我的感觉很奇怪!,除了这个地方之外,关于皮尔逊相关系数对于上述三个问题的解决描述不清楚
最终的总损失表示为:
L = L G T + α L F P N \mathcal{L}=\mathcal{L}_{G T}+\alpha \mathcal{L}_{F P N} L=LGT+αLFPN
PCC和KL散度之间的关联是什么呢?
KL散度在蒸馏过程中的处理方式为:首先通过softmax函数将激活值转换成概率分布,然后最小化教师和学生激活值之间的KL散度损失,从公式上来看是:
L K L = T 2 ∑ i = 1 m ϕ ( t i ) ⋅ log [ ϕ ( t i ) ϕ ( s i ) ] \mathcal{L}_{K L}=T^{2} \sum_{i=1}^{m} \phi\left(t_{i}\right) \cdot \log \left[\frac{\phi\left(t_{i}\right)}{\phi\left(s_{i}\right)}\right] LKL=T2i=1∑mϕ(ti)⋅log[ϕ(si)ϕ(ti)]
归一化方式为:
ϕ ( t ) = exp ( t i / T ) ∑ j = 1 m exp ( t j / T ) \phi(t)=\frac{\exp \left(t_{i} / T\right)}{\sum_{j=1}^{m} \exp \left(t_{j} / T\right)} ϕ(t)=∑j=1mexp(tj/T)exp(ti/T)
然后,这里作者说在高温条件下,最小化post-normalized features之间的KL散度,等价于最小化MSE,然后就等价于在pre-normalized features之间的最大化皮尔逊相关系数。
接着KL散度对于normalized activation s ^ i \hat{s}_i s^i求梯度,得到:
∂ L K L ∂ s ^ i = T ( q i − p i ) = T ( e s i / T ^ ∑ j e s j / T ^ − e t i / T ^ ∑ j e t j / T ^ ) \frac{\partial \mathcal{L}_{K L}}{\partial \hat{s}_{i}}=T\left(q_{i}-p_{i}\right)=T\left(\frac{e^{\hat{s_{i} / T}}}{\sum_{j} e^{\hat{s_{j} / T}}}-\frac{e^{\hat{t_{i} / T}}}{\sum_{j} e^{\hat{t_{j} / T}}}\right) ∂s^i∂LKL=T(qi−pi)=T(∑jesj/T^esi/T^−∑jetj/T^eti/T^)
其中 p i = ϕ ( t i ^ ) and q i = ϕ ( s i ^ ) p_{i}=\phi\left(\hat{t_{i}}\right) \text { and } q_{i}=\phi\left(\hat{s_{i}}\right) pi=ϕ(ti^) and qi=ϕ(si^),这里的梯度求导方式不知道是则得到的?
接着当温度足够高时,有近似计算如下:
∂ L K L ∂ s i ^ ≈ T ( 1 + s i ^ / T N + ∑ j s j ^ / T − 1 + t i ^ / T N + ∑ j t j ^ / T ) \frac{\partial \mathcal{L}_{K L}}{\partial \hat{s_{i}}} \approx T\left(\frac{1+\hat{s_{i}} / T}{N+\sum_{j} \hat{s_{j}} / T}-\frac{1+\hat{t_{i}} / T}{N+\sum_{j} \hat{t_{j}} / T}\right) ∂si^∂LKL≈T(N+∑jsj^/T1+si^/T−N+∑jtj^/T1+ti^/T)
由于 s ^ i , t ^ i \hat{s}_i,\hat{t}_i s^i,t^i都是0均值的,然后上式就可以简化成:
∂ L K L ∂ s i ^ ≈ 1 N ( s i ^ − t i ^ ) \frac{\partial \mathcal{L}_{K L}}{\partial \hat{s_{i}}} \approx \frac{1}{N}\left(\hat{s_{i}}-\hat{t_{i}}\right) ∂si^∂LKL≈N1(si^−ti^)
然后观察同PCC之间的差异。
(五) Experiments

同质结构下的蒸馏
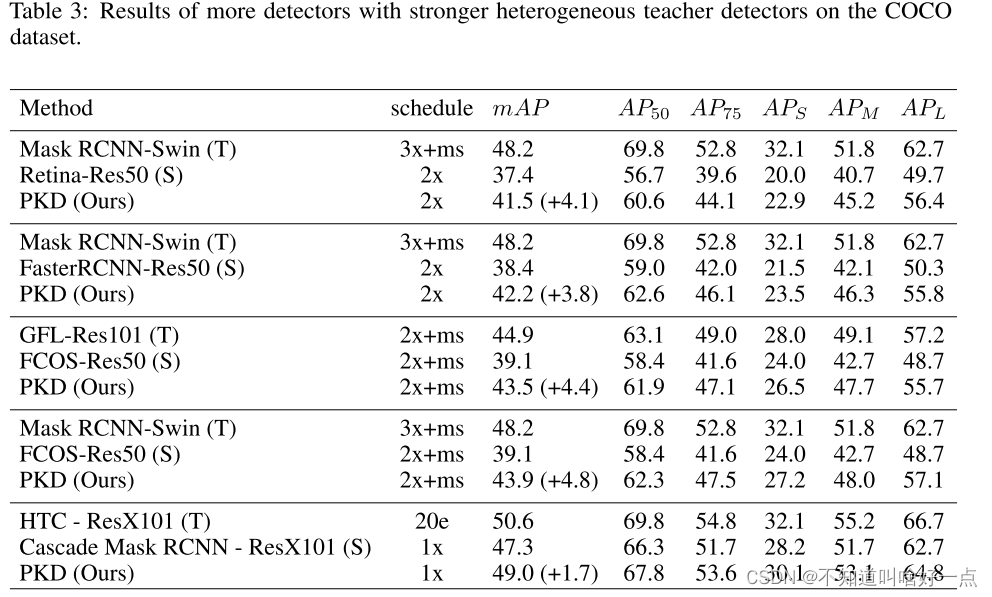
异质结构下的蒸馏过程。

针对之前提到的三种问题,设计了三个蒸馏对象来比较MSE和本文提出的PKD的差异。

超参数对于蒸馏效果的影响
这篇关于PKD: General Distillation Framework for Object Detectors via Pearson Correlation Coefficient阅读笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!










