本文主要是介绍Pearson correlation皮尔逊相关性分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在参数检验的相关性分析方法主要是皮尔逊相关(Pearson correlation)。既然是参数检验方法,肯定是有一些前提条件。皮尔逊相关的前提是必须满足以下几个条件:
- 变量是连续变量;
- 比较的两个变量必须来源于同一个总体;
- 没有异常值;
- 两个变量都符合正态分布。
正态分布的呈现是倒“U”型曲线。在实际分析过程中,想要一份数据同时满足以上条件,确实是有一定难度的。毕竟我们是没法保证收上来的数据,一定恰好是符合正态分布的。
皮尔逊相关系数的范围是位于[-1,1]之间。相关系数展示了方向性:
- 如果相关系数接近1,说明两个变量之间呈较高的正相关性;
- 如果相关系数接近-1,说明两个变量之间呈较高的负相关性;
- 如果相关系数接近0,说明两个变量之间彼此独立,没有相关性。
皮尔逊相关的结果包括两个值,相关系数和P值。在相关性分析中,P值代表着两个变量是否显著相关。
一般而言,分析结果里,我们先看P值。如果P值小于0.05,那么两个变量呈显著的相关性。
然后再看相关系数的方向性,报告两个变量是显著的正相关或负相关。
SPSS操作详细步骤
第一步,选择“分析”——“相关”——“双变量”。
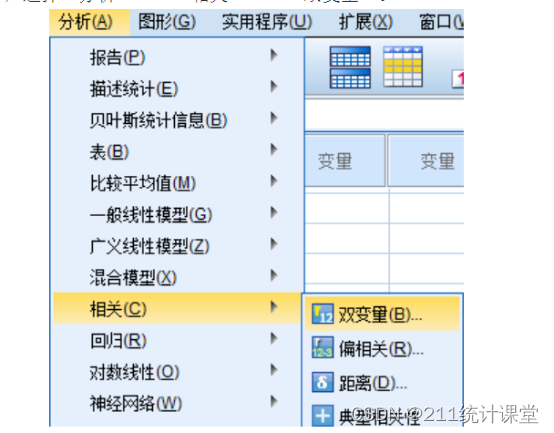
第二步,在相关系数里,选择“皮尔逊”。显著性可以选“双侧”。
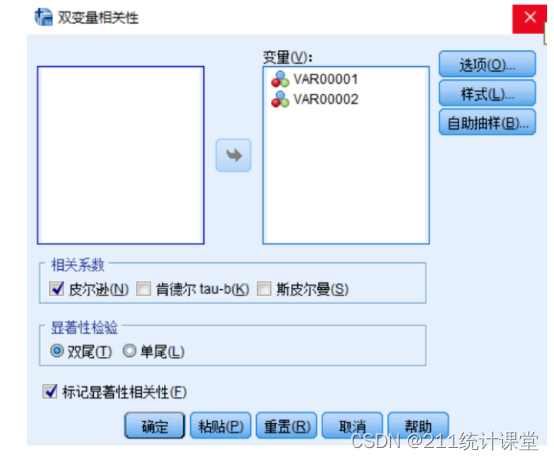
第三步,点击“选项”,可以勾选统计,计算平均数与标准差等,如下图所示。
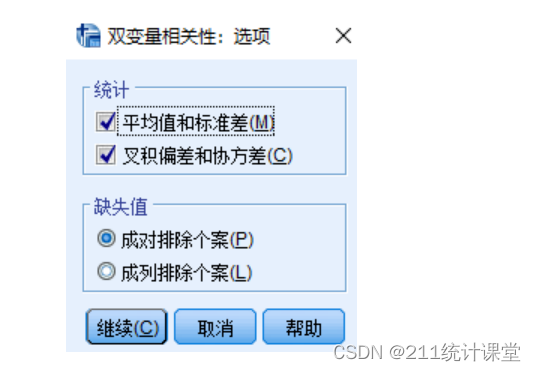
其他设置都可以默认。直接点“确定”,就能生成结果了。
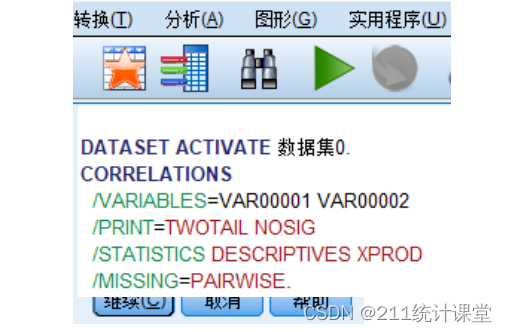
如果想要保留SPSS语法文件,可以先点击“粘贴”,保存本次所有操作,如图5.4所示。下次还要执行同样的操作,直接全选以后,点击绿色小三角符号,就可以生成皮尔逊分析结果了。
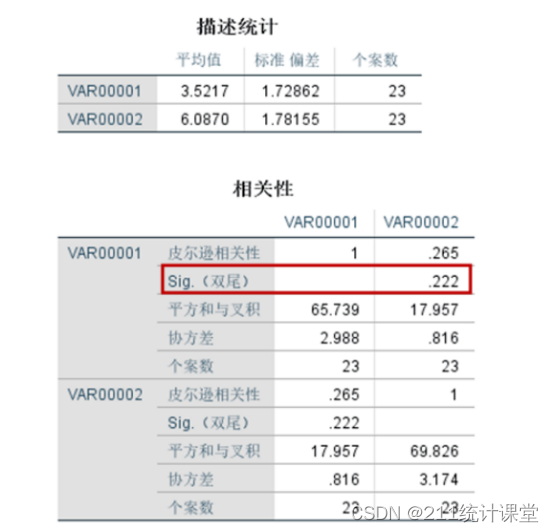
皮尔逊相关性分析结果显示,P值显著性为0.222,如红框中所示。P值大于0.05,说明示例的两个变量无显著相关性。相关性系数为0.265,离1比较远,也说明相关性不高。
以上就是皮尔逊相关性分析的内容。
这篇关于Pearson correlation皮尔逊相关性分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





