nearest专题
Leetcode 3275. K-th Nearest Obstacle Queries
Leetcode 3275. K-th Nearest Obstacle Queries 1. 解题思路2. 代码实现 题目链接:3275. K-th Nearest Obstacle Queries 1. 解题思路 这一题的话其实逻辑上非常简单,就是维护一个距离的有序数组,不断取第k大的元素即可。 不过好死不死的题目设置成只要这么干就一定超时,因此我们不得不想办法去优化算法复杂度,但说白
python K-Nearest Neighbor KNN算法
1、最初的邻近算法,分类算法,基于实例的学习,懒惰学习。 2、算法步骤: a、为了判断未知实例类别,选择所有已知的实例作为参考 b,选择参数k c,计算未知实例和所有已知实例的距离 d,选择最近k个已知实例 e,根据少数服从多数,让未知实例归类为k个中最多的类别 公式:E(x,y)=(xi-yi)^2求和之后再开方 import mathdef ComputeEuclidean
【机器学习】K近邻(K-Nearest Neighbors,简称KNN)的基本概念以及消极方法和积极方法的区别
引言 K近邻(K-Nearest Neighbors,简称KNN)算法是一种基础的机器学习方法,属于监督学习范畴 文章目录 引言一、K近邻(K-Nearest Neighbors,简称KNN)1.1 原理详述1.1.1 距离度量1.1.2 选择k值1.1.3 投票机制 1.2 实现步骤1.3 参数选择1.4 应用场景1.5 优缺点1.5.1 优点1.5.2 缺点 1.6 k-近邻代
Educational Codeforces Round 1C. Nearest vectors(极角排序+long double 精度)
题目链接 题意:给你一堆的向量,问你向量之间的夹角最小的是那一对。 解法:极角排序,然后枚举相邻的一对就可以啦,但是坑爹的是double精度不够,使用long double 读入使用cin。。。 #include<bits/stdc++.h>using namespace std;#define LL long long#define pb push_back#define X f
poj 1330 Nearest Common Ancestors(LCA模板)
http://poj.org/problem?id=1330 题意:给出两个点,求出这两个点最近的公共祖先。 求LCA的模板题。 大致思路就是访问到某个节点时,先将它自己加入集合中,然后递归访问它的子树,同时把子树加入到集合中来。子树搜索完毕后,判断该节点是否是输入的两个节点之一,若是,并且另外一个也已标记为访问过,那么另外一个节点的祖先便是他们的LCA。 #include<stdio
深入第一个机器学习算法: K-近邻算法(K-Nearest Neighbors)
本篇博文主要涉及到以下内容: K-近邻分类算法从文本文件中解析和导入数据使用Matplotlib创建扩散图归一化数值 K-近邻算法 功能: 非常有效且易于掌握。 学习K-近邻算法的思路: 首先,探讨k-近邻算法的基本理论,以及如何使用距离测量的方法分类物品。其次,使用Python 从文本文件中导入并解析数据。再次,讨论当存在多种数据源时,如何避免计算距离时可能碰到的一些常见的错误。最后,
macos使用yarn创建vite时出现Usage Error: The nearest package directory问题
步骤是macos上使用了yarn create vite在window上是直接可以使用了yarn但是在macos上就出现报错 我们仔细看,它说的If /Users/chentianyu isn't intended to be a project, remove any yarn.lock and/or package.json file there.说是要我们清除yarn.lock
基于FPGA的数字信号处理(11)--定点数的舍入模式(2)向最临近值取整nearest
前言 在之前的文章介绍了定点数为什么需要舍入和几种常见的舍入模式。今天我们再来看看另外一种舍入模式:向最临近值取整nearest。 10进制数的nearest nearest: 向最临近值方向取整。它的舍入方式和四舍五入非常类似,都是舍入到最近的整数,比如1.75 nearest到2,-0.25 nearest到0等。二者唯一的区别在于对0.5这类数据的处理上。 0.5的round结果是1
用最近邻插值(Nearest Neighbor interpolation)进行图片缩放
图片缩放的两种常见算法: 最近邻域内插法(Nearest Neighbor interpolation) 双向性内插法(bilinear interpolation) 本文主要讲述最近邻插值(Nearest Neighbor interpolation算法的原理以及python实现 基本原理 最简单的图像缩放算法就是最近邻插值。顾名思义,就是将目标图像各点的像素值设为源图像
K Nearest Neighbor
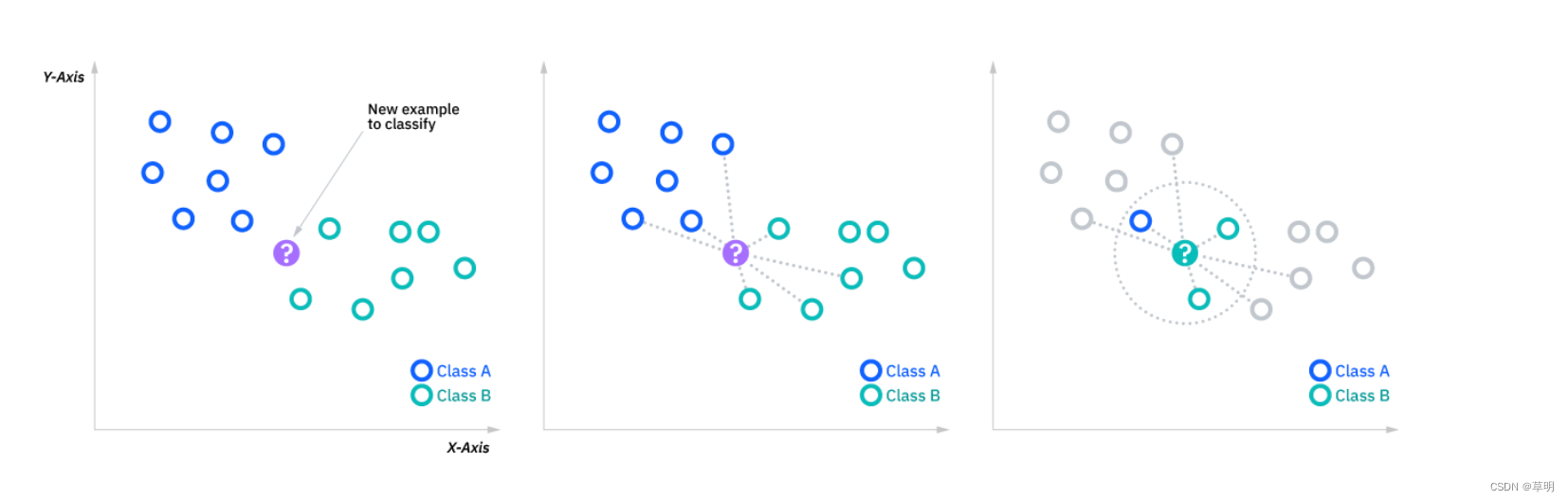
KNN算法 概述 KNN算法:即最邻近分类算法(K-NearestNeighbor 算法思路:如果一个样本在特征空间中的k个最相似(即特征空间中最临近)的样本中的大多数属于某一个类别 则该样本也属于这个类别 k通常是不大于20的整数 KNN算法中 所选择的邻居都是已经正确分类的对象 该方法在定义决策上只依据最邻近的一个或几个样本的类别来决定待分样本所属的类别 如上所示 绿色圆要被决定
【机器学习】KNN(K-Nearest Neighbor)
KNN简介 KNN算法又称为K最近邻分类(K-nearest neighbor classification)算法,是一种非常简单的机器学习分类算法。 KNN算法的原理十分简单:对于待分类的样本,计算其到所有训练样本的距离,从中选取K个距离最近的训练样本,统计这K个距离最近的训练样本所属的类别,按照少数服从多数的原理,将待分类的样本归入k个训练样本所属数目最
机器学习之深入理解K最近邻分类算法(K Nearest Neighbor)
【机器学习】《机器学习实战》读书笔记及代码:第2章 - k-近邻算法 1、初识 K最近邻分类算法(K Nearest Neighbor)是著名的模式识别统计学方法,在机器学习分类算法中占有相当大的地位。主要应用领域是对未知事物的识别,即推断未知事物属于哪一类。 推断思想是,基于欧几里得定理,推断未知事物的特征和哪一类已知事物的的特征最接近。简单来说就是:如果一个样本在特征空间中的k个最相似(
【机器学习】k近邻(k-nearest neighbor )算法
文章目录 0. 前言1. 算法原理1.1 距离度量1.2 参数k的选择 2. 优缺点及适用场景3. 改进和扩展4. 案例5. 总结 0. 前言 k近邻(k-nearest neighbors,KNN)算法是一种基本的监督学习算法,用于分类和回归问题。k值的选择、距离度量及分类决策规则是k近邻法的三个基本要素。 1. 算法原理 给定一个训练数据集,KNN算法通过计算待分类样本与
【理解机器学习算法】之Nearest Shrunken Centroid(纯Python)
从头开始实现最近缩小质心(NSC)分类器涉及理解它如何通过将质心缩小到所有类的总质心方向来修改基本的最近质心方法,有效地执行特征选择。这种方法特别是在微阵列预测分析(PAM)中的应用而闻名。这里,我们将概述算法的简化版本并提供一个基本的Python实现。 最近缩小质心算法的基本步骤 1. **计算质心**:计算训练数据中每个类的质心。 2. **计算总质心**:使用所有训练数据计算总质心,不论
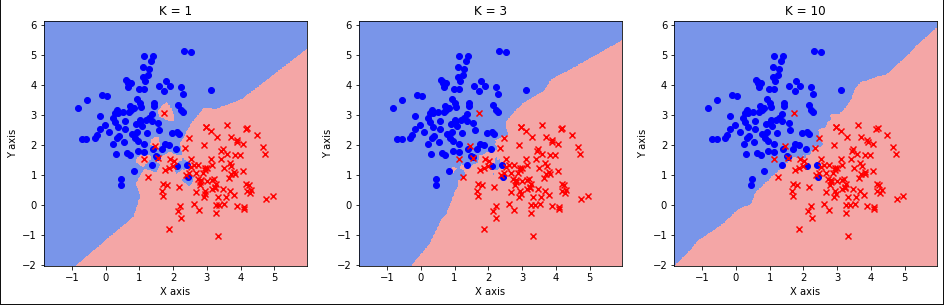
【k近邻】 K-Nearest Neighbors算法k值的选择
【k近邻】 K-Nearest Neighbors算法原理及流程 【k近邻】 K-Nearest Neighbors算法距离度量选择与数据维度归一化 【k近邻】 K-Nearest Neighbors算法k值的选择 【k近邻】 Kd树的构造与最近邻搜索算法 【k近邻】 Kd树构造与最近邻搜索示例 k近邻算法(K-Nearest Neighbors,简称KNN)是一种常用的监督学习算法,可
【k近邻】 K-Nearest Neighbors算法原理及流程
【k近邻】 K-Nearest Neighbors算法原理及流程 【k近邻】 K-Nearest Neighbors算法距离度量选择与数据维度归一化 k近邻算法(K-Nearest Neighbors,简称KNN)是一种常用的监督学习算法,可以用于分类和回归问题。在OpenCV中,KNN算法的函数为`cv.ml.KNearest_create()。 k近邻算法原理 K近邻
OpenCV(2)ML库-K-Nearest Neighbour分类器
KNN也是最邻近结点算法(k-Nearest Neighbor algorithm)的缩写形式,也可称为邻近算法。是电子信息分类器算法的一种。KNN方法对包容型数据的特征变量筛选尤其有效。 最邻近结点算法采用向量空间模型来分类,概念为相同类别的案例,彼此的相似度高,而可以借由计算与已知类别案例之相似度,来评估未知类别案例可能的分类。 目标:分类未知类别案例。 输入:待分类未知类别案
Nearest Neighbor Search 简单几何(求空间一点到区域的距离)
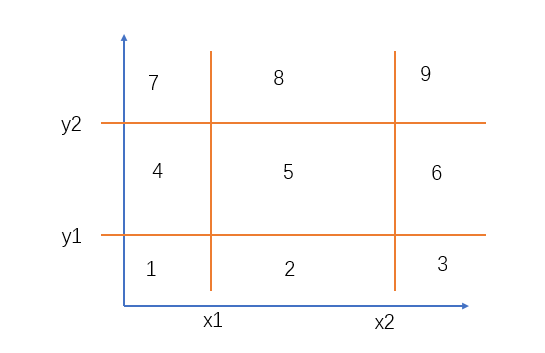
题目链接: https://acm.bnu.edu.cn/v3/statments/52296.pdf 题意: 求空间一点(x0,y0,z0),到三维空间区域的最小距离? 分析: 先求二维平面的最小距离(将平面分为9部分分别处理即可),再求高的距离。 AC代码: #include <iostream>#include <cstdio>#include <cstring>#i
POJ_1330 Nearest Common Ancestors
题意 求一棵树上的某两个节点的最近公共祖先。 思路 这是tarjan算法的例题,所以我这里用的是tarjan算法。 代码 #include<cstdio>#include<cstring>using namespace std;int f1,f2,p,q,t,n,m,x,y,root,tot,head[10001],v[10001],fa[10001];struct no
LeetCode //C - 1926. Nearest Exit from Entrance in Maze
1926. Nearest Exit from Entrance in Maze You are given an m x n matrix maze (0-indexed) with empty cells (represented as ‘.’) and walls (represented as ‘+’). You are also given the entrance of the ma
2.机器学习-K最近邻(k-Nearest Neighbor,KNN)分类算法原理讲解
2️⃣机器学习-K最近邻(k-Nearest Neighbor,KNN)分类算法原理讲解 个人简介一·算法概述二·算法思想2.1 KNN的优缺点 三·实例演示3.1电影分类3.2使用KNN算法预测 鸢(yuan)尾花 的种类3.3 预测年收入是否大于50K美元 个人简介 🏘️🏘️个人主页:以山河作礼。 🎖️🎖️:Python领域新星创作者,CSDN实力新星认证,C
Leetcode 3701 · Find Nearest Right Node in Binary Tree (遍历和BFS好题)
3701 · Find Nearest Right Node in Binary TreePRE Algorithms This topic is a pre-release topic. If you encounter any problems, please contact us via “Problem Correction”, and we will upgrade your acco
K近邻算法(K-Nearest Neighbors,KNN)
K近邻算法(K-Nearest Neighbors,KNN)是一种基本的监督学习算法,常用于分类和回归任务。KNN的基本思想是通过测量不同样本点之间的距离,将新样本的类别标签赋予其K个最近邻居中出现最频繁的类别。 以下是KNN的基本原理和使用方法: 基本原理 距离度量: KNN通常使用欧氏距离(Euclidean distance)或其他距离度量来衡量样本点之间的相似性。邻居选择: 对于
我的cs231n学习笔记(2)lecture2-K Nearest Neighbor
lecture2:KNN 根据KNN算法所做的表现效果并不是很好: 我们可以通过将k值调大的方法使算法表现的更好,但还有另外一个选择,更换距离函数。L2 distance距离函数也叫做欧式距离函数(Euclidean distance) 不同的距离度量函数在预测的空间里对底层的几何或拓扑结构做出不同的假设。 kNN模拟 k值、距离函数成为超参数(hyperparameters),因为他们并
《统计学习方法》第三章:k-近邻算法(K-Nearest Neighbors)
监督学习,多分类、回归 计算输入点与数据集点距离,升序排序,选取数据集里前k个点,计算这k个点对应类别(也就是label)出现的概率,最大概率的分类就是输入点的分类。 目录 一、分类问题 二、监督学习 三、KNN算法原理和流程 1、工作原理 2、一般流程 3、距离计算 4、k值的选择 1)如果选择较小的K值 2)如果选择较大的K值 三、Python代码 1、数据导入
K-Nearest-Neighbours 和 kd 树
什么是KNN? KNN算法是没有学习过程的。它将所有已知数据存储起来,当要预测某一新数据时,使用某种距离度量选择离该新数据在特种空间中最近的K个点,根据分类决策规则,一般是多数投票规则对新数据进行分类。 怎样构造KNN: 1) 距离度量 LP距离。在P=1时是曼哈顿距离,P=2时是欧式距离,P为无穷大时是切比雪夫距离。也可以自己定义距离。 2)K值选择 K只选择太小,容易过拟合