本文主要是介绍【机器学习】k近邻(k-nearest neighbor )算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 0. 前言
- 1. 算法原理
- 1.1 距离度量
- 1.2 参数k的选择
- 2. 优缺点及适用场景
- 3. 改进和扩展
- 4. 案例
- 5. 总结
0. 前言
k近邻(k-nearest neighbors,KNN)算法是一种基本的监督学习算法,用于分类和回归问题。k值的选择、距离度量及分类决策规则是k近邻法的三个基本要素。
1. 算法原理
给定一个训练数据集,KNN算法通过计算待分类样本与训练数据集中各个样本的距离,选取距离最近的k个样本,然后根据这k个样本的类别进行投票(分类问题)或者求平均值(回归问题),以确定待分类样本的类别或者值。
注:分类问题中常使用多数表决作为决策规则,回归问题中常使用平均或加权平均作为决策规则
1.1 距离度量
距离度量在机器学习和数据挖掘领域中是一项基础且至关重要的工作。它用于衡量数据集中样本之间的相似性或差异性。在KNN算法中,距离度量被用来衡量待分类样本与训练数据集中各个样本之间的距离,以便确定最近的邻居。KNN算法常用的距离度量方法包括欧氏距离和曼哈顿距离。
- 欧氏距离(Euclidean Distance)
欧氏距离是最常见的距离度量方法之一,也是我们通常所理解的“直线距离”。对于两个样本向量 p = ( p 1 , p 2 , . . . , p n ) \mathbf{p}=(p_1, p_2, ...,p_n) p=(p1,p2,...,pn)和 q = ( q 1 , q 2 , . . . , q n ) \mathbf{q}=(q_1, q_2, ...,q_n) q=(q1,q2,...,qn),它们之间的欧氏距离可以表示为:
d ( p , q ) = ∑ i = 1 n ( p i − q i ) 2 d(\mathbf{p}, \mathbf{q}) = \sqrt{\sum_{i=1}^{n}(p_i - q_i)^2} d(p,q)=i=1∑n(pi−qi)2 - 曼哈顿距离(Manhattan Distance)
曼哈顿距离又称为城市街区距离,它是两个点在标准坐标系上的绝对轴距总和。两个样本向量之间的曼哈顿距离可以表示为: d ( p , q ) = ∑ i = 1 n ∣ p i − q i ∣ d(\mathbf{p}, \mathbf{q}) = \sum_{i=1}^{n}|p_i - q_i| d(p,q)=i=1∑n∣pi−qi∣
1.2 参数k的选择
选择适当的 k 值对 K 近邻算法的性能至关重要。选择 k 值时,需要权衡模型的复杂度和泛化能力,通常通过交叉验证等方法来确定。
下面是一些常见的选择 k 值的方法:
- 经验法:选择一个较小的 k 值,例如 3 或 5。这种方法适用于较小的数据集和较简单的问题
- 奇数选择:为了避免平局情况的发生,通常选择奇数的 k 值,这样在进行投票时可以避免平票的情况
- 交叉验证:通过交叉验证来选择最优的 k 值。可以采用 k 折交叉验证,将训练数据集划分为 k 个子集,每次将其中一个子集作为验证集,其余子集作为训练集,重复 k 次计算模型的性能指标(如准确率、F1 分数等),然后选取性能最好的 k 值
- 网格搜索:结合交叉验证,使用网格搜索方法在指定范围内搜索最优的 k 值。通过在给定的 k 值范围内进行搜索,并评估每个 k 值的性能,最终选择性能最好的 k 值。
- 调整邻域大小:对于特定问题,可能需要调整邻域的大小,即样本点在特征空间中的密度。可以通过逐步增加或减少 k 值来探索模型的性能变化。
在实践中,选择 k 值时需要考虑数据集的大小、类别分布、特征的数量和类型等因素。较大的 k 值会使模型更加平滑,减少噪声的影响,但可能导致模型欠拟合;而较小的 k 值可能会使模型更加复杂,容易受到局部极值点的影响,但也更容易受到噪声的干扰。因此,选择合适的 k 值需要在模型的泛化能力和准确性之间进行权衡。
2. 优缺点及适用场景
优点:
- 实现简单,易于理解
- 适用于多分类和回归问题
- 对于特征维度较高的数据也能够有效地进行分类
缺点:
- 需要保存全部的训练数据,当训练数据集较大时,内存消耗较大
- 对于每个待分类样本,都需要计算与所有训练样本的距离,当训练数据集较大时,计算复杂度较高
- 对于样本不平衡的数据,可能会导致预测偏倚
适用场景:
- 适用于样本数量较少、类别较少、特征维度较低的情况
- 可以用于初步了解数据分布、进行数据探索性分析等
3. 改进和扩展
- 加权KNN:通过给距离较近的样本赋予更高的权重,改善模型性能。
- KD树、球树等数据结构:用于加速KNN算法的搜索过程,降低计算复杂度。
- 距离加权KNN、半径最近邻等改进算法。
4. 案例
以《动手学机器学习》中高斯数据集的分类为例(官方项目地址),高斯数据集包含一些平面上的点,分别由两个独立的二维高斯分布随机生成。
首先,导入数据集并分析数据结构
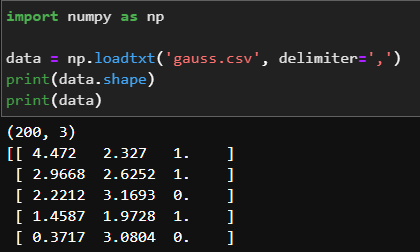
可以看到,数据一共有200个样本,每个样本包含x,y坐标和对应的类别。然后对数据进行可视化:
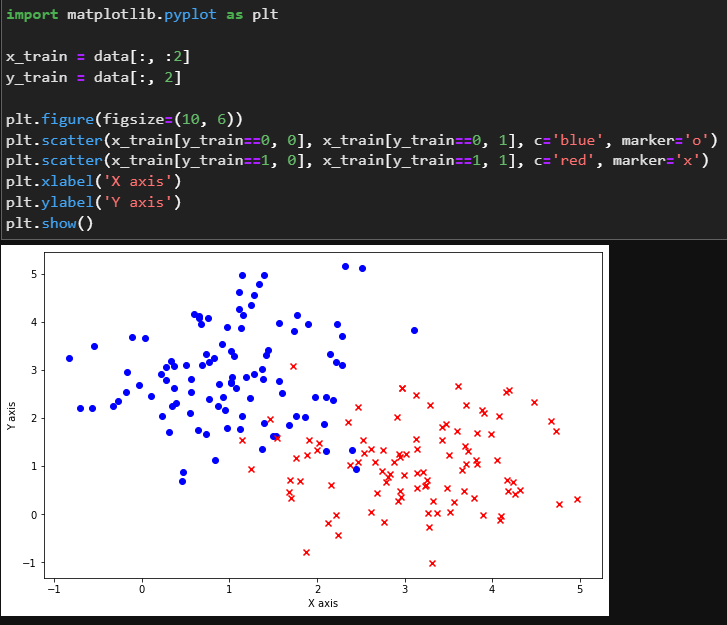
将整个数据集作为训练集,将平面上其他点作为测试集。由于平面上的点是连续的,因此采用均匀网格采样获取离散点作为测试样本:
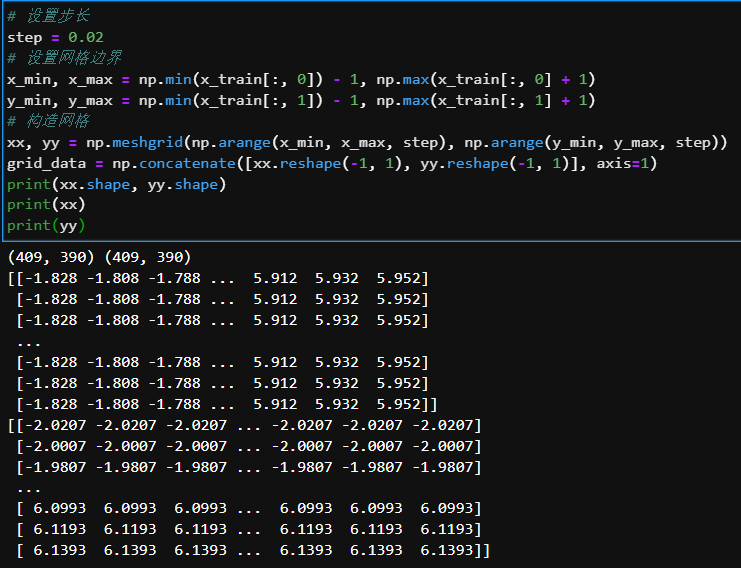
通过np.meshgrid函数生成了409*390个网格点,xx和yy分别为横坐标和纵坐标,将两者reshape和拼接后得到的grid_data作为测试集。使用sklearn中的KNN对测试集进行分类:

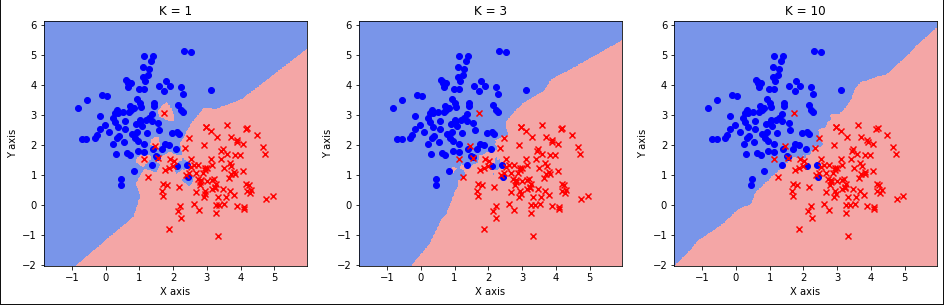
从分类结果中可以看到,随着K的增大,分类边界逐渐平滑,但同时错分概率也逐渐变大。
5. 总结
总的来说,KNN算法是一种简单而有效的分类和回归方法,尤其适用于小型数据集和低维特征空间。然而,在大规模数据集和高维特征空间下,KNN算法的计算复杂度和内存消耗可能会成为问题,因此在实际应用中需要谨慎选择。
TODO
- kd树提高k近邻算法效率的原理
这篇关于【机器学习】k近邻(k-nearest neighbor )算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







