本文主要是介绍《统计学习方法》第三章:k-近邻算法(K-Nearest Neighbors),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
监督学习,多分类、回归
计算输入点与数据集点距离,升序排序,选取数据集里前k个点,计算这k个点对应类别(也就是label)出现的概率,最大概率的分类就是输入点的分类。
目录
一、分类问题
二、监督学习
三、KNN算法原理和流程
1、工作原理
2、一般流程
3、距离计算
4、k值的选择
1)如果选择较小的K值
2)如果选择较大的K值
三、Python代码
1、数据导入
2、算法和关键函数
1)分类算法流程和关键函数
2)文本中解析数据
3)用matplotlib绘制散点图
4)数据归一化
5)使用k-近邻算法的手写识别系统
6)测试算法
3、分类算法
1)分类算法流程
2)kNN中分类算法
四、kNN算法改进
1、KNN面临的挑战
2、算法改进
1)距离度量
2)KD树
一、分类问题

二、监督学习


三、KNN算法原理和流程


1、工作原理
-
存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每个数据与所属分类的对应关系。
-
输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。
-
一般来说,只选择样本数据集中前N个最相似的数据。分类数K一般不大于20,最后,选择k个中出现次数最多的分类,作为新数据的分类。
2、一般流程
-
收集数据:可以使用任何方法
-
准备数据:距离计算所需要的数值,最后是结构化的数据格式。
-
分析数据:可以使用任何方法
-
训练算法:(此步骤kNN)中不适用
-
测试算法:计算错误率
-
使用算法:首先需要输入样本数据和结构化的输出结果,然后运行k-近邻算法判定输入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理。
3、距离计算
![]()
![]()
![]()
![]()
![]()
 p=1对应最里面的棱形;p=2对应中间的圆;p=∞对应外面的矩形
p=1对应最里面的棱形;p=2对应中间的圆;p=∞对应外面的矩形
4、k值的选择
1)如果选择较小的K值
- “学习”的近似误差(approximation error)会减小,但 “学习”的估计误差(estimation error) 会增大
- 噪声敏感
- K值的减小就意味着整体模型变得复杂,容易发生过拟合
2)如果选择较大的K值
- 减少学习的估计误差,但缺点是学习的近似误差会增大
- K值的增大,就意味着整体的模型变得简单
三、Python代码
1、数据导入
from numpy import *
import operator
def createDataSet():group=array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])labels=['A','A','B','B']return group,lablesgroup,labels=kNN.createDataSet()Python 数组和numpy矩阵的关系:
>>> a=[[1,2,3,4],[5,6,7,8],[9,10,11,12]]
>>> c=zeros((3,4))
>>> c
array([[ 0., 0., 0., 0.],[ 0., 0., 0., 0.],[ 0., 0., 0., 0.]])
>>> c[0,:]=a[0]
>>> c
array([[ 1., 2., 3., 4.],[ 0., 0., 0., 0.],[ 0., 0., 0., 0.]])2、算法和关键函数
1)分类算法流程和关键函数
- Shape
group,labels=kNN.createDataSet()
group.shape
group.shape[0]# shape用法
import numpy as np
x = np.array([[1,2,5],[2,3,5],[3,4,5],[2,3,6]])
#输出数组的行和列数
print x.shape #结果: (4, 3)
#只输出行数
print x.shape[0] #结果: 4
#只输出列数
print x.shape[1] #结果: 3- Tile
tile([1.0,1.2],(4,1))
# 输出
array([[ 1. , 1.2],[ 1. , 1.2],[ 1. , 1.2],[ 1. , 1.2]])
tile([1.0,1.2],(4,1))-group
#输出
array([[ 0. , 0.1],[ 0. , 0.2],[ 1. , 1.2],[ 1. , 1.1]])
a=(tile([1.0,1.2],(4,1))-group)**2
#输出
array([[ 0. , 0.01],[ 0. , 0.04],[ 1. , 1.44],[ 1. , 1.21]])- Argsort
b=a.sum(axis=1)
c=b**0.5
d=c.argsort()
>>> d
array([0, 1, 3, 2])- 字典的使用
classCount={} #字典for i in range(k): #列表的扩展voteIlabel = labels[sortedDistIndicies[i]]classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)return sortedClassCount[0][0]kNN.classify0([0,0.2],group,labels,3)
>>'B'2)文本中解析数据
- 文件读取相关函数:Open()、Readlines、Zeros()
3)用matplotlib绘制散点图
import matplotlib
>>> import matplotlib.pyplot as plt>>> fig=plt.figure()
>>> ax=fig.add_subplot(111)
>>> ax.scatter(datingDataMat[:,1],datingDataMat[:,2])
<matplotlib.collections.PathCollection object at 0x01D8F590>
>>> plt.show()>>> fig=plt.figure()
>>> ax=fig.add_subplot(111)
>>>ax.scatter(datingDataMat[:,1],datingDataMat[:,2],15.0*array(datingLabels),15.0*array(datingLabels))
>>> plt.show()4)数据归一化
def autoNorm(dataSet):minVals = dataSet.min(0)maxVals = dataSet.max(0)ranges = maxVals - minValsnormDataSet = zeros(shape(dataSet))m = dataSet.shape[0]normDataSet = dataSet - tile(minVals, (m,1))normDataSet = normDataSet/tile(ranges, (m,1)) #element wise dividereturn normDataSet, ranges, minVals>>> n,r,m=kNN.autoNorm(datingDataMat)
>>> n
array([[ 0.44832535, 0.39805139, 0.56233353],[ 0.15873259, 0.34195467, 0.98724416],[ 0.28542943, 0.06892523, 0.47449629],..., [ 0.29115949, 0.50910294, 0.51079493],[ 0.52711097, 0.43665451, 0.4290048 ],[ 0.47940793, 0.3768091 , 0.78571804]])
>>> r
array([ 9.12730000e+04, 2.09193490e+01, 1.69436100e+00])
>>> m
array([ 0. , 0. , 0.001156])5)使用k-近邻算法的手写识别系统
# 准备数据,将图像转换为测试向量 32x32
def img2vector(filename):returnVect = zeros((1,1024))fr = open(filename)for i in range(32):lineStr = fr.readline()for j in range(32):returnVect[0,32*i+j] = int(lineStr[j])return returnVect
6)测试算法
def datingClassTest():hoRatio = 0.50 #hold out 10%datingDataMat,datingLabels = file2matrix('datingTestSet2.txt') #load data setfrom filenormMat, ranges, minVals = autoNorm(datingDataMat)m = normMat.shape[0]numTestVecs = int(m*hoRatio)errorCount = 0.0for i in range(numTestVecs):classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])if (classifierResult != datingLabels[i]): errorCount += 1.0print "the total error rate is: %f" % (errorCount/float(numTestVecs))print errorCount>>> testVector=kNN.img2vector('testDigits/0_13.txt')
>>> tesVector[0,0:31]3、分类算法
1)分类算法流程
对未知类别的数据集中的每个点依次执行以下操作:
- 计算已知类别数据集众多点与当前点之间的距离
- 按照距离递增次序排序
- 选取与当前点距离最小的k个点
- 群定前k个点所在类别的出现频率
2)kNN中分类算法
def classify0(inX, dataSet, labels, k):dataSetSize = dataSet.shape[0]diffMat = tile(inX, (dataSetSize,1)) - dataSetsqDiffMat = diffMat**2sqDistances = sqDiffMat.sum(axis=1)distances = sqDistances**0.5sortedDistIndicies = distances.argsort() classCount={} for item in range(k):voteIlabel = labels[sortedDistIndicies[item]]classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)return sortedClassCount[0][0]四、kNN算法改进
1、KNN面临的挑战

2、算法改进
1)距离度量
马氏距离(Mahalanobis Distance):



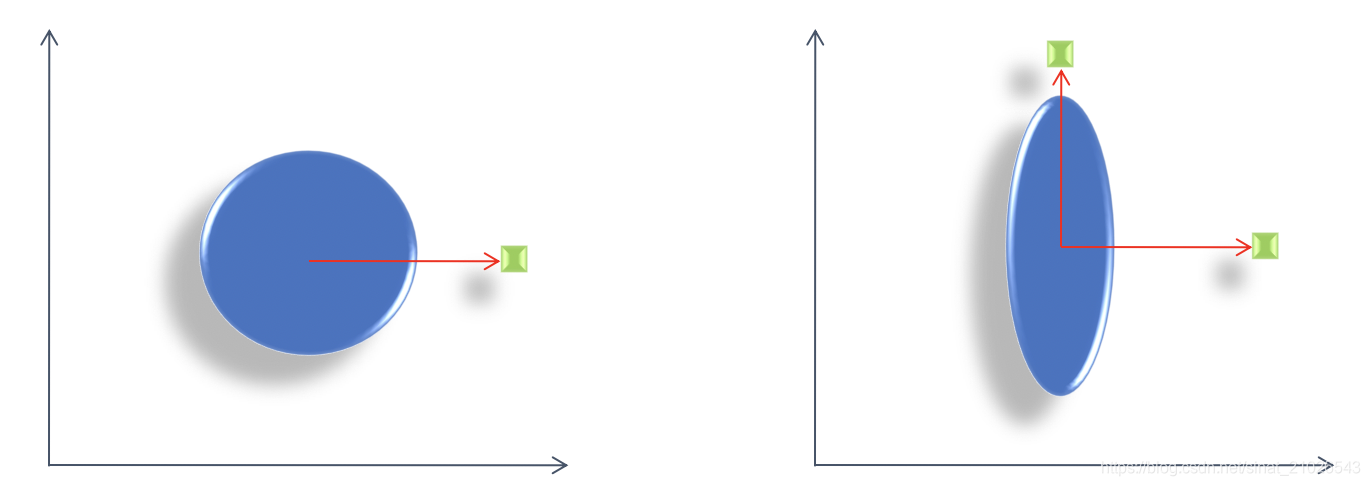
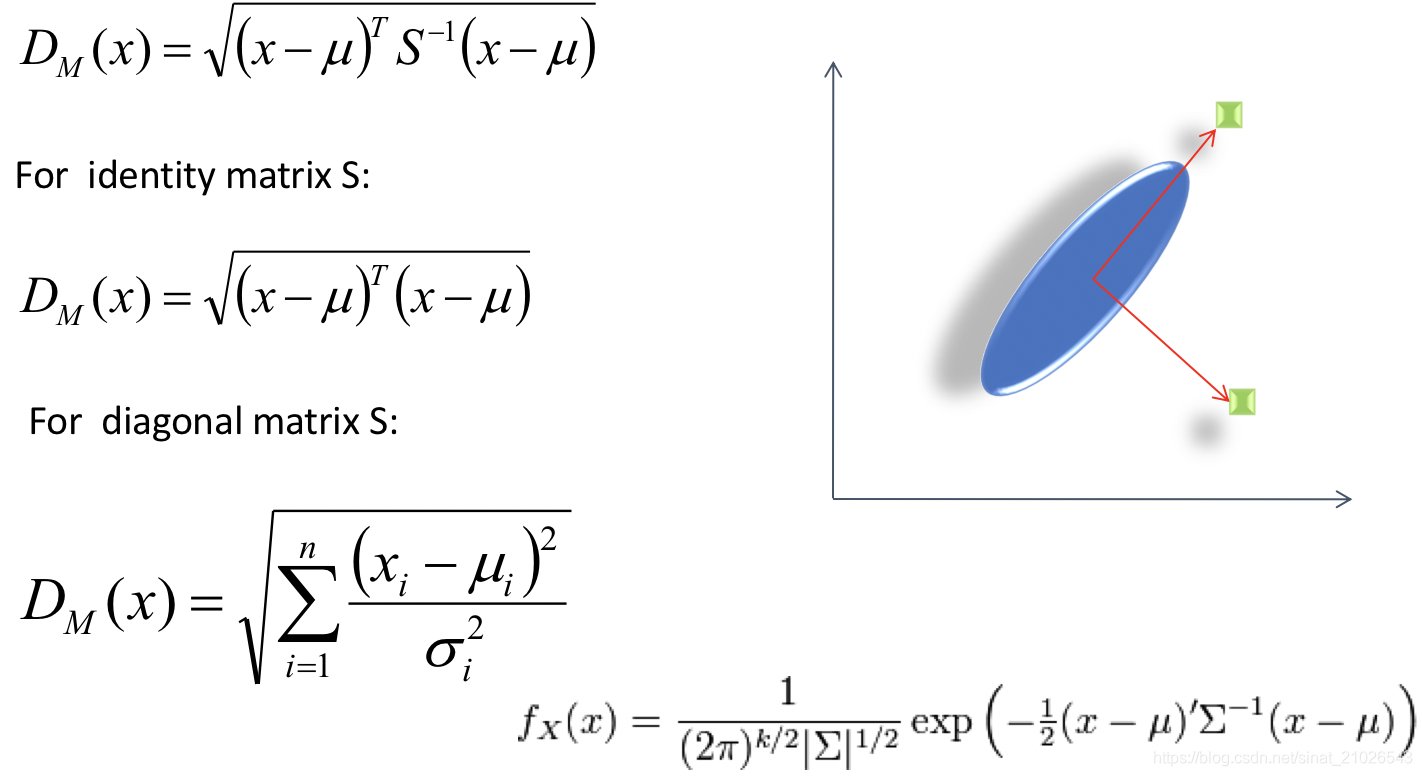
马氏距离NUMPY示例:
import numpy
x = numpy.array([[3,4],[5,6],[2,2],[8,4]])
xT = x.T
D = numpy.cov(xT)
invD = numpy.linalg.inv(D)
tp = x[0] – x[1]
print numpy.sqrt(dot(dot(tp, invD), tp.T)) Ø 由 P.C. Mahalanobis提出Ø 基于 样本分布 的一种距离测量Ø 考虑到各种 特性之间的联系 (例如身高和体重),可以 消除样本间的相关性Ø 广泛用于 分类 和 聚类分析

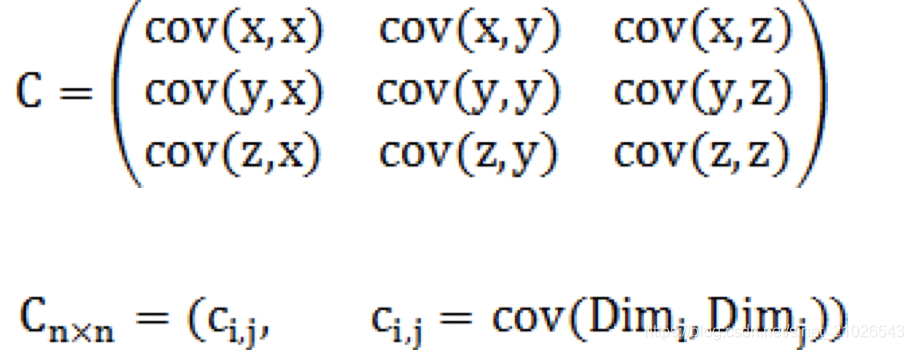

2)KD树
- KD树是一种对 K 维空间中的实例点进行存储以便对其进行 快速检索 的树形数据结构。
- KD树是 二叉树 ,表示对K 维空间的一个划分( partition), 构造KD 树相当于不断地用垂直于坐标轴的超平面将 k 维空间切分,构成一系列的 k 维超矩形区域, KD 树的每个结点对应于一个 k 维超矩形区域。



这篇关于《统计学习方法》第三章:k-近邻算法(K-Nearest Neighbors)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




