本文主要是介绍K-Nearest-Neighbours 和 kd 树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
什么是KNN?
KNN算法是没有学习过程的。它将所有已知数据存储起来,当要预测某一新数据时,使用某种距离度量选择离该新数据在特种空间中最近的K个点,根据分类决策规则,一般是多数投票规则对新数据进行分类。
怎样构造KNN:
1) 距离度量
LP距离。在P=1时是曼哈顿距离,P=2时是欧式距离,P为无穷大时是切比雪夫距离。也可以自己定义距离。
2)K值选择
K只选择太小,容易过拟合。K选择过大,近似误差变大。
常用的方法是从k=1开始,使用检验集估计分类器的误差率。重复该过程,每次K增值1,允许增加一个近邻。选取产生最小误差率的K。
一般k的取值不超过20,上限是n的开方,随着数据集的增大,K的值也要增大。
3)样本特征做归一化处理??(why?)
如果一个特征值域范围非常大,那么距离计算就主要取决于这个特征,从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要)。归一化可以提高预测精度。
归一化的方法
最值归一化:将所有数据映射到同一尺度;这种方式受异常值影响比较大;适用于有明显边界的情况;
x = x-xmin /xmax - xmin
均值方差归一化:另处理好的数据正态分布
怎么对测试集进行归一化:
使用训练集归一化的scaler对测试集进行处理
两种的区别不清楚
4)所有特征要做可比较的量化(why?,不明白)
若是样本特征中存在非数值的类型,必须采取手段将其量化为数值。例如样本特征中包含颜色,可通过将颜色转换为灰度值来实现距离计算。
优点和缺点:
KNN算法是最简单有效的分类算法,简单且容易实现。当训练数据集很大时,需要大量的存储空间,而且需要计算待测样本和训练数据集中所有样本的距离,所以非常耗时。
KNN对于随机分布的数据集分类效果较差,对于类内间距小,类间间距大的数据集分类效果好,而且对于边界不规则的数据效果好于线性分类器。
KNN对于样本不均衡的数据效果不好,需要进行改进。改进的方法时对k个近邻数据赋予权重,比如距离测试样本越近,权重越大。(不懂,是加权?)
KNN很耗时,时间复杂度为O(n),一般适用于样本数较少的数据集,当数据量大时,可以将数据以树的形式呈现,能提高速度,常用的有kd-tree和ball-tree。
多分类问题中,KNN比SVM要好。(看了SVM再来说明为什么)
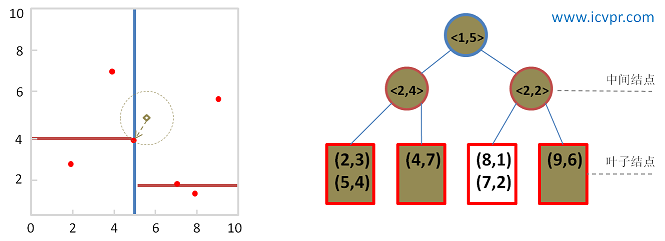
KD-TREE
KD-TREE
这篇关于K-Nearest-Neighbours 和 kd 树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!