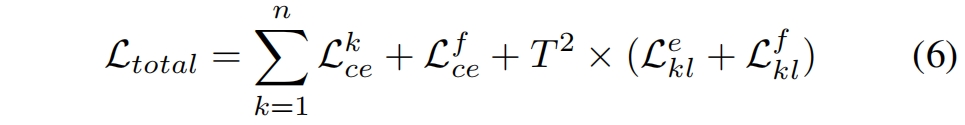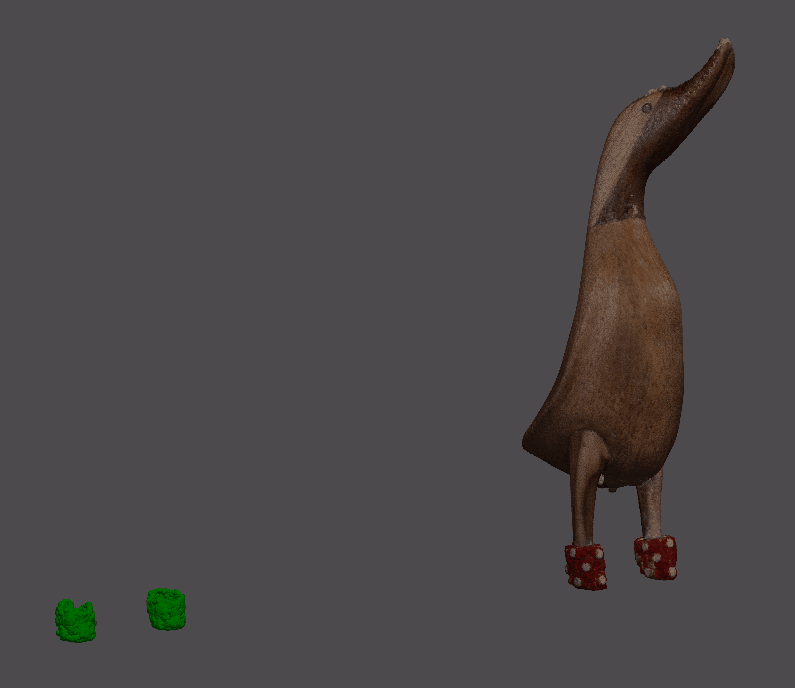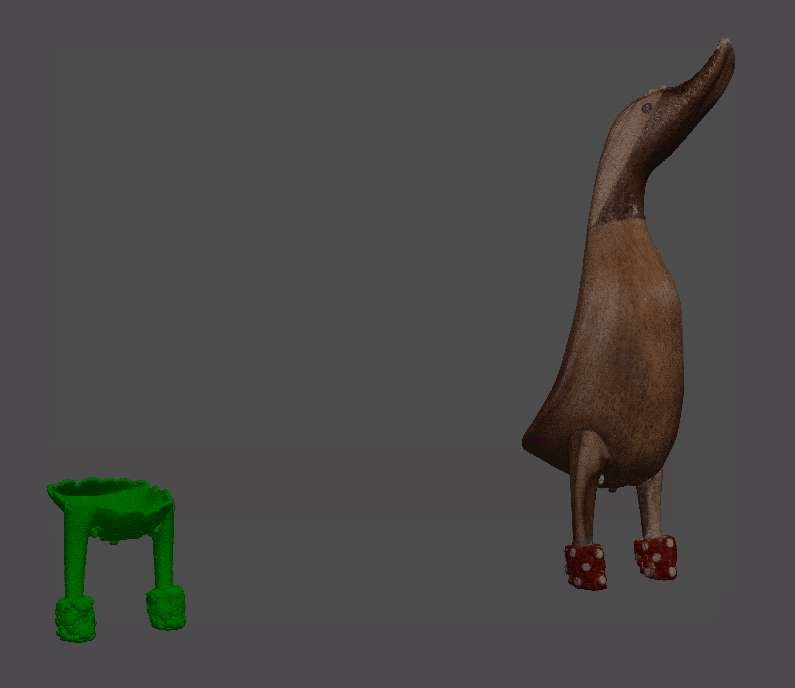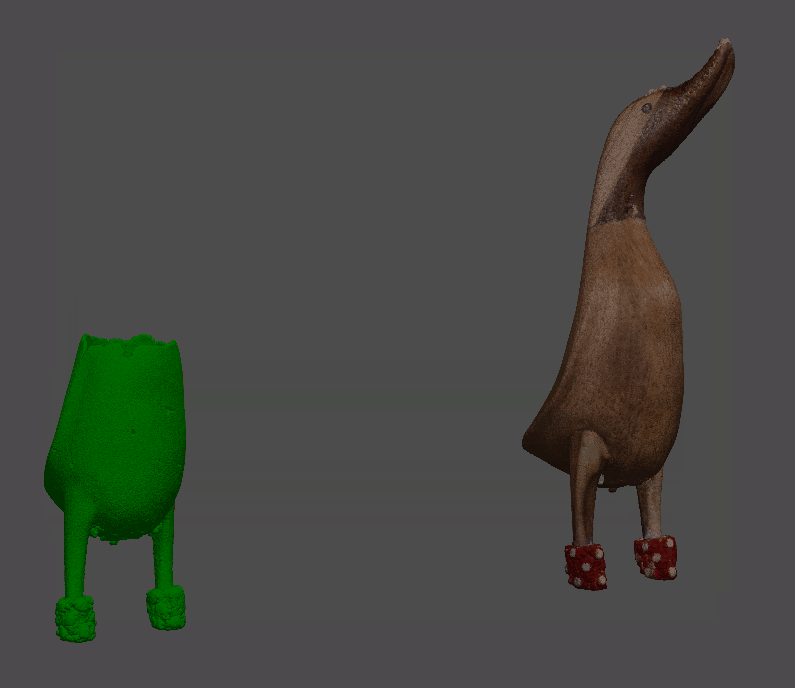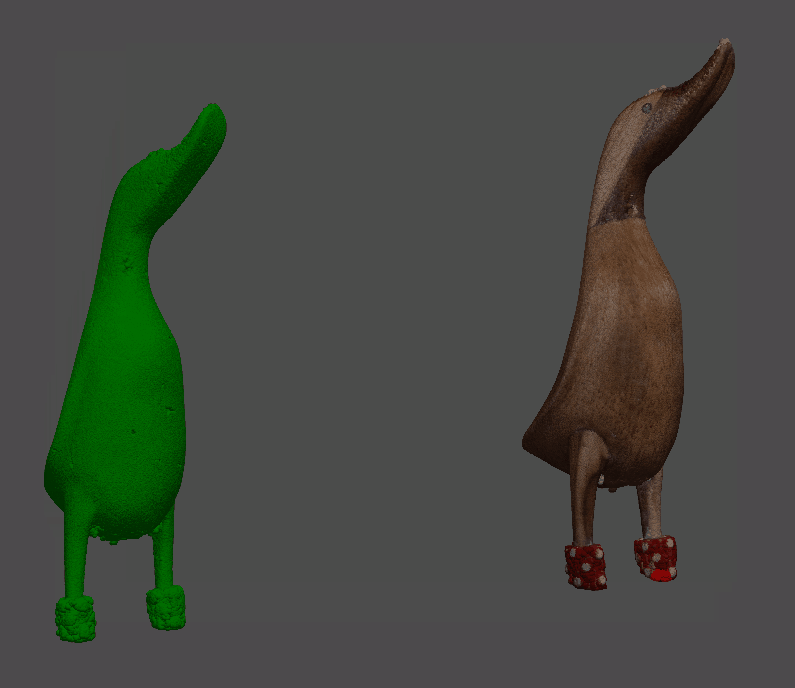kd专题
kd-tree理论以及在PCL 中的代码的实现
(小技巧记录:博客园编辑的网页界面变小了使用Ctrl ++来变大网页字体) 通过雷达,激光扫描,立体摄像机等三维测量设备获取的点云数据,具有数据量大,分布不均匀等特点,作为三维领域中一个重要的数据来源,点云主要是表征目标表面的海量点的集合,并不具备传统网格数据的几何拓扑信息,所以点云数据处理中最为核心的问题就是建立离散点间的拓扑关系,实现基于邻域关系的快速查找。 k-d树 (k-dime
KD-Tree 的一些理解--
阅读文档:Wikipedia 上的 KD Tree 。 https://en.wikipedia.org/wiki/K-d_tree 引言 In computer science, a k-d tree (short for k-dimensional tree) is a space-partitioning data structure for organizing points in a
【C++PCL】点云处理Kd-tree原理
作者:迅卓科技 简介:本人从事过多项点云项目,并且负责的项目均已得到好评! 公众号:迅卓科技,一个可以让您可以学习点云的好地方 重点:每个模块都有参数如何调试的讲解,即调试某个参数对结果的影响是什么,大家有问题可以评论哈,如果文章有错误的地方,欢迎来指出错误的地方。 目录 1.原理介绍 1.原理介绍 kd-tree是散乱点云的一种储存结构,它是一种
KD-TREE 算法原理
KD-TREE 算法原理 http://www.oneie.com/index.php/qyjs/47-txcl/1532-kd-tree 本文介绍一种用于高维空间中的快速最近邻和近似最近邻查找技术——Kd- Tree(Kd树)。Kd-Tree,即K-dimensional tree,是一种高维索引树形数据结构,常用于在大规模的高维数据空间进行最近邻查找(Nearest Neighbor
机器学习--从K近邻算法、距离度量谈到KD树、SIFT+BBF算法
引言 最近在面试中,除了基础 & 算法 & 项目之外,经常被问到或被要求介绍和描述下自己所知道的几种分类或聚类算法(当然,这完全不代表你将来的面试中会遇到此类问题,只是因为我的简历上写了句:熟悉常见的聚类 & 分类算法而已),而我向来恨对一个东西只知其皮毛而不得深入,故写一个有关数据挖掘十大算法的系列文章以作为自己备试之用,甚至以备将来常常回顾思考。行文杂乱,但侥幸若能对读者起到一
KD-Trees(K-dimensional树)和Octrees(八叉树
KD-Trees(K-dimensional树)和Octrees(八叉树)是两种常用的数据结构,它们在多维空间中用于高效地存储和查询数据。这两种结构在计算机科学中有着广泛的应用,尤其是在图形学、机器人学、空间索引和最近邻搜索等领域。 KD-Trees KD-Trees是一种二叉树结构,用于组织K维空间中的点。在KD-Trees中,每个节点代表一个K维空间中的点,并且树是通过递归地将空间分割成两
K近邻算法基础:KD树的操作
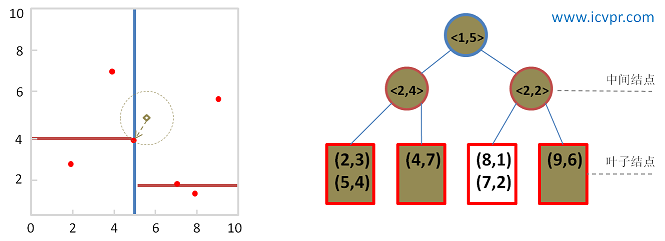
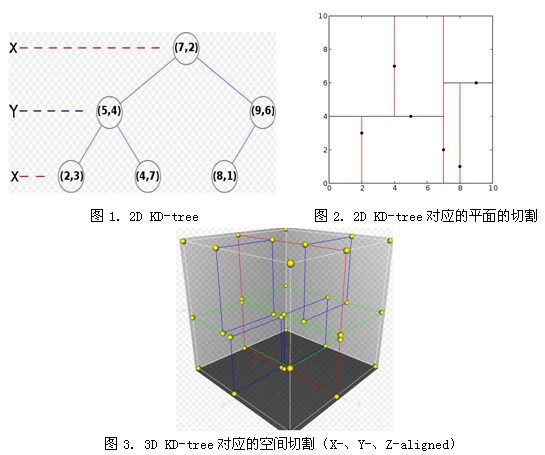
Kd-树概念 Kd-树 其实是K-dimension tree的缩写,是对数据点在k维空间中划分的一种数据结构。其实,Kd-树是一种平衡二叉树。 举一示例: 假设有六个二维数据点 = {(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},数据点位于二维空间中。为了能有效的找到最近邻,Kd-树采用分而治之的思想,即将整个空间划分为几个小部分。六个二维数据点生成的Kd-树的
3D,kd-tree算法原理
作为三维领域中一个重要的数据来源,点云主要是表征目标表面的海量点的集合,并不具备传统网格数据的几何拓扑信息,所以点云数据处理中最为核心的问题就是建立离散点间的拓扑关系,实现基于邻域关系的快速查找。 几何拓扑是计算几何学中的一个重要概念,指的是描述几何形状的空间结构和连接关系的数学模型。在几何拓扑中,主要考虑的是几何对象的形状、边界、顶点以及它们之间的关系,而不涉及具体的度量或尺寸。 几何拓扑可
KD_Tree 【bzoj2648 bzoj2716】SJY摆棋子 [voilet 3] 天使玩偶
题目大意: 维护一堆点,支持插入一个点和查询距离一个给定的点的曼哈顿距离最近的点。 题目分析:(KD_Tree) 据说还可以用CDQ分治做,但是因为要分四个象限讨论,很麻烦的说呀QAQ 我这种萌萌哒蒟蒻自然去学KDT啦~(>▽<)~ KD_Tree 主要应用于解决多维空间内一堆点的问题。 这道题只要正常建树并且插入就可以了。 查询的时候相当于爆搜+剪枝,每搜到一个点都写给两个儿子写一
【HDU】2021杭电暑假集训营(第一场):KD-Graph 思维 + 并查集
传送门 题意 n个顶点,给出m条边的信息。现在问是否存在一个最小的D值恰好使原图变为k个连通的部分。 若顶点p和q (p≠q)连通,则p和q之间最长边小于或等于D(不是总路径长度)。 若点p和q (p≠q)不连通,则p和q之间最长边不可能小于或者等于D。 分析 我们把所有点看成 n n n个连通块,然后去动态合并 把所有边按照边权排序,如果两个端点不在同一个连通块内,就进行合并,一直合并
使用KD树进行最近邻查找的例子
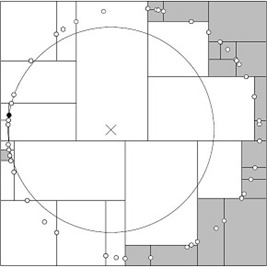
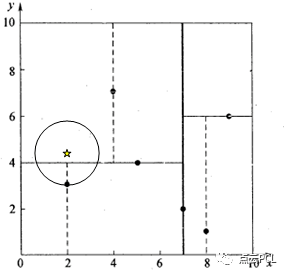
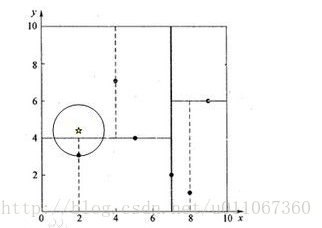
使用KD树进行最近邻查找的例子 例1: 查询点(2.1,3.1) 星号表示要查询的点(2.1,3.1)。通过二叉搜索,顺着搜索路径很快就能找到最邻近的近似点,也就是叶子节点(2,3)。而找到的叶子节点并不一定就是最邻近的,最邻近肯定距离查询点更近,应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻,还需要进行相关的‘回溯'操作。 也就是说,算法首先沿搜索路径反向查找是否
14 Games101 - 笔记 - 光线追踪(利用包围盒技术加速光线追踪(KD-Tree and BVH)
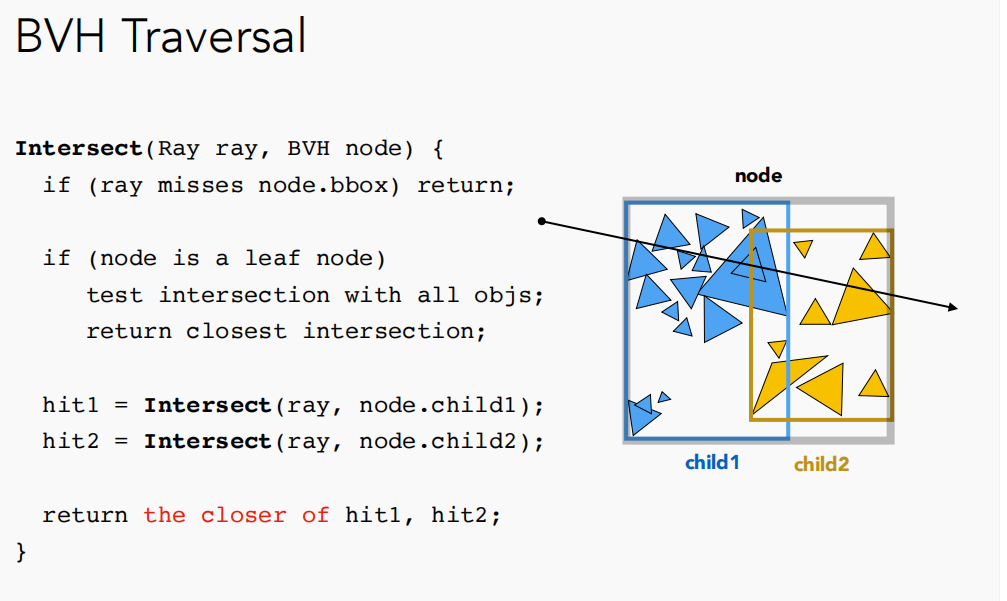
14 光线追踪(利用包围盒技术加速光线追踪(KD-Tree and BVH) 在上一节中,我们介绍了whited-style光线追踪的原理,以及实现细节。相比与光栅化中所使用的的Blinn-Phong模型,光线追踪显著了提升了图像质量,但随之而来的问题是渲染速度过慢。因为在判断光线与场景交点的时候,需要去进行所有三角形面与光线的求交,而且这仅仅是对一个像素而言。 那么总体来说光是进行光线与三角形
ElasticSearch学习篇10_Lucene数据存储之BKD动态磁盘树(论文Bkd-Tree: A Dynamic Scalable kd-Tree)
前言 基础的数据结构如二叉树衍生的的平衡二叉搜索树通过左旋右旋调整树的平衡维护数据,靠着二分算法能满足一维度数据的logN时间复杂度的近似搜索。对于大规模多维度数据近似搜索,Lucene采用一种BKD结构,该结构能很好的空间利用率和性能。 本片博客主要学习常见的多维数据搜索数据结构、KD-Tree的构建、搜索过程以针对高维度数据容灾的优化的BBF算法,通过读论文学习BKD结构原理,总结对数算法
金融知识分享系列之:KD指标
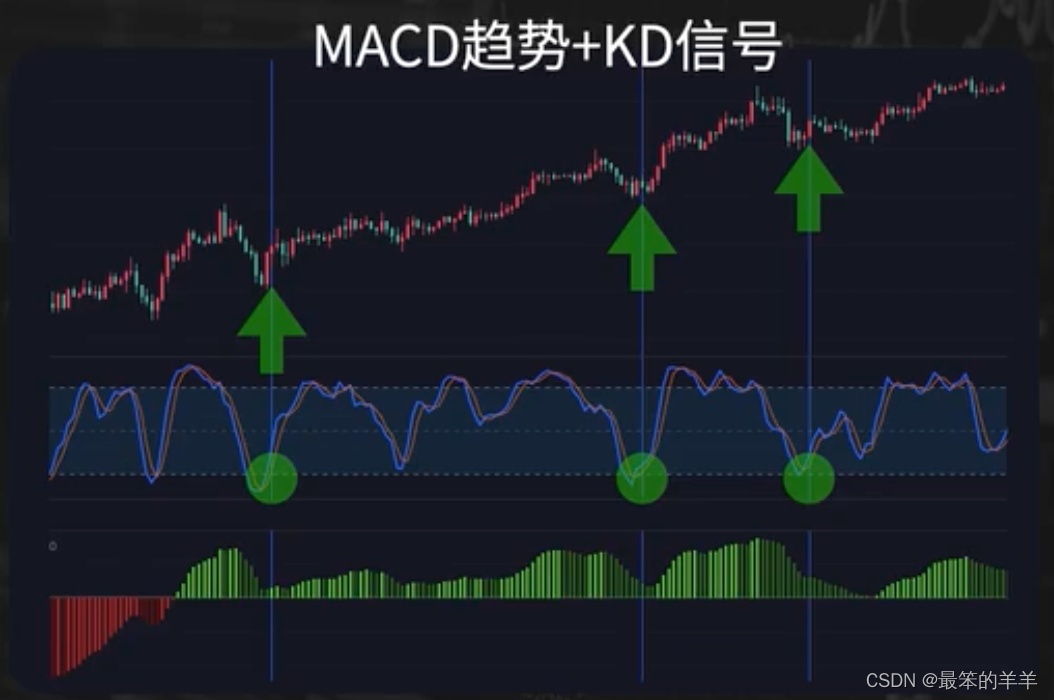
金融知识分享系列之:KD指标 一、KD指标二、KD指标计算三、KD指标原理四、KD指标应用 一、KD指标 KD信号提供入场的工具 名称:随机震荡指标参数:(9,3,3)组成:K线,D线,20轴,80轴 二、KD指标计算 简单来说,D值就是K值周期为3的加权移动平均线KD指标的默认参数(9,3,3)9对应的就是KD指标的取值范围第一个3对应的就是K值,也就是RSV的加
1721: on xh kd lh(破译凯撒密码)
恺撒密码 1721: on xh kd lh Time Limit: 1 Sec Memory Limit: 128 MB Submit: 113 Solved: 103 [Submit][Status][Web Board] Description fnmf wh mh on xh kd lh vdm ygd cn sh lt rgh ygd xmf cd fdh mh xh fd rgt m
knn算法与kd树实现
最近邻法和k-近邻法 下面图片中只有三种豆,有三个豆是未知的种类,如何判定他们的种类? 提供一种思路,即:未知的豆离哪种豆最近就认为未知豆和该豆是同一种类。由此,我们引出最近邻算法的定义:为了判定未知样本的类别,以全部训练样本作为代表点,计算未知样本与所有训练样本的距离,并以最近邻者的类别作为决策未知样本类别的唯一依据。但是,最近邻算法明显是存在缺陷的,比如下面的例子:有一个未知形
【计算几何4】正交区域查询和KD-Tree概念
目录 一、说明 二、正交区域查找 2.1 定义 2.2 引进KD树 2.3 构造Kd树 2.4 二维的例子说明原理 三、三维度示例研究 3.1 假如下面例子 3.2 构建示例代码(python) 一、说明 kd 树是一种二叉树数据结构,可以用来进行高效的 kNN 计算。kd 树算法偏于复杂,本篇将先介绍以二叉树的形式来记录和索引空间
变分互信息蒸馏(Variational mutual information KD)
原文标题是Variational Information Distillation for Knowledge Transfer,是CVPR2019的录用paper。 VID方法 思路比较简单,就是利用互信息(mutual information,MI)的角度,增加teacher网络与student网络中间层特征的MI,motivation是因为MI可以表示两个变量的依赖程度,MI越大,表明
Feature Fusion for Online Mutual KD
paper:Feature Fusion for Online Mutual Knowledge Distillation official implementation:https://github.com/Jangho-Kim/FFL-pytorch 本文的创新点 本文提出了一个名为特征融合学习(Feature Fusion Learning, FFL)的框架,该框架通过一个组合并行网
KD随机振荡指标简介
KD随机振荡指标简介 Stochastics指标又名KDJ 指标 ,是由 George Lane 首创的,最早用于期货市场。Stochastics指标在图表上采用%K和%D两条线,在设计中综合了动量 观念、强弱指标与移动平均线的优点,在计算过程中主要研究高低价位与收市价的关系,反映价格走势的强弱和超买超卖现象。它的主要理论依据是:当价格上涨时,收市价倾向于接近当日价格区间的上端;相反,在下降
计算机视觉 基于Open3D了解用于网格和点云邻域分析的KD树和八叉树
一、简述 距离计算和邻域分析是理解网格和点云的形状、结构和特征的重要工具。我们这里要基于一些3D库来提取基于距离的信息并将其可视化。 与深度图或体素相比,点云和网格表示 3D 空间中的非结构化数据。点由它们的 (X, Y, Z) 坐标表示,在 3D 空间中可能彼此靠近的两个点在数组表示中可能很远。与2d图像中的相同问题相比,理解某个点的邻域并不是一项简单的任
K-Nearest-Neighbours 和 kd 树
什么是KNN? KNN算法是没有学习过程的。它将所有已知数据存储起来,当要预测某一新数据时,使用某种距离度量选择离该新数据在特种空间中最近的K个点,根据分类决策规则,一般是多数投票规则对新数据进行分类。 怎样构造KNN: 1) 距离度量 LP距离。在P=1时是曼哈顿距离,P=2时是欧式距离,P为无穷大时是切比雪夫距离。也可以自己定义距离。 2)K值选择 K只选择太小,容易过拟合





![KD_Tree 【bzoj2648 bzoj2716】SJY摆棋子 [voilet 3] 天使玩偶](/front/images/it_default.gif)