本文主要是介绍KD-Trees(K-dimensional树)和Octrees(八叉树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
KD-Trees(K-dimensional树)和Octrees(八叉树)是两种常用的数据结构,它们在多维空间中用于高效地存储和查询数据。这两种结构在计算机科学中有着广泛的应用,尤其是在图形学、机器人学、空间索引和最近邻搜索等领域。
KD-Trees
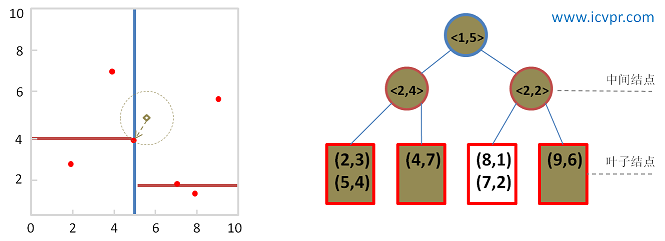
KD-Trees是一种二叉树结构,用于组织K维空间中的点。在KD-Trees中,每个节点代表一个K维空间中的点,并且树是通过递归地将空间分割成两部分来构建的。分割是通过在每个维度上交替选择一个维度,并在这个维度上选择一个分割点来完成的。
构建过程:
- 选择一个维度作为分割维度。通常选择方差最大的维度,以确保分割尽可能均匀。
- 在选定的维度上选择一个分割点,通常是该维度上的中位数点,以保持树的平衡。
- 将所有小于分割点的点放在左子树,大于分割点的点放在右子树。
- 对左右子树重复上述过程,直到所有点都被分配到叶子节点。
应用:
- 最近邻搜索:在KD-Trees中查找最近邻点可以有效地减少搜索空间。
- 范围查询:查找位于特定多维矩形内的所有点。
Octrees
Octrees是一种树状数据结构,用于组织三维空间中的点。每个节点最多有八个孩子,对应于将空间分割成八个卦限(octants)。Octrees通过递归地将空间分割成八个卦限来构建,直到达到某个预定的深度或每个卦限中的点数小于某个阈值。
构建过程:
- 将整个空间视为根节点。
- 如果节点包含的点数超过阈值,或者达到最大深度,则停止分割。
- 否则,将空间分割成八个卦限,并为每个卦限创建一个子节点。
- 将点分配到相应的卦限中,对每个子节点重复上述过程。
应用:
- 空间划分:在三维图形学中,用于加速光线追踪和碰撞检测。
- 体素化:在医学成像和科学可视化中,用于表示和处理三维数据集。
- 动态场景管理:在游戏和机器人导航中,用于高效地管理动态对象和环境。
总结
KD-Trees和Octrees都是用于高效处理多维空间数据的数据结构。KD-Trees适用于任意维度的空间,而Octrees专门用于三维空间。两者都通过递归分割空间来组织数据,从而支持高效的查询操作,如最近邻搜索和范围查询。在实际应用中,选择哪种数据结构取决于具体的需求和数据特性。
这篇关于KD-Trees(K-dimensional树)和Octrees(八叉树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!