四叉树和KD树

2024-06-15 02:52
文章标签 四叉树 kd

本文主要是介绍四叉树和KD树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 简介

四叉树和KD树都是用于空间数据索引和检索的树状数据结构。它们通过将空间递归地划分为更小的区域，并存储每个区域内的点，来实现快速搜索和范围查询。

2. 四叉树

2.1 定义

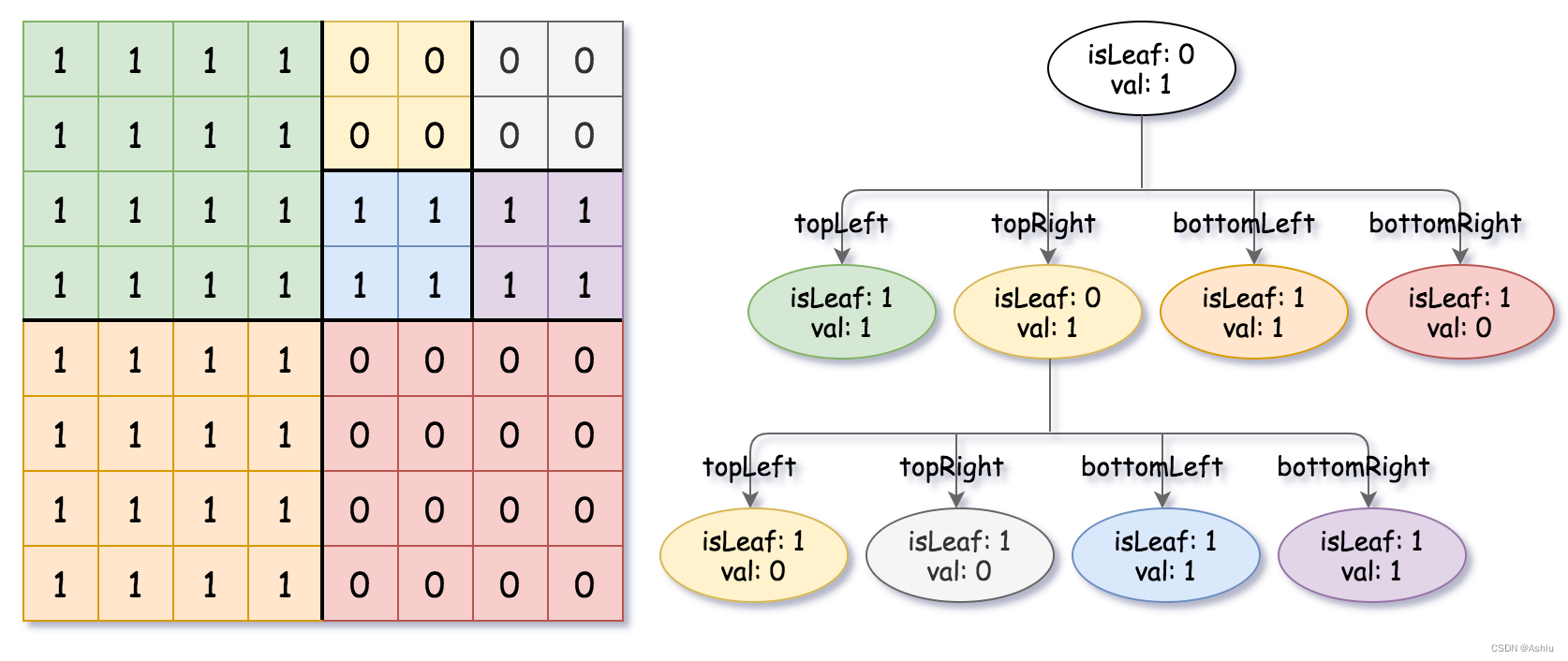
四叉树是一种树状数据结构，它将二维空间递归地划分为四个相等的子区域，直到每个子区域只包含一个点或为空。每个节点代表一个矩形区域，并存储该区域内的所有点。

2.2 构建

构建四叉树的过程如下：

  1. 将整个空间划分为四个相等的子区域。
  2. 将每个点分配到相应的子区域。
  3. 递归地对每个子区域进行步骤 1 和 2，直到每个子区域只包含一个点或为空。

2.3 搜索

搜索四叉树的过程如下：

  1. 从根节点开始，检查当前节点的区域是否包含目标点。
  2. 如果包含，则递归地搜索该节点的四个子节点。
  3. 如果不包含，则搜索失败。

2.4 范围查询

范围查询是指查找所有位于给定矩形区域内的点。搜索过程与搜索单个点类似，但需要遍历所有与查询区域相交的节点。

2.5 Kotlin 代码演示


data class Point(val x: Double, val y: Double)data class Rectangle(val x: Double, val y: Double, val width: Double, val height: Double) {fun contains(point: Point): Boolean {return point.x >= x && point.x <= x + width && point.y >= y && point.y <= y + height}fun intersects(other: Rectangle): Boolean {return !(other.x + other.width < x ||other.x > x + width ||other.y + other.height < y ||other.y > y + height)}
}class QuadTree(val boundary: Rectangle, val capacity: Int = 1) {private var points: MutableList<Point> = mutableListOf()private var children: Array<QuadTree?> = arrayOfNulls(4)fun insert(point: Point): Boolean {if (!boundary.contains(point)) {return false}if (points.size < capacity) {points.add(point)return true}if (children[0] == null) {subdivide()}for (i in 0..3) {if (children[i]!!.insert(point)) {return true}}return false}private fun subdivide() {val xMid = boundary.x + boundary.width / 2val yMid = boundary.y + boundary.height / 2children[0] = QuadTree(Rectangle(boundary.x, boundary.y, xMid, yMid), capacity)children[1] = QuadTree(Rectangle(xMid, boundary.y, boundary.x + boundary.width, yMid), capacity)children[2] = QuadTree(Rectangle(boundary.x, yMid, xMid, boundary.y + boundary.height), capacity)children[3] = QuadTree(Rectangle(xMid, yMid, boundary.x + boundary.width, boundary.y + boundary.height), capacity)for (point in points) {for (i in 0..3) {if (children[i]!!.insert(point)) {break}}}points.clear()}fun query(range: Rectangle): List<Point> {val foundPoints = mutableListOf<Point>()if (!boundary.intersects(range)) {return foundPoints}for (point in points) {if (range.contains(point)) {foundPoints.add(point)}}if (children[0] != null) {for (child in children) {if (child != null) {foundPoints.addAll(child.query(range))}}}return foundPoints}
}fun main() {val boundary = Rectangle(0.0, 0.0, 10.0, 10.0)val quadTree = QuadTree(boundary, 4)val points = listOf(Point(1.0, 1.0),Point(2.0, 2.0),Point(3.0, 3.0),Point(4.0, 4.0),Point(5.0, 5.0),Point(6.0, 6.0),Point(7.0, 7.0),Point(8.0, 8.0),Point(9.0, 9.0))for (point in points) {quadTree.insert(point)}val queryRange = Rectangle(0.0, 0.0, 5.6, 4.4)val foundPoints = quadTree.query(queryRange)println("Points in range:")for (point in foundPoints) {println("(${point.x}, ${point.y})")}
}

3. KD树

3.1 定义

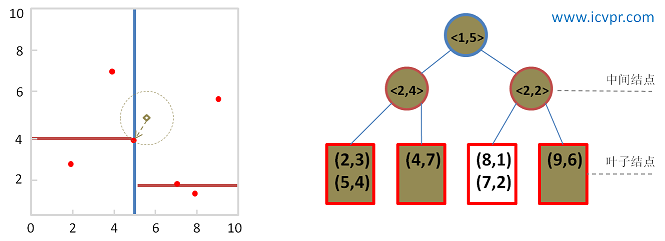
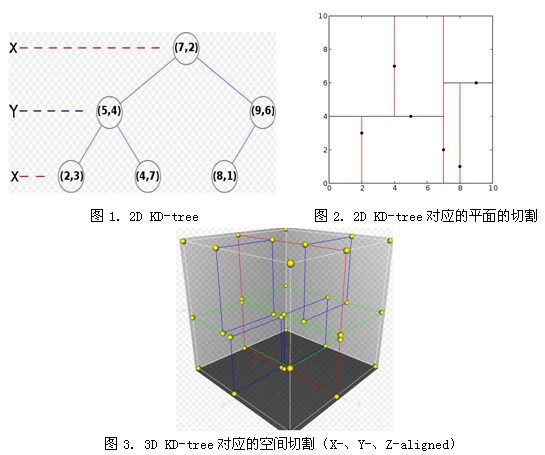
KD树是一种树状数据结构，它将多维空间递归地划分为两个子空间，每个子空间由一个超平面分割。每个节点代表一个超矩形区域，并存储该区域内的所有点。

3.2 构建

构建KD树的过程如下：

  1. 选择一个维度作为分割维度，并找到该维度上的中位数。
  2. 使用中位数将空间划分为两个子空间。
  3. 递归地对每个子空间进行步骤 1 和 2，直到每个子空间只包含一个点或为空。

3.3 搜索

搜索KD树的过程如下：

  1. 从根节点开始，检查当前节点的区域是否包含目标点。
  2. 如果包含，则根据目标点的坐标选择相应的子节点进行递归搜索。
  3. 如果不包含，则搜索失败。

3.4 范围查询

范围查询是指查找所有位于给定超矩形区域内的点。搜索过程与搜索单个点类似，但需要遍历所有与查询区域相交的节点。

3.5 Kotlin 代码演示


// Define the Point class
internal class Point(var x: Double, var y: Double) {override fun toString(): String {return "($x, $y)"}
}// Define the k-d tree node class
internal class KDNode(var point: Point) {var left: KDNode? = nullvar right: KDNode? = null
}// Define the k-d tree class
internal class KDTree(points: List<Point>) {private val root: KDNode?init {this.root = buildTree(points, 0)}private fun buildTree(points: List<Point>, depth: Int): KDNode? {if (points.isEmpty()) {return null}val axis = depth % Kval sortedPoints = points.sortedWith(Comparator { a, b ->if (axis == 0) {a.x.compareTo(b.x)} else {a.y.compareTo(b.y)}})val medianIndex = sortedPoints.size / 2val node = KDNode(sortedPoints[medianIndex])node.left = buildTree(sortedPoints.subList(0, medianIndex), depth + 1)node.right = buildTree(sortedPoints.subList(medianIndex + 1, sortedPoints.size), depth + 1)return node}fun rangeSearch(lowerLeft: Point, upperRight: Point): List<Point> {val result: MutableList<Point> = ArrayList()rangeSearch(root, lowerLeft, upperRight, 0, result)return result}private fun rangeSearch(node: KDNode?,lowerLeft: Point,upperRight: Point,depth: Int,result: MutableList<Point>) {if (node == null) {return}val point = node.pointif (point.x >= lowerLeft.x && point.x <= upperRight.x && point.y >= lowerLeft.y && point.y <= upperRight.y) {result.add(point)}val axis = depth % Kif (axis == 0) {if (lowerLeft.x <= point.x) {rangeSearch(node.left, lowerLeft, upperRight, depth + 1, result)}if (upperRight.x >= point.x) {rangeSearch(node.right, lowerLeft, upperRight, depth + 1, result)}} else {if (lowerLeft.y <= point.y) {rangeSearch(node.left, lowerLeft, upperRight, depth + 1, result)}if (upperRight.y >= point.y) {rangeSearch(node.right, lowerLeft, upperRight, depth + 1, result)}}}companion object {private const val K = 2 // 2-dimensional space, e.g., x, y, z, t, etc}
}// Example usage
object KDTreeExample {@JvmStaticfun main(args: Array<String>) {val points: MutableList<Point> = ArrayList()points.add(Point(0.5, 0.5))points.add(Point(1.0, 1.0))points.add(Point(1.5, 1.5))points.add(Point(2.0, 2.0))points.add(Point(3.0, 3.0))val kdTree = KDTree(points)val lowerLeft = Point(0.0, 0.0)val upperRight = Point(1.5, 2.2)val result = kdTree.rangeSearch(lowerLeft, upperRight)for (point in result) {println(point)}}
}

5. 注意事项

  • 四叉树和KD树的构建和搜索时间复杂度取决于数据的分布和查询区域的大小。
  • 四叉树和KD树都是用于空间数据索引和检索的有效数据结构。四叉树适用于二维空间，而KD树适用于多维空间。
  • 在实际应用中，可以使用各种优化技术来提高性能，例如使用边界框、预分配内存等。
  • 对于高维数据，KD树的性能可能会下降，可以使用其他数据结构，例如球树或随机投影树。

这篇关于四叉树和KD树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1062228。

相关文章

四叉树算法

四叉树算法

1、主要推荐英文文章阅读地址：https://gamedevelopment.tutsplus.com/tutorials/quick-tip-use-quadtrees-to-detect-likely-collisions-in-2d-space--gamedev-374 附带碰撞检测英文文章章阅读地址：https://gamedevelopment.tutsplus.com/tutoria
阅读更多...
kd-tree理论以及在PCL 中的代码的实现

kd-tree理论以及在PCL 中的代码的实现

(小技巧记录：博客园编辑的网页界面变小了使用Ctrl  ++来变大网页字体) 通过雷达，激光扫描，立体摄像机等三维测量设备获取的点云数据，具有数据量大，分布不均匀等特点，作为三维领域中一个重要的数据来源，点云主要是表征目标表面的海量点的集合，并不具备传统网格数据的几何拓扑信息，所以点云数据处理中最为核心的问题就是建立离散点间的拓扑关系，实现基于邻域关系的快速查找。 k-d树 （k-dime
阅读更多...
KD-Tree 的一些理解--

KD-Tree 的一些理解--

阅读文档：Wikipedia 上的 KD Tree 。 https://en.wikipedia.org/wiki/K-d_tree 引言 In computer science, a k-d tree (short for k-dimensional tree) is a space-partitioning data structure for organizing points in a
阅读更多...
【C++PCL】点云处理Kd-tree原理

【C++PCL】点云处理Kd-tree原理

作者：迅卓科技 简介：本人从事过多项点云项目，并且负责的项目均已得到好评！ 公众号：迅卓科技，一个可以让您可以学习点云的好地方 重点：每个模块都有参数如何调试的讲解，即调试某个参数对结果的影响是什么，大家有问题可以评论哈，如果文章有错误的地方，欢迎来指出错误的地方。 目录         1.原理介绍 1.原理介绍         kd-tree是散乱点云的一种储存结构，它是一种
阅读更多...
KD-TREE 算法原理

KD-TREE 算法原理

KD-TREE 算法原理 http://www.oneie.com/index.php/qyjs/47-txcl/1532-kd-tree   本文介绍一种用于高维空间中的快速最近邻和近似最近邻查找技术——Kd- Tree（Kd树）。Kd-Tree，即K-dimensional tree，是一种高维索引树形数据结构，常用于在大规模的高维数据空间进行最近邻查找(Nearest Neighbor
阅读更多...
KD Tree

KD Tree

转载地址：http://www.cnblogs.com/slysky/archive/2011/11/08/2241247.html KD Tree Kd-树 其实是K-dimension tree的缩写，是对数据点在k维空间中划分的一种数据结构。其实，Kd-树是一种平衡二叉树。 举一示例： 假设有六个二维数据点 = {（2,3），（5,4），（9,6），（4,7），（8,1）
阅读更多...
机器学习--从K近邻算法、距离度量谈到KD树、SIFT+BBF算法

机器学习--从K近邻算法、距离度量谈到KD树、SIFT+BBF算法

引言     最近在面试中，除了基础 &  算法 & 项目之外，经常被问到或被要求介绍和描述下自己所知道的几种分类或聚类算法(当然，这完全不代表你将来的面试中会遇到此类问题，只是因为我的简历上写了句：熟悉常见的聚类 & 分类算法而已)，而我向来恨对一个东西只知其皮毛而不得深入，故写一个有关数据挖掘十大算法的系列文章以作为自己备试之用，甚至以备将来常常回顾思考。行文杂乱，但侥幸若能对读者起到一
阅读更多...
史上最详细四叉树地图不同技术应用和代码详解

史上最详细四叉树地图不同技术应用和代码详解

四叉树地图在计算机和机器人领域应用的很广，但是初学者可能会发现四叉树地图有各种不同的实现方式，很多在机器人领域不适用或是在计算机存储领域不适用。今天我就讲解下各类四叉树的实现方式和应用场景。 史上最详细四叉树地图不同技术应用和代码详解 本文禁止转载，主要是为了有不同见解的同学可以方便联系我，我的邮箱 fanzexuan135@163.com 四叉树地图:应用与研究综述 1. 引言 四叉树地图
阅读更多...
427. 建立四叉树

427. 建立四叉树

427. 建立四叉树 题目难度-中等1. dfs分治 题目难度-中等 给你一个 n * n 矩阵 grid ，矩阵由若干 0 和 1 组成。请你用四叉树表示该矩阵 grid 。 你需要返回能表示矩阵 grid 的 四叉树 的根结点。 四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性： val：储存叶子结点所代表的区域的值。1 对应 True，0 对应
阅读更多...
KD-Trees（K-dimensional树）和Octrees（八叉树

KD-Trees（K-dimensional树）和Octrees（八叉树

KD-Trees（K-dimensional树）和Octrees（八叉树）是两种常用的数据结构，它们在多维空间中用于高效地存储和查询数据。这两种结构在计算机科学中有着广泛的应用，尤其是在图形学、机器人学、空间索引和最近邻搜索等领域。 KD-Trees KD-Trees是一种二叉树结构，用于组织K维空间中的点。在KD-Trees中，每个节点代表一个K维空间中的点，并且树是通过递归地将空间分割成两
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2