本文主要是介绍机器学习之深入理解K最近邻分类算法(K Nearest Neighbor),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【机器学习】《机器学习实战》读书笔记及代码:第2章 - k-近邻算法
1、初识
K最近邻分类算法(K Nearest Neighbor)是著名的模式识别统计学方法,在机器学习分类算法中占有相当大的地位。主要应用领域是对未知事物的识别,即推断未知事物属于哪一类。
推断思想是,基于欧几里得定理,推断未知事物的特征和哪一类已知事物的的特征最接近。简单来说就是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
KNN 算法本身简单有效,它是一种 lazy-learning 算法,分类器不需要使用训练集进行训练,训练时间复杂度为0。KNN 分类的计算复杂度和训练集中的文档数目成正比,也就是说,如果训练集中文档总数为 n,那么 KNN 的分类时间复杂度为O(n)。
KNN方法尽管从原理上也依赖于极限定理,但在类别决策时,仅仅与极少量的相邻样本有关。因为KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其它方法更为适合。
2、不惑
该算法涉及3个主要因素:实例集、距离或相似的衡量、K的大小。
一个实例的K最近邻是根据标准欧氏距离定义的。更精确地讲,把任意的实例集 x 表示为下面的特征向量:
< a 1 ( x ) , a 2 ( x ) , a 3 ( x ) , . . . , a n ( x ) > <a_{1}(x),a_{2}(x),a_{3}(x),...,a_{n}(x)> <a1(x),a2(x),a3(x),...,an(x)>
其中 a r ( x ) a_{r}(x) ar(x)表示是实例集 x 对的第 r 个属性值,那么两个实例 x i x_{i} xi和 x j x_{j} xj的距离定义为 d ( x i , x j ) d(x_{i},x_{j}) d(xi,xj),公式为:
∑ r = 1 n [ a r ( x i − x j ) ] 2 \sqrt{\sum_{r = 1}^{n}[a_{r}(x_{i} - x_{j})]^{2}} r=1∑n[ar(xi−xj)]2
有关KNN算法的几点说明:
- 在K最近邻学习中,目标函数值可以为离散值,也可以为实值。
- 我们先考虑学习以下形式的离散目标函数: f : ℜ n ⟶ V f:\Re^{n} \longrightarrow V f:ℜn⟶V,其中V是有限集合 { v 1 , . . . , v s } \{v_{1},...,v_{s}\} {v1,...,vs}。下表给出了逼近离散目标函数的K近邻算法。
- 正如下表中所指出的,这个算法的返回值 f ′ ( x q ) f^{′}(x_{q}) f′(xq)为对 f ( x q ) f(x_{q}) f(xq)的估计,它就是距离 x q x_{q} xq最近的k个训练样例中最普遍的f值。
- 如果我们选择k=1,那么“1近邻算法”就把 f ( x i ) f(x_{i}) f(xi)赋给 ( x q ) (x_{q}) (xq),其中xi是最靠近 x q x_{q} xq的训练实例。对于较大的k值,这个算法返回前k个最靠近的训练实例中最普遍的f值。
逼近离散值函数f: Ân - V的K近邻算法

3、洞玄
例子1)
KNN能够说是一种最直接的用来分类未知数据的方法。下面通过图和文字明确说明K-NN是干什么的。
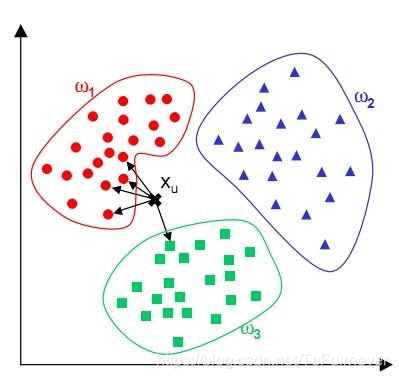
简单来说,KNN算法中,所选择的邻居都是已经正确分类的对象(红色、蓝色、绿色),该算法在定类决策上仅仅根据最邻近的K个样本的类别来决定待分样本所属的类别。
例子2)
如下图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。也就是说,现在, 我们不知道中间那个绿色的数据是从属于哪一类(蓝色小正方形or红色小三角形),下面,我们就要解决这个问题:给这个绿色的圆分类。

-
如果K=3,绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
-
如果K=5,绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
我们可以看出,当无法判定当前待分类点是从属于已知分类中的哪一类时,我们可以依据统计学的理论看它所处的位置特征,衡量它周围邻居的权重,而把它归为(或分配)到权重更大的那一类。
例子3)
下图图解了一种简单情况下的K近邻算法,在这里实例是二维空间中的点,目标函数具有布尔值。正反训练样例用“+”和“-”分别表示。图中也画出了一个查询点 x q x_{q} xq。注意在这幅图中,1近邻算法把 x q x_{q} xq分类为正例,然而5近邻算法把 x q x_{q} xq分类为反例。
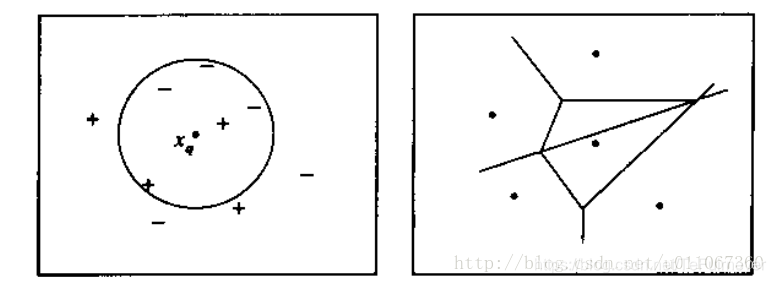
图解说明:
左图画出了一系列的正反训练样例和一个要分类的查询实例 x q x_{q} xq。1近邻算法把 x q x_{q} xq分类为正例,然而5近邻算法把 x q x_{q} xq分类为反例。
右图是对于一个典型的训练样例集合1近邻算法导致的决策面。围绕每个训练样例的凸多边形表示最靠近这个点的实例空间(即这个空间中的实例会被1-近邻算法赋予该训练样例所属的分类)。
对前面的k邻算法作简单的修改后,它就可被用于逼近连续值的目标函数。为了实现这一点,我们让算法计算k个最接近样例的平均值,而不是计算其中的最普遍的值。更精确地讲,为了逼近一个实值目标函数,我们只要把算法中的公式替换为:

4、知命
kNN算法因其提出时间较早,随着其他技术的不断更新和完善,kNN算法的诸多不足之处也逐渐显露,因此许多kNN算法的改进算法也应运而生:
-
快速KNN算法。参考FKNN论述文献(实际应用中结合lucene)。
-
加权欧氏距离公式。在传统的欧氏距离中,各特征的权重相同,也就是认定各个特征对于分类的贡献是相同的,显然这是不符合实际情况的,并且使得特征向量之间相似度计算不够准确,进而影响分类精度。加权欧氏距离公式,特征权重通过灵敏度方法获得(根据业务需求调整,例如关键字加权、词性加权等)。
下面举一个例子,比如距离加权最近邻算法,根据它们相对查询点 x q x_{q} xq的距离,将较大的权值赋给较近的近邻。在上表逼近离散目标函数的算法中,我们可以根据每个近邻与 x q x_{q} xq的距离平方的倒数加权这个近邻的“选举权”。
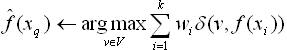
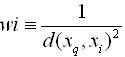
为了处理查询点 x q x_{q} xq恰好匹配到某个训练样例 x i x_{i} xi,从而导致分母为0的情况,我们令这种情况下的 f ′ ( x q ) f '(x_{q}) f′(xq)等于 f ( x i ) f(x_{i}) f(xi)。如果有多个这样的训练样例,则我们使用它们中占多数的分类。
我们也可以用类似的方式对实值目标函数进行距离加权,只要用下式替换上表的公式:
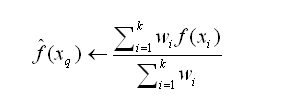
其中wi的定义与之前公式中相同:
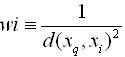
注意这个公式中的分母是一个常量,它将不同权值的贡献归一化(例如,它保证如果对所有的训练样例 x i x_{i} xi, f ( x i ) = c f(x_{i})=c f(xi)=c,那么 ( x q ) < − − c (x_{q})<--c (xq)<−−c)。
注意以上k近邻算法的所有变体都只考虑k个近邻以分类查询点。
如果使用按距离加权,那么允许所有的训练样例影响 x q x_{q} xq的分类,事实上这没有坏处,因为非常远的实例对 ( x q ) (x_{q}) (xq)的影响很小。考虑所有样例的惟一不足是会使分类运行得更慢。如果分类一个新的查询实例时考虑所有的训练样例,我们称此为全局(global)法。如果仅考虑最靠近的训练样例,我们称此为局部(local)法。
5、天启
-
算法优点:简单、易于理解、容易实现、通过对K的选择可具备丢噪音数据的健壮性
-
算法缺点:
- 训练耗时短,测试耗时长。训练的时候仅需记忆所有数据即可,如果是传递指针的话,能够常数时间内完成 O(1)。
- 需要大量的空间储存已知的实例、算法的复杂度高(需要比较所有已知实例与要分类的实例)。
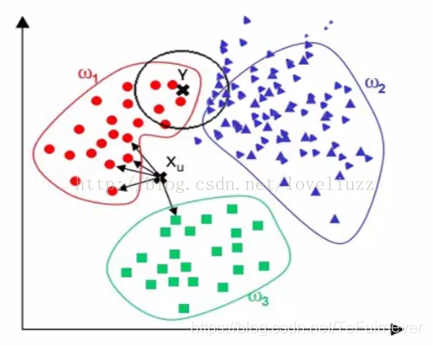
- 当样本分布不均衡时,比如其中一类样本过大(实例数据量过多)占主导的时候,新的未知实例容易被归类为这个主导样本,因为这类样本实例的数量过大,但这个新的未知实例实际并未接近目标样本,如下图:
- 两点间距离公式不能提供足够的信息,比如:【CS231n】斯坦福大学李飞飞视觉识别课程笔记(五):图像分类笔记(下)
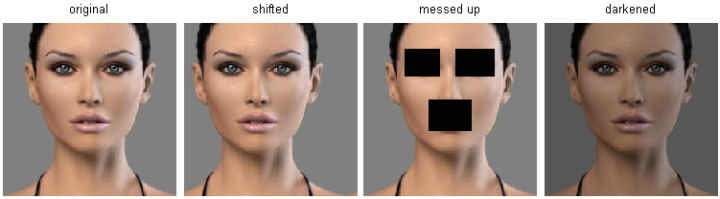
图中右侧的三张图片是在左侧图片上分别作出了某些修改后形成的,而通过精心的构建,这三张图片与左侧原本的图片有相同的距离,也就是说距离公式无法将他们区分开。而事实上,如果进行精心的设计,我们甚至可以让任意两张修改后的图片都与某张照片具有相同的距离。 - 维度灾难。为了能够有效的体现出K最近邻分类算法(K Nearest Neighbor)的“最邻近”这个概念,我们势必需要样本能够均匀的分布在整个空间中,将整个空间支撑起来。在一维或者二维的情况下还好说,如果假设一维需要4个样本点,那么二维需要16个样本点,而到了三维就需要64个样本点。所需的样本数量随着维数的增加呈现指数级增长的趋势,这无疑是灾难性的,所以被称作“维度灾难”。我们一张图片就算很小,10像素*10像素,再乘上RGB三个颜色值,一共有300个数值,这就意味着300维度,而 4 300 4^{300} 4300 是一个无法想象的天文数字,我们永远不可能取得足够多的数据。
6、无距
用空间内两个点的距离来度量。距离越大,表示两个点越不相似。距离的选择有很多,通常用比较简单的欧式距离。
欧式距离:
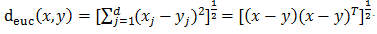
马氏距离:马氏距离能够缓解由于属性的线性组合带来的距离失真,是数据的协方差矩阵。
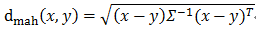
曼哈顿距离:
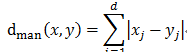
切比雪夫距离:
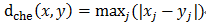
闵氏距离:r取值为2时:曼哈顿距离;r取值为1时:欧式距离。
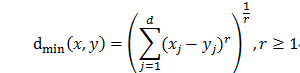
平均距离:
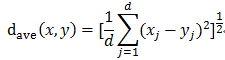
弦距离:

测地距离:
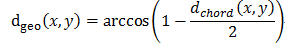
7、无矩
《算法图解》学习笔记(十):K 最近邻算法(附代码)
如果想要更多的资源,欢迎关注 @我是管小亮,文字强迫症MAX~
回复【福利】即可获取我为你准备的大礼,包括C++,编程四大件,NLP,深度学习等等的资料。
想看更多文(段)章(子),欢迎关注微信公众号「程序员管小亮」~

参考文章
- 机器学习——最邻近规则分类(K Nearest Neighbor)KNN算法
- 参考文章——KNN(k-nearest neighbor的缩写)最近邻算法原理详解
- CS231n 2017 学习笔记01——KNN(K-Nearest Neighbors)
- KNN邻近分类算法
- 机器学习与数据挖掘-K最近邻(KNN)算法的实现(java和python版)
这篇关于机器学习之深入理解K最近邻分类算法(K Nearest Neighbor)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








