morris专题
KMP(Knuth-Morris-Pratt)算法
一、朴素匹配算法 也就是暴力匹配算法。设匹配字符串的长度为n,模式串的长度为m,在最坏情况下,朴字符串匹配算法运行时间为O((n - m + 1)m)。如果m = n / 2, 那么该算法的复杂度就是Θ(n ^ 2)。由于不需要预处理,朴素字符串匹配算法运行时间即为其匹配时间。 strstr()函数就可以用这个方法实现,尽管效率不高: //strstr函数char *strS
Morris遍历-二叉树遍历空间复杂度O(1)
一、什么是Morris遍历? 在介绍啊Morris遍历之前,先提一嘴二叉树的遍历,先序,中序,后续,相信大家都写过。 我们如果把打印行为,放在 1 位置,就是先序遍历,放在2位置就是中序遍历,放在3位置就是后序遍历。相信大家经常这样写。这种方式,对于一个节点,会回到三次,所以二叉树的遍历时间复杂度为O(n),这个n是什么,二叉树节点的个数,用这种方式实现二叉树遍历,额外空间复杂度是多少,对
Morris遍历二叉树(非递归,不用栈,O(1)空间)
一、概述 实现二叉树的前中后序遍历,达到要求: O(1)空间复杂度,即只能使用常数空间;二叉树的形状不能被破坏(中间过程允许改变其形状)。 二、代码详解 /*** Morris遍历* @author superman**/public class MorrisTraversal {public static void process(Node head) {if(head == null
Morris Traversal-常量空间下遍历二叉树
通常遍历二叉树有前序(preorder)、中序(inorder)、后序(postorder)遍历有两个常用的方法:一是递归(recursive),二是使用栈实现的迭代版本(stack+iterative)。这两种方法都是O(n)的空间复杂度(递归本身占用stack空间或者用户自定义的stack)。递归的方法很简单,栈使用的方法见楼主另一篇文章,栈和队列在遍历二叉树中的使用。文章总结了常见的几种思路
KMP(Knuth-Morris-Pratt)算法详解及C++代码实现
在计算机科学中,字符串匹配是一个基础且重要的任务。给定一个主字符串(也称为文本)和一个模式字符串(也称为词),字符串匹配算法的任务是在主字符串中查找与模式字符串相同的子串,并返回其位置。Knuth-Morris-Pratt(KMP)算法是一种高效的字符串匹配算法,由D.E. Knuth、J.H. Morris和V.R. Pratt联合提出。该算法通过减少不必要的字符比较次数,从而提高了字符串匹配的
字符串匹配的KMP算法(The Knuth-Morris-Pratt Algorithm)
前言 字符串匹配是计算机的基本任务之一。 KMP算法的思想 1. 首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。 2. 因为B与A不匹配,搜索词再往后移。 3. 就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。 4.接着比较字符串和搜索词
数学小课堂:字符串匹配算法KMP(The Knuth-Morris-Pratt Algorithm)
文章目录 前言I KMP算法1.1 思想1.2 代码实现 II《部分匹配表》是如何产生的?2.1 "前缀"和"后缀"2.2 以"ABCDABD"为例,2.3 "部分匹配"的实质 see also 前言 字符串匹配是计算机的基本任务之一。 KMP算法的思想是,设法利用已知的匹配信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。 做法:针对搜索词,算
LeetCode题目99:图解中叙遍历、Morris遍历实现恢复二叉树搜索树【python】
题目描述 给你二叉搜索树的根节点 root,该树中的恰好两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树。 输入格式 root:二叉树的根节点。 输出格式 不需要返回值,直接在原树上进行恢复。 示例 示例 1 输入: [1,3,null,null,2]输出: [3,1,null,null,2]解释: 3 和 1 被错误交换。 示例 2 输入: [3,1,4,
业界瞩目:合规专家Graham Morris加盟ATFX,开启战略新篇章
又一重磅人才加盟ATFX。3月22日,ATFX宣布一项新任命,任命格雷厄姆·莫里斯(Graham Morris)为澳大利亚业务的合规主管。莫里斯将为公司带来丰富的合规专业知识和行业经验,对于提升ATFX的监管框架并监督澳大利亚金融市场内的合规事务将发挥关键作用。 莫里斯以辉煌的职业背景加入ATFX,此前他曾担任 OANDA 澳大利亚和 OANDA 全球市场 (BVI) 的合规主管。他在任职期间
KMP(Knuth-Morris-Pratt)算法,详细版
KMP(Knuth-Morris-Pratt)算法 1、KMP算法 在目标串T中搜索模式串P 由于强制算法(暴力搜素算法)在找到不匹配的字符时,只能把模式串P(相对于目标串T)移动一个位置,导致大量的操作重复,冗余的次数随目标串,或模式串长度的增长,使得代码的执行效率直线下降。 为了使搜素的效率提高,且不遗漏每一处匹配,KMP算法通过利用匹配失败处的位置信息,进行改进,使失败的
数据结构-KMP 算法(Knuth-Morris-Pratt 字符串查找算法)
1.什么是KMP算法:快速的从一个主串中找出一个你想要的子串 KMP算法是一种改进的字符串匹配算法。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。 首先,对于这个问题有一个很单纯的想法:从左到右一个个匹配,如果这个过程
一篇优质的Knuth-Morris-Pratt算法讲解
文章目录 部分匹配表如何使用部分匹配表 部分匹配表 KMP的关键是部分匹配表。我和理解KMP之间的主要障碍是我没有完全理解部分匹配表中的值的真正含义。我现在将尽可能用最简单的话来解释它们。 下面是模式“ABABABACA”的部分匹配表: 如果我有一个八个字符的模式(在本例的持续时间内,让我们说“abababca”),我的部分匹配表将有八个单元格。如果我看表中的第八个也是最后
KMP 算法(Knuth–Morris–Pratt algorithm)的基本思想
KMP 算法(Knuth–Morris–Pratt algorithm)的基本思想 阅读本文之前,您最好能够了解 KMP 算法解决的是什么问题,最好能用暴力方式(Brute Force)解决一下该问题。 KMP 算法主要想解决的是文本搜索的问题: 给定一个模式字符串 p 和一个子串 t, 找出 p 串出现在 t 串中的位置。 术语定义 "abc"(引号中的字符串): 代表字符串
[算法系列之十四]字符串匹配之Morris-Pratt字符串搜索算法
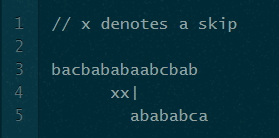
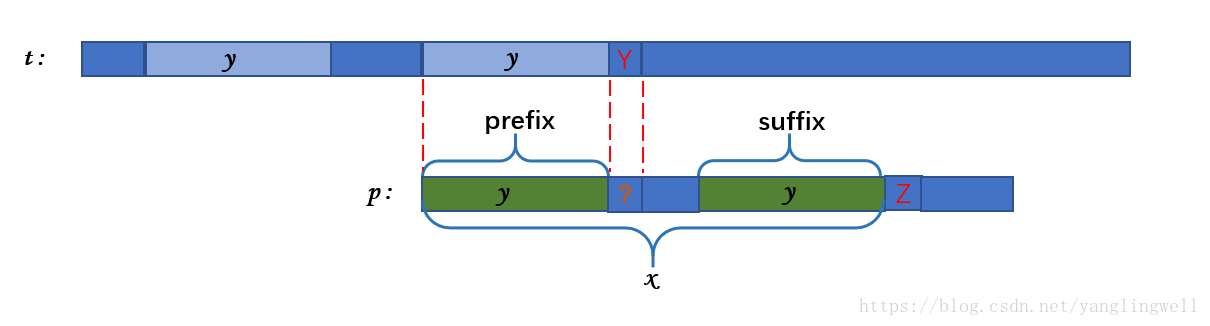
前言 我们前面已经看到,蛮力字符串匹配算法和Rabin-Karp字符串匹配算法均非有效算法。不过,为了改进某种算法,首先需要详细理解其基本原理。我们已经知道,暴力字符串匹配的速度缓慢,并已尝试使用Rabin-Karp中的一个散列函数对其进行改进。问题是,Rabin-Karp的复杂度与强力字符串匹配相同,均为O(mn)。 我们显然需要采用一种不同方法,但为了提出这种不同方法,先来看看暴力字符串匹
字符串匹配算法--KMP字符串搜索(Knuth–Morris–Pratt string-searching)C语言实现与讲解
一、前言 在计算机科学中,Knuth-Morris-Pratt字符串查找算法(简称为KMP算法)可在一个主文本字符串S内查找一个词W的出现位置。此算法通过运用对这个词在不匹配时本身就包含足够的信息来确定下一个匹配将在哪里开始的发现,从而避免重新检查先前匹配的字符。这个算法是由高德纳和沃恩·普拉特在1974年构思,同年詹姆斯·H·莫里斯也独立地设计出该算法,最终由三人于1977年联合发表。(
Morris Traversal方法遍历二叉树(非递归,不用栈,O(1)空间,修改二叉树)
本文主要解决一个问题,如何实现二叉树的前中后序遍历,有两个要求: 1. O(1)空间复杂度,即只能使用常数空间; 2. 二叉树的形状不能被破坏(中间过程允许改变其形状)。 通常,实现二叉树的前序(preorder)、中序(inorder)、后序(postorder)遍历有两个常用的方法:一是递归(recursive),二是使用栈实现的迭代版本(stack+iterative)。这两种
Knuth-Morris-Pratt算法
记录一篇讲的比较好的KMP算法链接,以便下次访问: 链接1: https://blog.csdn.net/u013074465/article/details/46637239?locationNum=5&fps=1 链接2: http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorith
“Morris II.“的AI病毒悄然登场
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领域的领跑者。点击订阅,与未来同行! 订阅:https://rengongzhineng.io/ 最近,一个由科技前沿的研究团队开发的名为“莫里斯二代”的AI蠕虫引起了广
LeetCode 501. 二叉搜索树中的众数(Morris中序遍历)
Morris 中序遍历 用 Morris 中序遍历的方法把中序遍历的空间复杂度优化到 O(1) Morris 中序遍历的一个重要步骤就是寻找当前节点的前驱节点,并且 Morris 中序遍历寻找下一个点始终是通过转移到 \rm rightright 指针指向的位置来完成的。 如果当前节点没有左子树,则遍历这个点,然后跳转到当前节点的右子树。如果当前节点有左子树,那么它的前驱节点一定在左子树
(含morris遍历)代码随想录 Leetcode144/94/145 二叉树的前/中/后序遍历
题目: 前: 中: 后: 代码(首刷自解 2024年1月24日): //前序遍历,递归class Solution {public:void funcOfRecursion(TreeNode* cur, vector<int>& vec) {if (cur == nullptr) return;vec.emplace_back(cur->val);funcOfRe
【leetcode系列】【算法】【中等】二叉树的中序遍历(递归,栈,莫里斯morris)
目录 题目: 解题思路: 方法一:递归(时间O(N),空间O(N)) 方法二:栈(时间O(N),空间O(N)) 方法三:莫里斯遍历(时间O(N),空间O(1)) 解题思路: 方法一:递归 方法二:栈 方法三:莫里斯 题目: 题目链接: https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
morris前序遍历
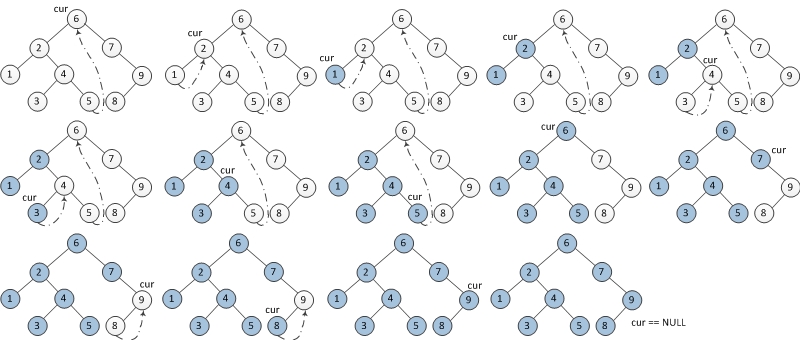
实现原理: 记作当前节点为cur。 如果cur无左孩子,cur向右移动(cur=cur.right)如果cur有左孩子,找到cur左子树上最右的节点,记为mostright 如果mostright的right指针指向空,让其指向cur,cur向左移动(cur=cur.left)如果mostright的right指针指向cur,让其指向空,cur向右移动(cur=cur.right) #i
左神算法:遍历二叉树的神级方法(Morris遍历 / 线索二叉树)
本题来自左神《程序员代码面试指南》“遍历二叉树的神级方法”题目。 题目 给定一棵二叉树的头节点 head,完成二叉树的先序、中序和后序遍历。如果二叉树的节点数为N,则要求时间复杂度为O(N),额外空间复杂度为O(1)。 题解 之前的题目已经剖析过如何用递归和非递归的方法实现遍历二叉树,但是很不幸,之前所有的方法虽然常用,但都无法做到额外空间复杂度为O(1)。这是因为遍历二叉树的递归方
左神算法:遍历二叉树的神级方法(Morris遍历 / 线索二叉树)
本题来自左神《程序员代码面试指南》“遍历二叉树的神级方法”题目。 题目 给定一棵二叉树的头节点 head,完成二叉树的先序、中序和后序遍历。如果二叉树的节点数为N,则要求时间复杂度为O(N),额外空间复杂度为O(1)。 题解 之前的题目已经剖析过如何用递归和非递归的方法实现遍历二叉树,但是很不幸,之前所有的方法虽然常用,但都无法做到额外空间复杂度为O(1)。这是因为遍历二叉树的递归方







![[算法系列之十四]字符串匹配之Morris-Pratt字符串搜索算法](https://img-blog.csdn.net/20150206095023392)







